Wie kodierst du einen Text mit möglichst wenigen Bits? Brauchst du nicht für jeden Buchstaben gleich viele Bits? Normalerweise ja, wenn du eine Standardkodierung wie UTF-8 verwendest. Aber wenn du es auf Datenkompression anlegst, kodierst du häufig vorkommende Buchstaben wie das e mit wenigen Bits und seltenere Buchstaben wie das q dafür mit ein paar mehr Bits. So die Idee – systematisch umgesetzt wird sie beim Huffman-Code.
Idee
Die Idee, häufig vorkommende Buchstaben durch möglichst kurze Codewörter zu kodieren, ist auch beim Morse-Code verwirklicht. Der Buchstabe e wird durch ein Codewort der Länge 1, nämlich einen · kodiert, das Zeichen q wird dagegen durch ein Codewort der Länge 4, nämlich – – · – kodiert.
Bei Codes mit unterschiedlichen Codewortlängen aber kann es vorkommen, dass eine eindeutige Dekodierung von Zeichenfolgen nicht möglich ist. Im Morse-Code kannst du beispielsweise die Folge · · – · · · · – sowohl zu usa als auch idea dekodieren. Der Grund ist, dass manche Codewörter Anfangswörter von anderen Codewörtern sind. Du weißt dann nicht, wo ein Codewort endet und wo das nächste anfängt. Die angegebene Folge könnte mit e (·) oder mit i (· ·) oder mit u (· · – ) oder sogar mit f (· · – ·) anfangen.
Wenn dagegen die folgende Bedingung erfüllt ist, dann kannst du kodierte Zeichenfolgen direkt und eindeutig dekodieren. Im Morse-Code wird die Bedingung dadurch erfüllt, dass hinter jedem Codewort eine kurze Pause als Trennzeichen eingefügt wird.
Wenn kein Codewort Anfangswort eines anderen Codewortes ist, dann ist jede kodierte Zeichenfolge eindeutig dekodierbar.
Dies ist die sogenannte Fano-Bedingung (nach R. Fano). Ziel des Verfahrens von D.A. Huffman ist die Konstruktion eines Codes, der die Fano-Bedingung erfüllt und der einen Text mit möglichst wenigen Bits kodiert.
Anwendung findet die Huffman-Kodierung nicht nur bei der Kompression von Texten, sondern auch in der Fax-Übertragung und im Bilddaten-Kompressionsverfahren JPEG.
Huffman-Baum konstruieren
In dem Verfahren konstruierst du zunächst einen binären Baum mit einer Knotenmarkierung. Später liest du an den Kanten dieses sogenannten Huffman-Baums den Huffman-Code ab.
Eingabe: Text
Ausgabe: Binärer Baum mit einer Knotenmarkierung
Methode:
Erzeuge für jedes Zeichen , das im Text vorkommt, einen Knoten und markiere den Knoten mit der Häufigkeit, mit der im Text vorkommt
Solange es mehr als einen Knoten gibt, zu dem keine Kante hinführt, wiederhole
suche zwei Knoten und mit minimaler Markierung, zu denen noch keine Kante hinführt
erzeuge einen neuen Knoten
verbinde mit und
markiere den Knoten mit der Summe der Markierungen von und
Beispiel
Du möchtest zu dem Text abrakadabra den Huffman-Baum konstruieren.
Im folgenden Bild 1 siehst du die Situation nach Schritt 1 des Verfahrens. Die darauf folgenden Bilder 2 bis 4 zeigen weitere Stadien der Konstruktion des Baumes nach Schritt 2.
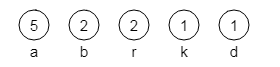
Bild 1: In Schritt 1 erzeugte Knoten
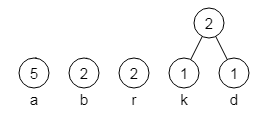
Bild 2: Der erste in Schritt 2 neu erzeugte Knoten
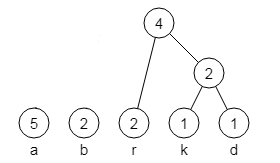
Bild 3: Der nächste in Schritt 2 neu erzeugte Knoten
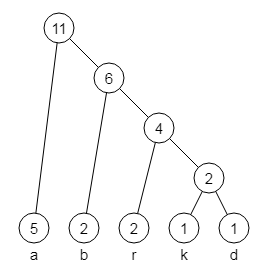
Bild 4: Der fertige Huffman-Baum
Das Verfahren zur Konstruktion des Huffman-Baums ist ein Beispiel für die Anwendung der Greedy-Strategie. Du wählst immer zwei Knoten mit minimaler Markierung aus – egal welche, wenn es mehrere Möglichkeiten gibt. Du erhältst in jedem Fall ein richtiges Ergebnis.
Huffman-Code erzeugen
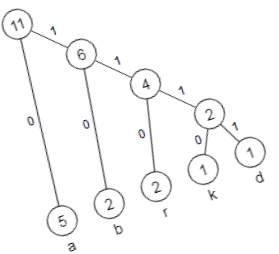
Du markierst nun die Kanten des Baumes mit 0 und 1, wie im folgenden Bild 5 zu sehen. Wenn du dann die Wege von der Wurzel zu den Blättern verfolgst, erhältst du die Codewörter des Huffman-Codes, also 0 für a, 10 für b, 110 für r, 1110 für k und 1111 für d.
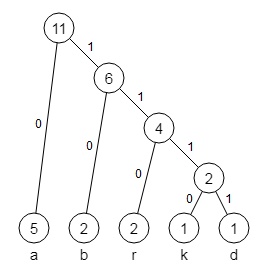
Bild 5: Kantenmarkierungen des Huffman-Baumes
Die Kodierung des gesamten Textes abrakadabra lautet somit: 01011001110011110101100. Die Länge der Kodierung beträgt 23 Bit.
Selber ausprobieren
Probiere am besten einmal selber aus, für einen (kurzen) Text, den du dir selber ausgedacht hast, den Huffman-Code zu konstruieren:
Kodierten Text wieder dekodieren
Wenn du diese Folge von Nullen und Einsen wieder dekodierst, woher weißt du dann, wo die Kodierung eines Buchstabens zu Ende ist und wo die nächste anfängt? Hier kommt die Fano-Bedingung ins Spiel: Kein Codewort ist Anfangswort eines anderen Codewortes! Wenn du also die erste Ziffer 0 liest, hast du den Buchstaben a schon erkannt! Und mit den folgenden Ziffern 10 das b!
Praktisch dekodierst du die Bitfolge 01011001110011110101100, indem du den Huffman-Baum von der Wurzel aus jeweils abhängig vom nächsten Bit durchläufst. Wenn du ein Blatt erreichst, gibst du den zugehörigen Buchstaben aus.
Mit dem ersten Bit 0 der Bitfolge landest du gleich bei einem Blatt und gibst das a aus.
Anschließend startest du wieder bei der Wurzel. Mit den folgenden Bits 10 erreichst du wieder ein Blatt und gibst das b aus.
Dann startest du wieder bei der Wurzel und erreichst mit den folgenden Bits 110 das Blatt mit dem Buchstaben r.
Und so weiter…
Der Huffman-Code ist optimal
Der Huffman-Code ist optimal – kürzer kannst du einen Text nicht kodieren, wenn du ihn zeichenweise kodierst.
Der Informationsgehalt eines Textes beträgt
Bit
wobei die Länge des Textes ist und die Wahrscheinlichkeit, mit der das -te Textzeichen im Text auftritt (Auftreten als unabhängige Ereignisse aufgefasst).
Der Text abrakadabra hat die Länge 11, die Auftretenswahrscheinlichkeiten betragen , , , usw.
In folgender Tabelle ist der Text abrakadabra mit den Auftretenswahrscheinlichkeiten der einzelnen Buchstaben dargestellt, beispielsweise . Darunter sind deren Logarithmen angegeben und rechts davon die Summe der Logarithmen. Die negative Summe 22,4 stellt den Informationsgehalt in Bit des Textes abrakadabra dar.
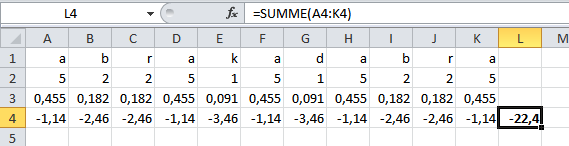
Mit den 23 Bit der Huffman-Kodierung hast du damit das Optimum erzielt, denn 22 Bit reichen nicht für den Informationsgehalt von 22,4 Bit.
Wenn du dir dagegen für die 5 verschiedenen Buchstaben des Textes einen 3-Bit-Blockcode ausgedacht hättest, so hättest du für die Codierung des Textes abrakadabra 11·3 Bit = 33 Bit benötigt.
Bei der Übertragung von Huffman-kodierten Texten muss im Allgemeinen die Code-Tabelle mit übertragen werden, was sich natürlich nur bei längeren Texten lohnt. Die Kompressionsrate ist stark von der Wahrscheinlichkeitsverteilung der Zeichen abhängig.
