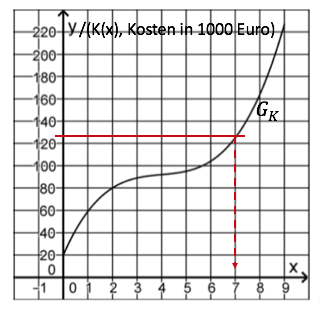
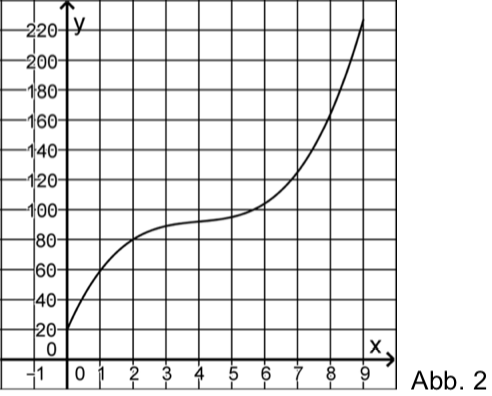
Die Kosten, die einem Unternehmen bei der Herstellung einer Flüssigkeit entstehen, können durch die Funktion K:x↦x3−12x2+50x+20 mit x∈[0;9] beschrieben werden. Dabei gibt K(x) die Kosten in 1000 Euro an, die bei der Produktion von x Kubikmetern der Flüssigkeit insgesamt entstehen. Abbildung 2 zeigt den Graphen von K.
a) 3 BE
Geben Sie mit Hilfe von Abbildung 2
die Produktionsmenge an, bei der die Kosten 125000 Euro betragen.
das Monotonieverhalten von K an und deuten Sie Ihre Angabe im Sachzusammenhang.
Die Funktion E mit E(x)=23x gibt für 0≤x≤9 den Erlös (in 1000 Euro) an, den das Unternehmen beim Verkauf von x Kubikmetern der Flüssigkeit erzielt. Für die sogenannte Gewinnfunktion G gilt G(x)=E(x)−K(x). Positive Werte von G werden als Gewinn bezeichnet, negative als Verlust.
b) 2 BE
Zeigen Sie, dass das Unternehmen keinen Gewinn erzielt, wenn vier Kubikmeter der Flüssigkeit verkauft werden.
c) 3 BE
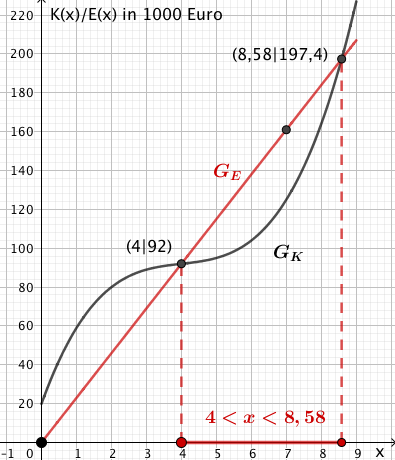
Zeichnen Sie den Graphen von E in Abbildung 2 ein. Bestimmen Sie mithilfe der so entstehenden Darstellung den Bereich, in dem die verkaufte Menge der Flüssigkeit liegen muss, damit das Unternehmen einen Gewinn erzielt.
d) 5 BE
Berechnen Sie, welche Menge der Flüssigkeit verkauft werden muss, damit das Unternehmen den größten Gewinn erzielt.
Bei der Aufgabe ist die Gewinnfunktion beim Verkauf eines Produktes zu untersuchen. Gegeben sind der Funktionsterm einer ganzrationalen Funktion 3. Grades und ihr Graph sowie der Funktionsterm der linearen Erlösfunktion.
Lösung Teilaufgabe a)
Ziehe in Höhe von y=125 (wähle die Stelle auf der y-Achse möglichst genau) die Parallele zur x-Achse. Sie schneidet GK im Punkt (7∣125).
Bei einer Produktionmenge von ca. 7 Kubikmetern betragen die Herstellungskosten also 125000 Euro.
Dies bedeutet, dass die Produktionskosten mit der Menge an produzierter Flüssigkeit zunehmen.
Die Zunahme ist im Intervall [3;5] vergleichsweise gering, da K offenbar für x=4 einen Wendepunkt besitzt.
Lösung Teilaufgabe b)
Kostenfunktion:
K(x)=x3−12x2+50x+20 mit x∈[0;9]
Erlösfunktion:
E(x)=23x mit x∈[0;9]
Gewinnfunktion:
G(x)=E(x)−K(x)Setze die Funktionsterme ein und fasse zusammen:
G(x)=−x3+12x2−27x−20x∈[0;9]
Berechne G(x) für x=4:
G(4)=−64+12⋅16−108−20=0
Also wird kein Gewinn erzielt, wenn das Unternehmen vier Kubikmeter der Flüssigkeit verkauft.
Lösung Teilaufgabe c)
Den geradlinigen Graphen der Funktion E zeichnest du am besten mit dem Punkt (0∣0) und dem Punkt (7∣161). Der erste lässt sich ja korrekt eintragen, der zweite mit geringer Ungenauigkeit auch.
Das Unternehmen erzielt einen Gewinn, wenn der Erlös größer ist als die Kosten.
Dazu muss gelten:
E(x)>K(x).
Nun kannst du aus der Skizze ablesen, dass x näherungsweise in folgendem Bereich liegt:
4<x<8,5.
Damit das Unternehmen einen Gewinn erzielt, muss die verkaufte Menge der Flüssigkeit zwischen 4 und ca. 8,5 Kubikmetern liegen.
Lösung Teilaufgabe d)
Hier ist das Maximum der Gewinnfunktion G im Intervall ]4;8,5[ zu berechnen. Ein lokales Maximum bestimmt Du über die Nullstellen der Ableitung von G.
x2 ist die Lösung, die in unserem Intervall liegt, und damit das gesuchte Maximum. Die Firma macht also bei einem Verkauf von 6,65 Kubikmetern der Flüssigkeit am meisten Gewinn.
Um sicher zu gehen, dass es sich um das Maximum und nicht ein Minimum handelt, musst du noch die zweite Ableitung ausrechnen und den x-Wert einsetzen.
G′′(x)=−6x+24
Setze x=6,65 ein.
G′′(6,65)=−15,9
Damit handelt es sich bei dem gefundenen Wert tatsächlich um ein Maximum.
