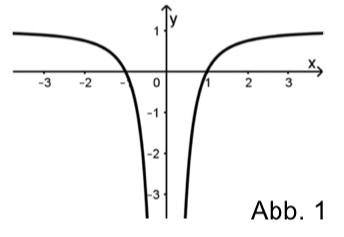
Im Zusammenhang mit einer gegebenen gebrochen-rationalen Funktion ist ein Flächenstück zu berechnen.

Lösung Teilaufgabe a)

In dieser Teilaufgabe sind die beiden Funktionen

$f:x\mapsto1-\frac{1}{x^2}$ und

$g:x\mapsto-3$

zu schneiden.

Setze die beiden Funktionsterme gleich und löse die Gleichung.

$\def\arraystretch{1.25} \begin{array}{rcll}\displaystyle1-\frac{1}{x^2}&=&-3&|\;\cdot x^2\\x^2-1&=&-3x^2&|\;+3x^2+1\\4x^2&=&1&|\;:4\\x^2&=&\displaystyle \frac{1}{4}&|\;\sqrt{}\\x_1&=&\displaystyle +\frac12\\x_2&=&-\displaystyle \frac12 \end{array}$

Einer der beiden Schnittpunkte der Graphen von $f$ und $g$ ist der Punkt $S(0{,}5|-3)$.

Lösung Teilaufgabe b)

Die Teilaufgabe verlangt eine Flächenberechnung.

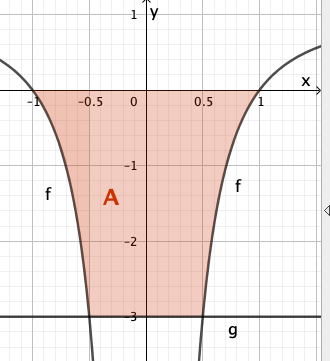
Schraffiere zunächst die zu berechnende Fläche in einer Skizze.

Achtung:

Gemeint ist eine Fläche, deren Rand allein aus Teilen des Graphen von $f$, aus Teilen der x-Achse und Teilen des Graphen von $g$ besteht.

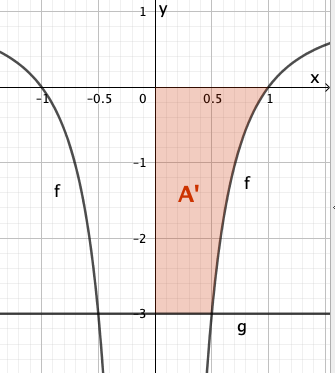
Die Fläche $A'$ ist deshalb nicht die richtige Fläche, da ihr Rand einen Teil der y-Achse enthält.

Dennoch ist $A'$ hilfreich zur Berechnung der Fläche $A$, da - wegen der Symmetrie des Graphen von $f$ zur y-Achse - gilt: $A=2\cdot A'$.

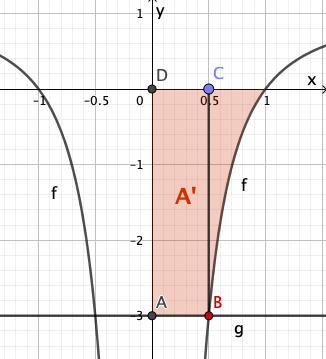
So berechnest du die Fläche $A'$:

$\def\arraystretch{2} \begin{array}{rcll}A'&=&\text{Rechteck}_{ABCD}+\color{red}{|}\displaystyle \int_{0{,}5}^1f(x)\mathrm{dx}\,\color{red}{|}\\&=&\quad0{,}5\cdot 3 \quad\quad +|\,\displaystyle\int_{0{,}5}^1(1-\frac{1}{x^2})\mathrm{dx}\,|\end{array}$

$\def\arraystretch{1.25} \begin{array}{rcll}A'&=&\quad\quad1{,}5\quad\quad+|\,\big[x\color{red}{+x^{-1}}\big]_{0{,}5}^1\,|\\&=&\quad\quad1{,}5\quad+|(1+1)-(0{,}5+\color{red}{2})|\\&=&\quad\quad1{,}5\quad+\;\color{red}{0{,}5}\\A'&=&\quad\quad2\end{array}$

Damit gilt für die gesuchte Fläche der Teilaufgabe:

$A=4$