1.0 Gegeben ist die ganzrationale Funktion g dritten Grades mit $D_g=\mathbb{R}$, deren Graph $G_g$ in nebenstehender Abbildung dargestellt ist. Vom Graphen sind folgende Eigenschaften bekannt: $G_g$ hat bei der Nullstelle $x=6$ eine Tangente $G_t$ mit $t:y=16x-96$ mit $x\in\mathbb{R}$ und besitzt den Wendepunkt $W(5 |-18)$.

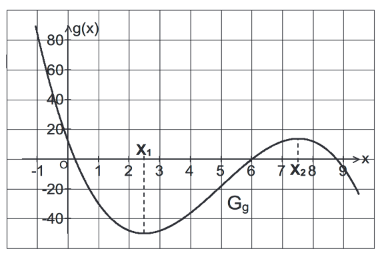
1.1 Skizzieren Sie den Graphen $G_g$ der 1. Ableitungsfunktion von g in ein geeignetes Koordinatensystem und geben Sie die max. Monotonieintervalle der 1. Ableitungsfunktion $g'$ an.

1.2.0 Zur Bestimmung des Funktionsterms g(x) ist folgendes Gleichungssystem gegeben:

$(I)$ $216a+36b+6c+d=0$

$(II)$ $125a+25b+5c+d=-18$

$III)$ $108a+12b+c=16$

$(IV)$ $30a+2b=0$

1.2.1 Geben Sie nachvollziehbar an, welche Ansätze zu diesen Gleichungen führen.

1.2.2 Bestimmen Sie g(x) mithilfe der Gleichungen aus 1.2.0.