A I

1.0 Gegeben ist die ganzrationale Funktion g dritten Grades mit $D_g=\mathbb{R}$, deren Graph $G_g$ in nebenstehender Abbildung dargestellt ist. Vom Graphen sind folgende Eigenschaften bekannt: $G_g$ hat bei der Nullstelle $x=6$ eine Tangente $G_t$ mit $t:y=16x-96$ mit $x\in\mathbb{R}$ und besitzt den Wendepunkt $W(5 |-18)$.

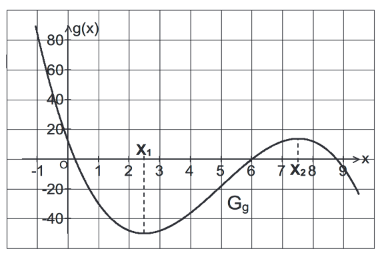
1.1 Skizzieren Sie den Graphen $G_g$ der 1. Ableitungsfunktion von g in ein geeignetes Koordinatensystem und geben Sie die max. Monotonieintervalle der 1. Ableitungsfunktion $g'$ an.

1.2.0 Zur Bestimmung des Funktionsterms g(x) ist folgendes Gleichungssystem gegeben:

$(I)$ $216a+36b+6c+d=0$

$(II)$ $125a+25b+5c+d=-18$

$III)$ $108a+12b+c=16$

$(IV)$ $30a+2b=0$

1.2.1 Geben Sie nachvollziehbar an, welche Ansätze zu diesen Gleichungen führen.

1.2.2 Bestimmen Sie g(x) mithilfe der Gleichungen aus 1.2.0.

2.0 Gegeben ist nun die Funktion $f:=x\mapsto\frac1{10}\cdot g(x)=\frac1{10}(-x^3+15x^2-56x+12)$mit $D_f=\mathbb{R}$, wobei g die Funktion aus Teilaufgabe $1.2.2$ ist. Der Graph wird mit $G_f$ bezeichnet.

2.1 Berechnen Sie alle Schnittpunkte des Graphen $G_f$ mit den Koordinatenachsen.

2.2 Ermitteln Sie Art und Koordinaten aller relativen Extrempunkte von $G_f$. Runden Sie die Koordinaten auf eine Nachkommastelle.

2.3 Bestimmen Sie die maximalen Krümmungsintervalle von $G_f$.

2.4 Zeichnen Sie unter Mitverwendung vorliegender Ergebnisse den Graphen $G_f$ im Bereich $-1\leqslant x\leqslant10$ in ein kartesisches Koordinatensystem.

Maßstab: $1$ LE $= 1cm$.

2.5 Es gilt $\int_{-2}^6f(x)dx=0$. Interpretieren Sie dieses Ergebnis in Bezug auf $G_f$.

2.6 Die Parabel $G_p$ mit $p(x)=-0{,}1x^2+0{,}4x+1{,}2$ und $D_p=\mathbb{R}$ schließt mit $G_f$ im I. und IV. Quadranten zwei endliche Flächenstücke ein. Zeichnen Sie $G_p$ für $-1\leqslant x\leqslant10$ in das vorhandene Koordinatensystem ein, schraffieren Sie das linke der beiden Flächenstücke und berechnen Sie die Maßzahl seines Flächeninhalts. Die Integrationsgrenzen können der Zeichnung entnommen werden.

3.0 Einer Halbkugel mit Radius $R=10cm$ soll ein Zylinder mit Radius $r$ und Höhe $h$ einbeschrieben werden (siehe Skizze). Bei Berechnungen kann auf die Verwendung von Einheiten verzichtet werden.

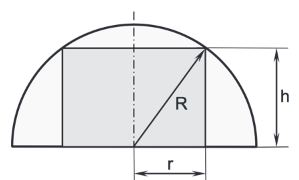
3.1 Ermitteln Sie die Maßzahl $V(h)$ des Volumens des Zylinders in Abhängigkeit von der Höhe $h$ und geben Sie eine sinnvolle Definitionsmenge für die Funktion $V:h\mapsto V(h)$ an, wenn die Höhe $h$ mindestens $6 cm$ betragen soll.

[Mögliches Teilergebnis: $V(h)=h\mathrm\pi(100-\mathrm h^2)$]

3.2 Berechnen Sie $h$ so, dass $V(h)$ den absolut größten Wert annimmt, und untersuchen Sie, ob das maximale Volumen $V_{max}$ des Zylinders mehr als die Hälfte des Halbkugelvolumens beträgt.