Eine Eisdiele lässt ein Logo für ihr Schaufenster anfertigen, das aus drei deckungsgleichen Figuren besteht. Berechne den Flächeninhalt dieses Logos.
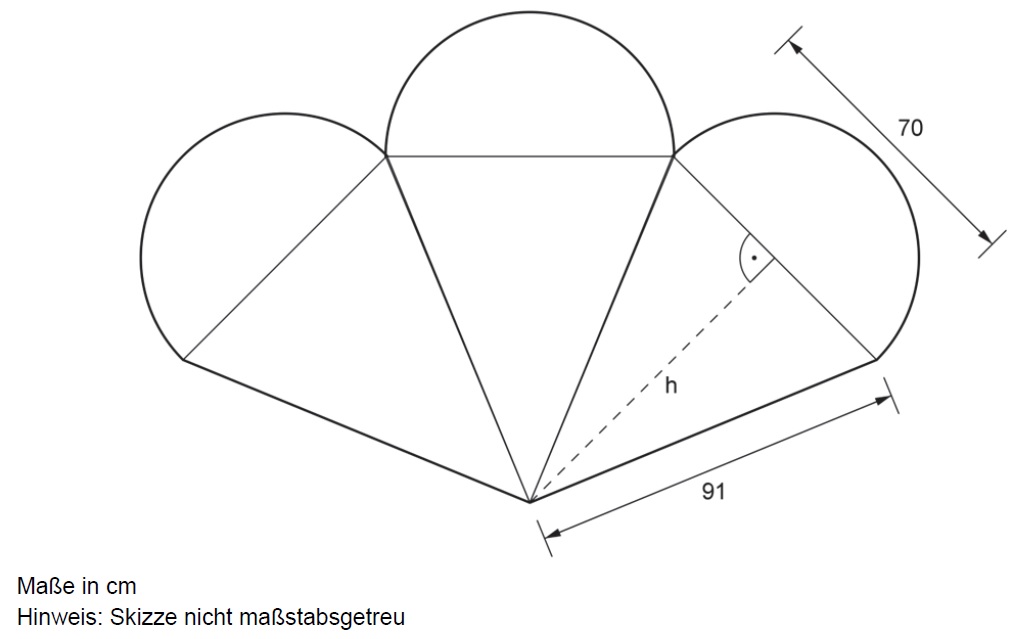
Eine Eisdiele lässt ein Logo für ihr Schaufenster anfertigen, das aus drei deckungsgleichen Figuren besteht. Berechne den Flächeninhalt dieses Logos.
