Die freie Lernplattform

Aufgaben zur Punktspiegelung

1
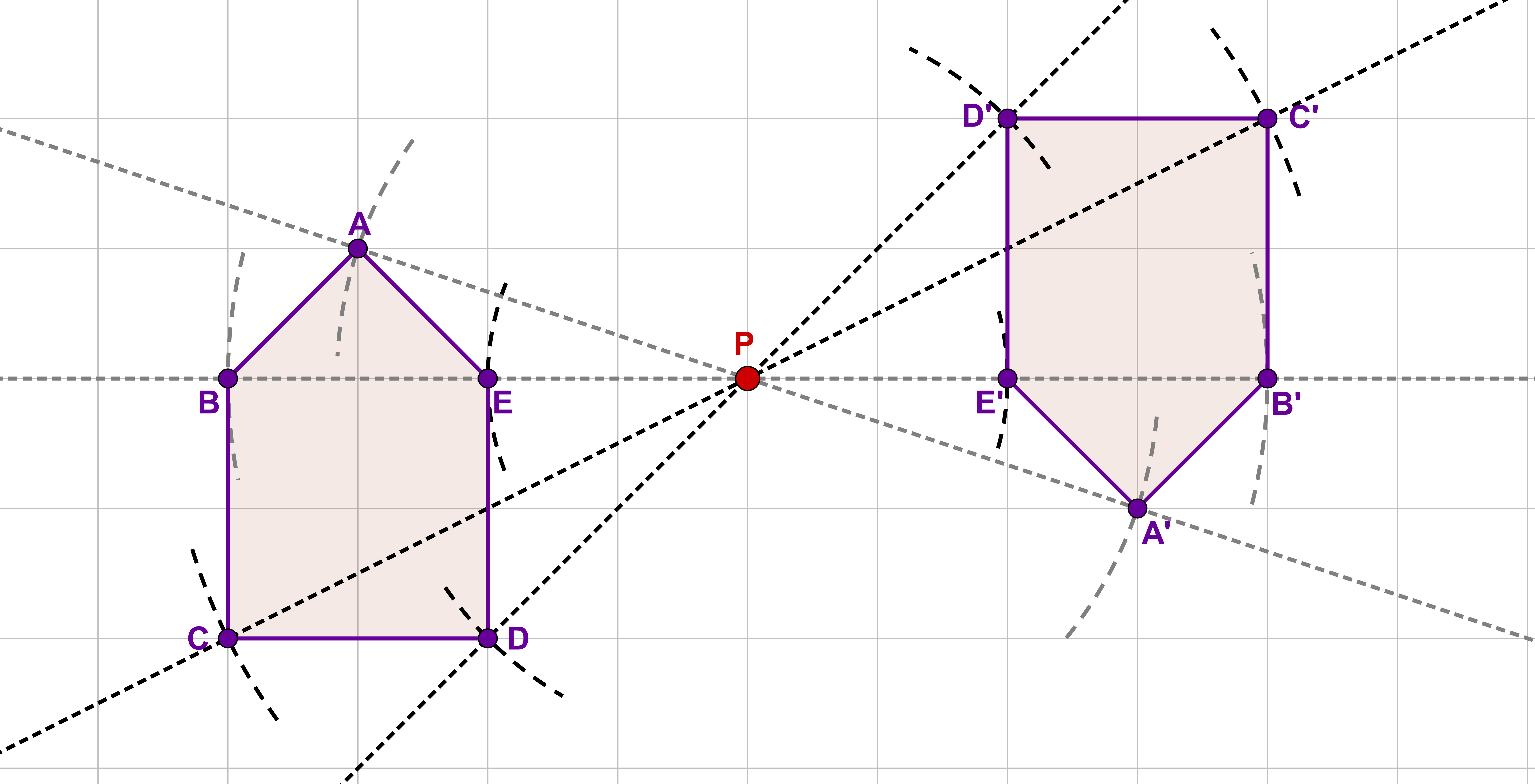
Übertrage die Figur und den Punkt $P$ in ein Gitternetz in deinem Heft. Spiegle dann die Figur an dem Punkt $P$ .
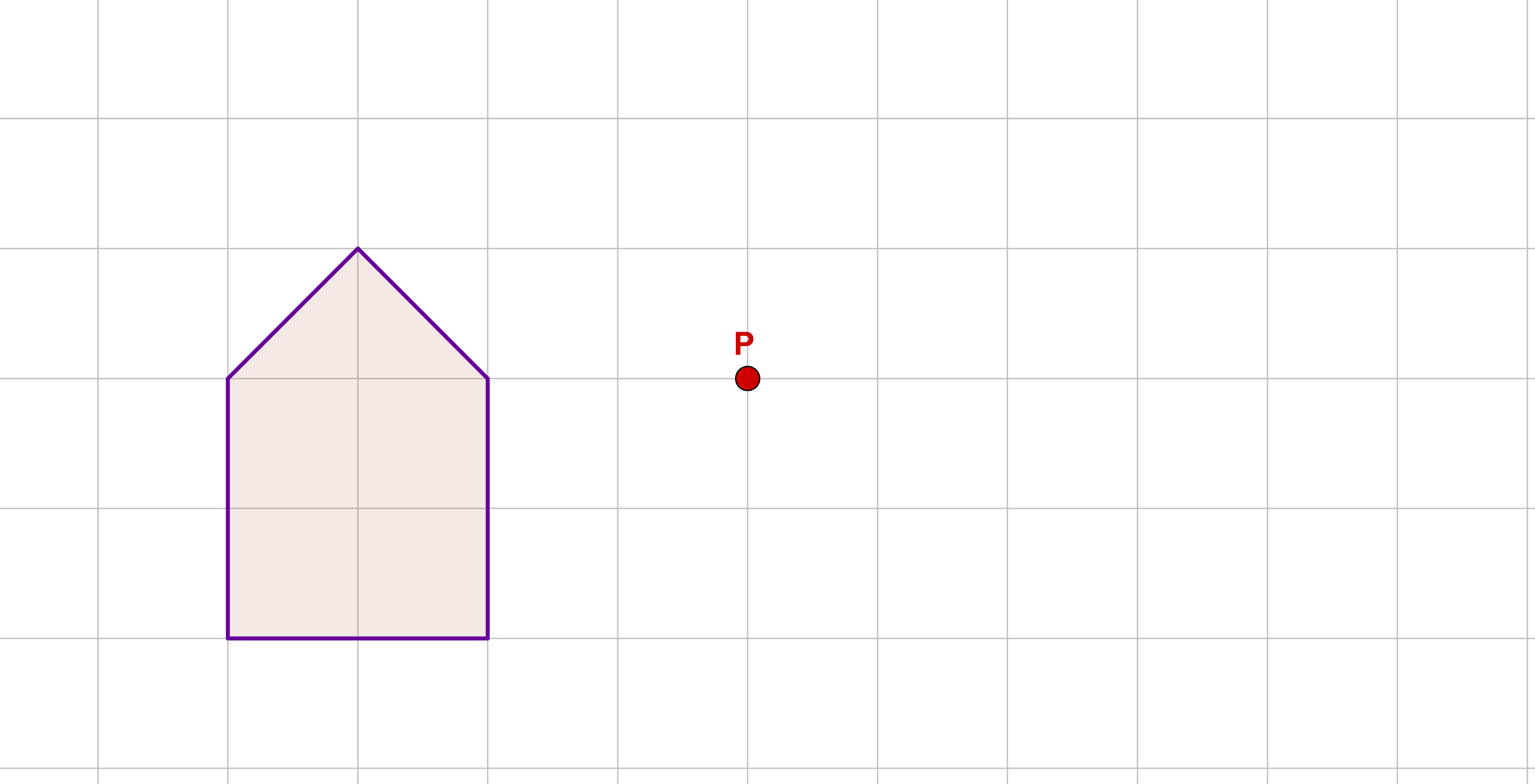
1. Für diese Aufgabe benötigst Du folgendes Grundwissen: Punktspiegelung
  Suche die charakteristischen Punkte in der Figur.
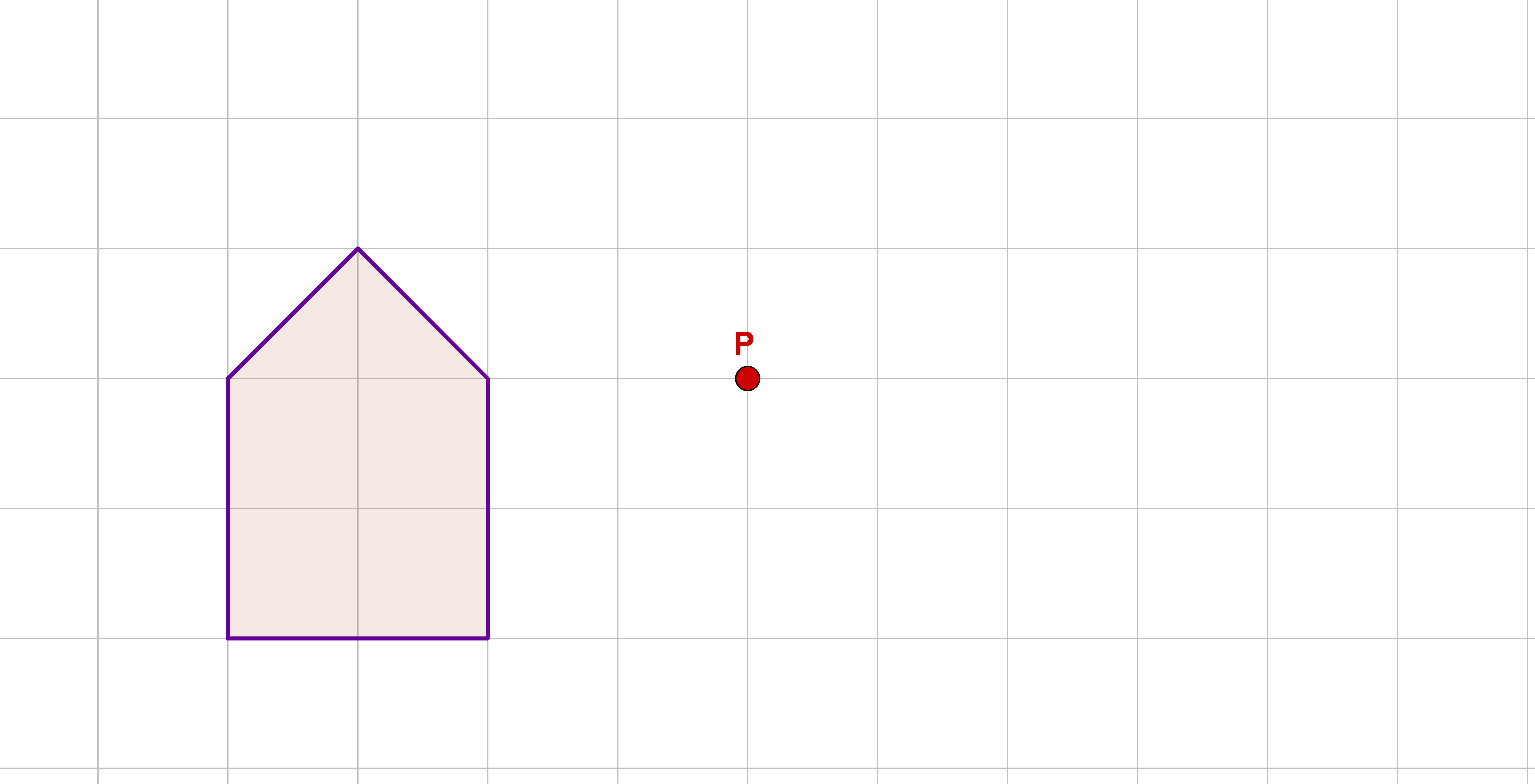
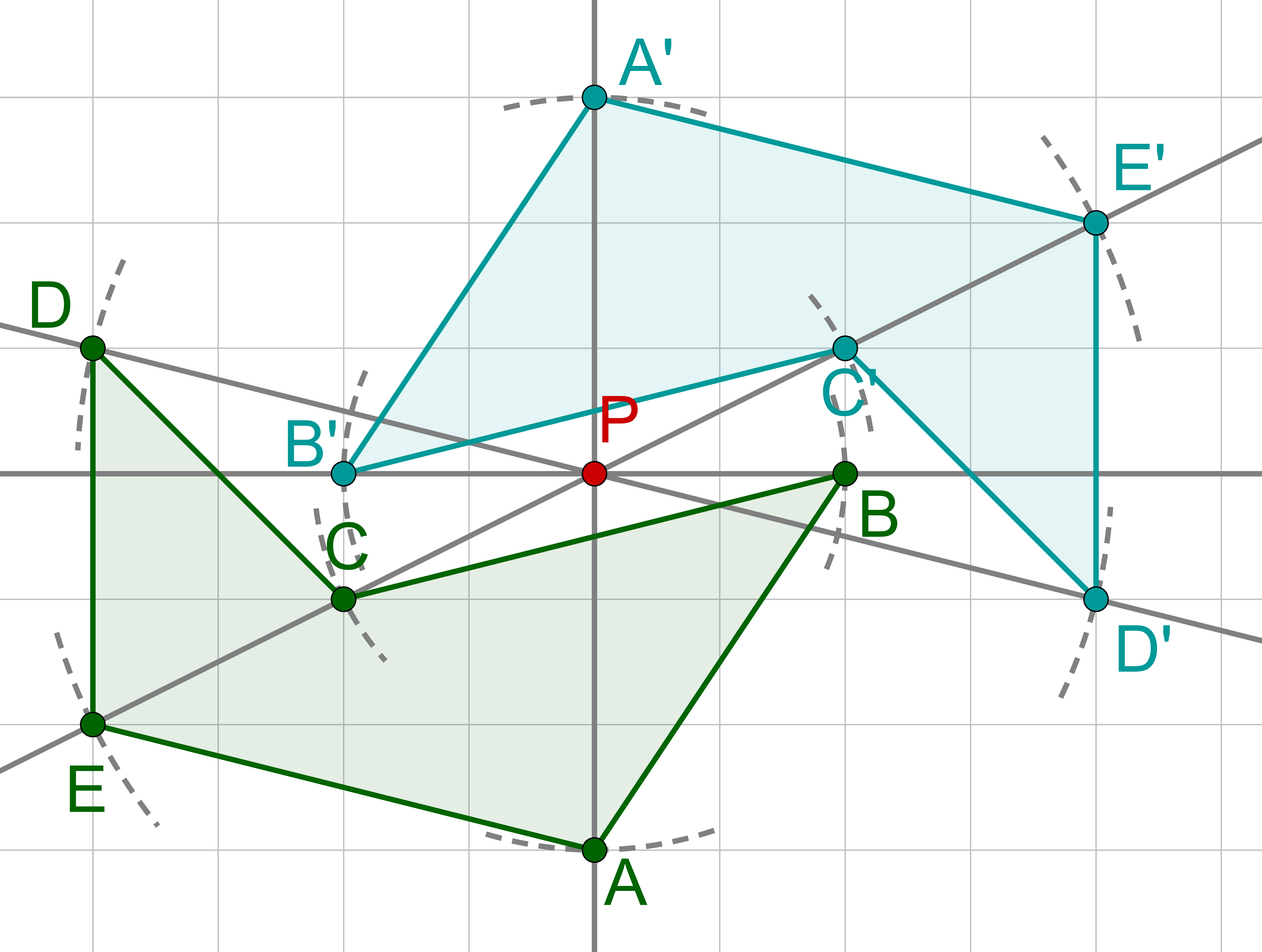
  Spiegle Punkt $A$ an $P$ indem du zuerst eine Gerade durch die Punkte $A$ und $P$ zeichnest.
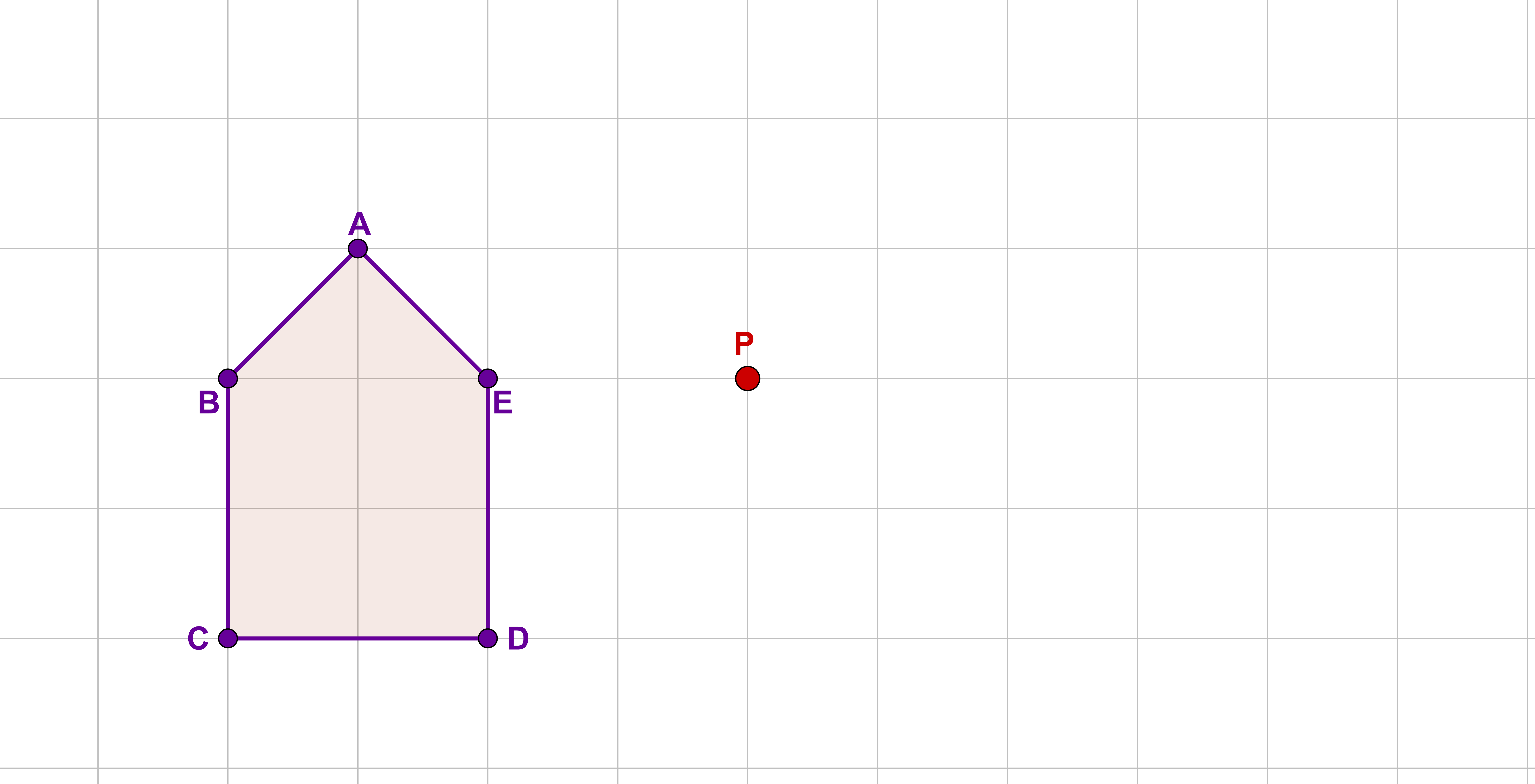
  Zeichne dir dann einen Hilfskreis um den Punkt $P$ mit Radius der Länge $[AP]$ . Der Schnittpunkt des Kreises mit der Geraden ist der Spiegelpunkt $A'$ .
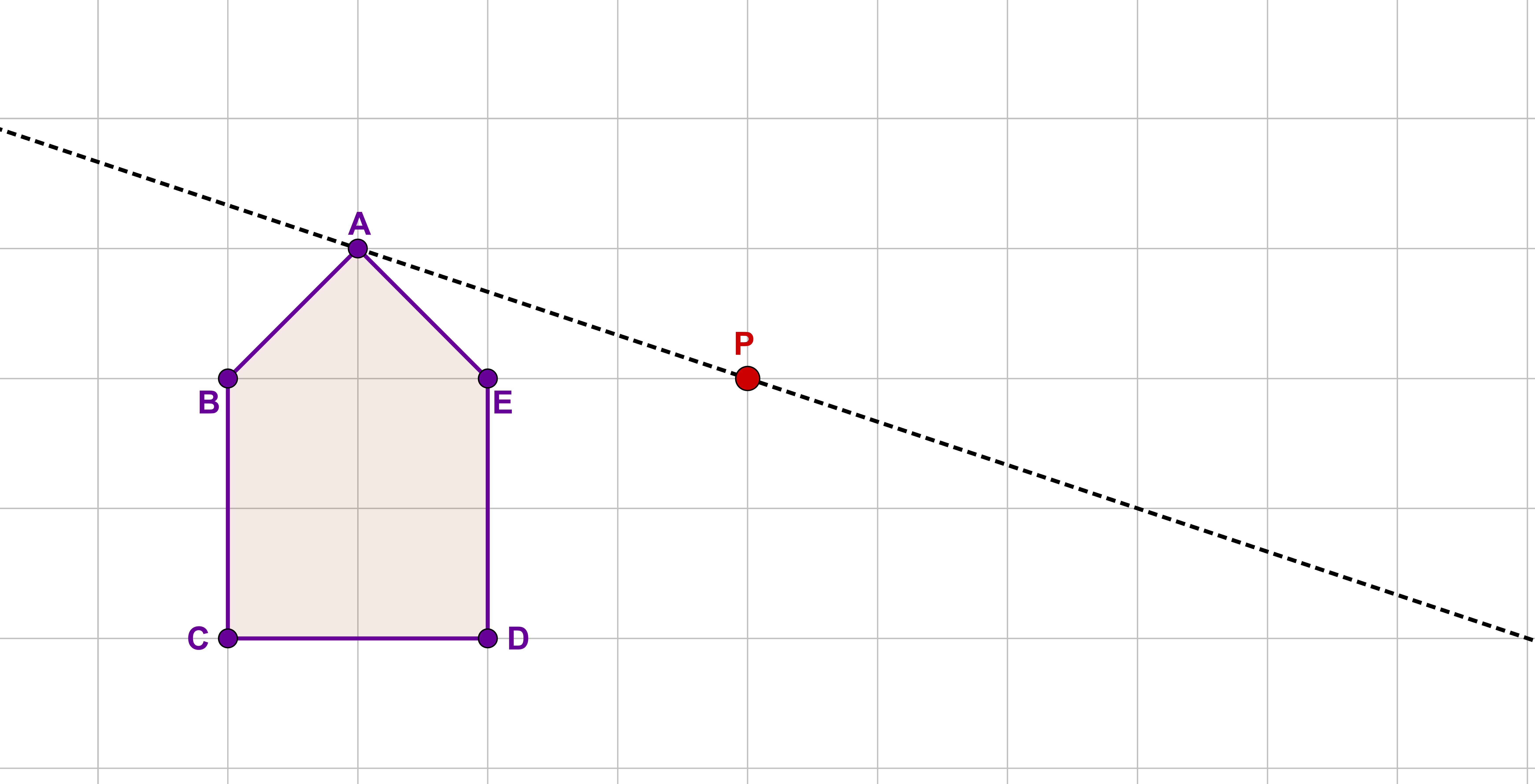
  Wähle nun den nächsten Punkt $B$ und zeichne eine Gerade durch die Punkte $B$ und $P$ .
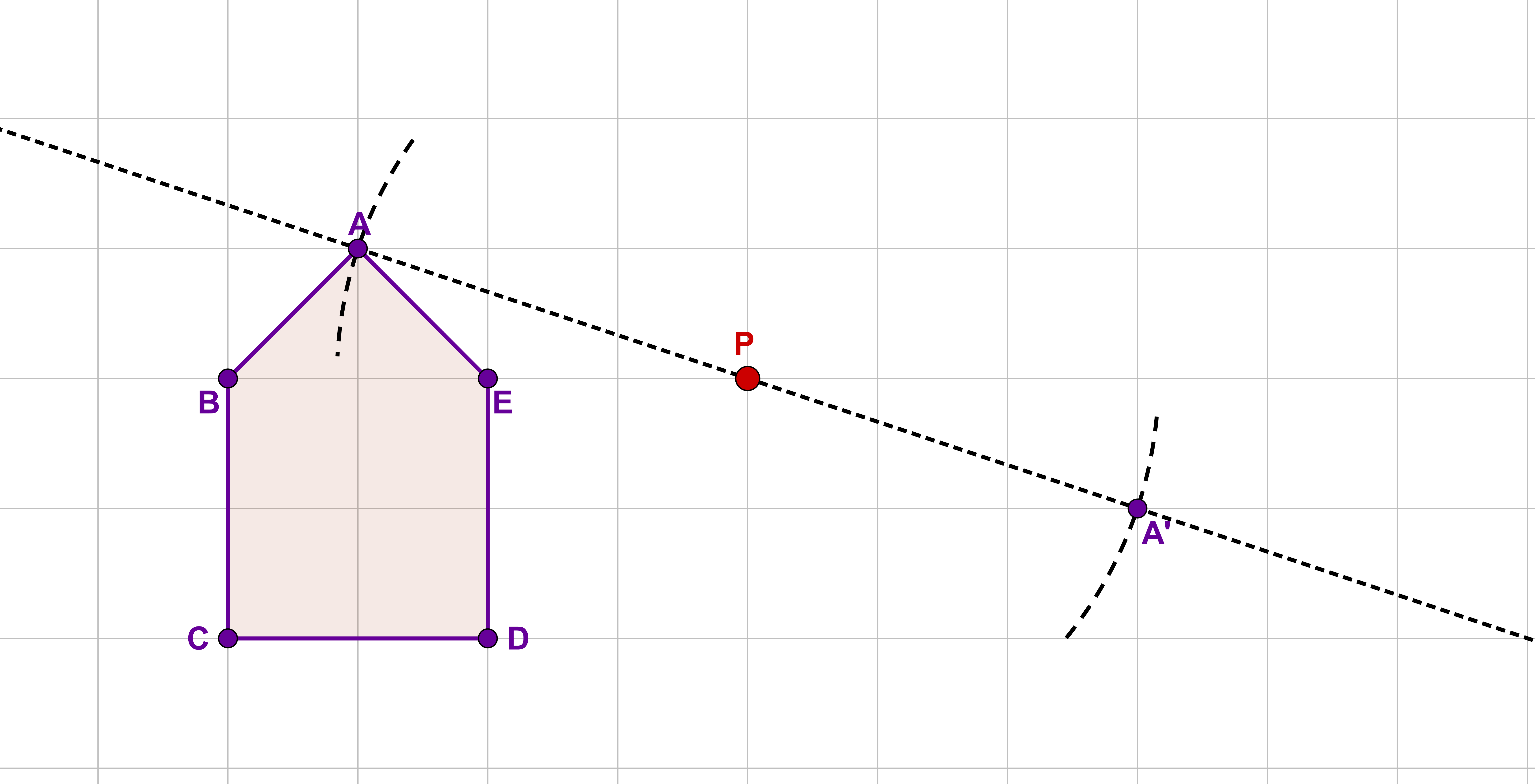
  Zeichne auch hier einen Hilfskreis mit dem Radius $[BP]$ um den Punkt $P$ . Der Schnittpunkt dieses Kreises mit der Geraden $BP$ ist der Spiegelpunkt $B'$ .
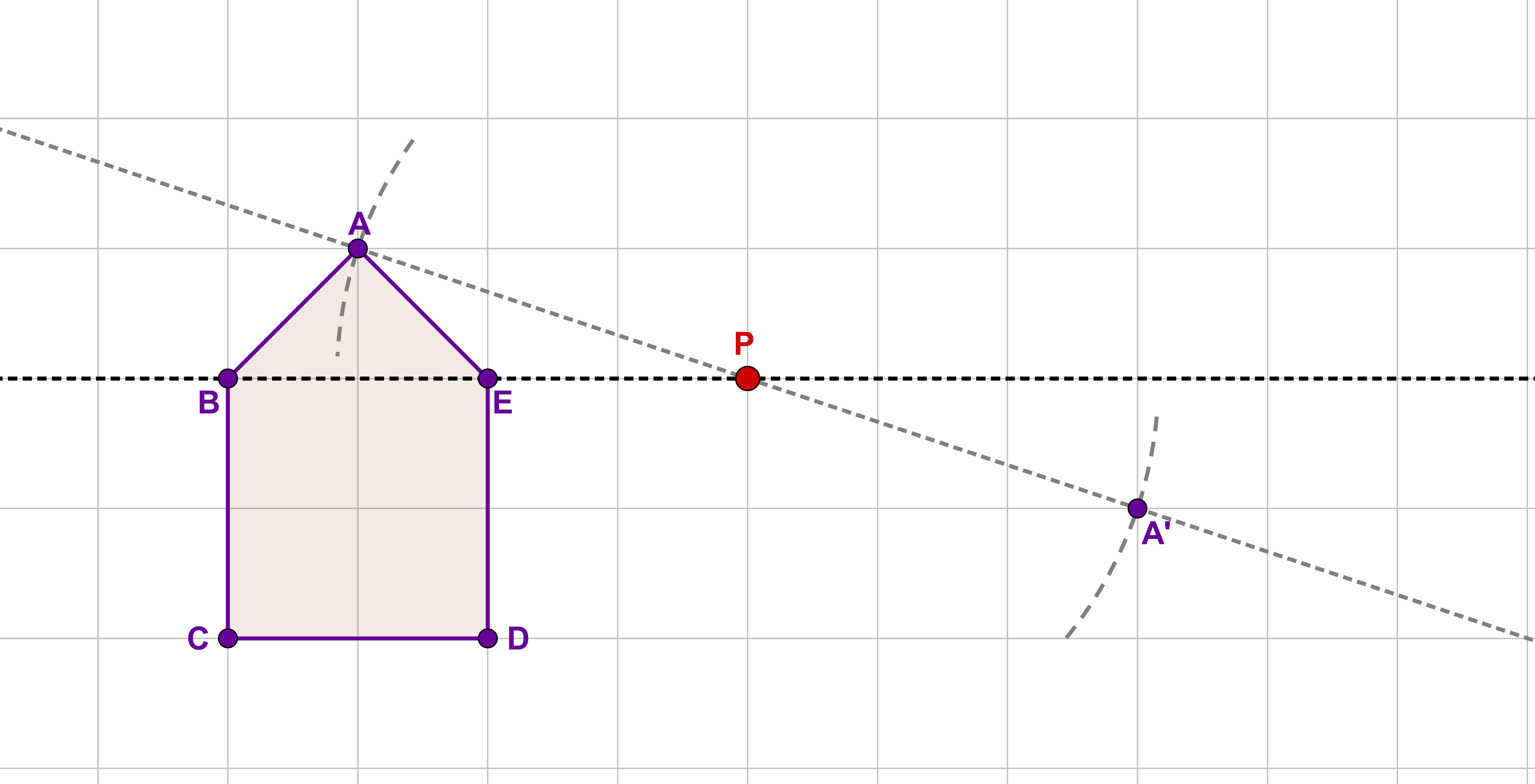
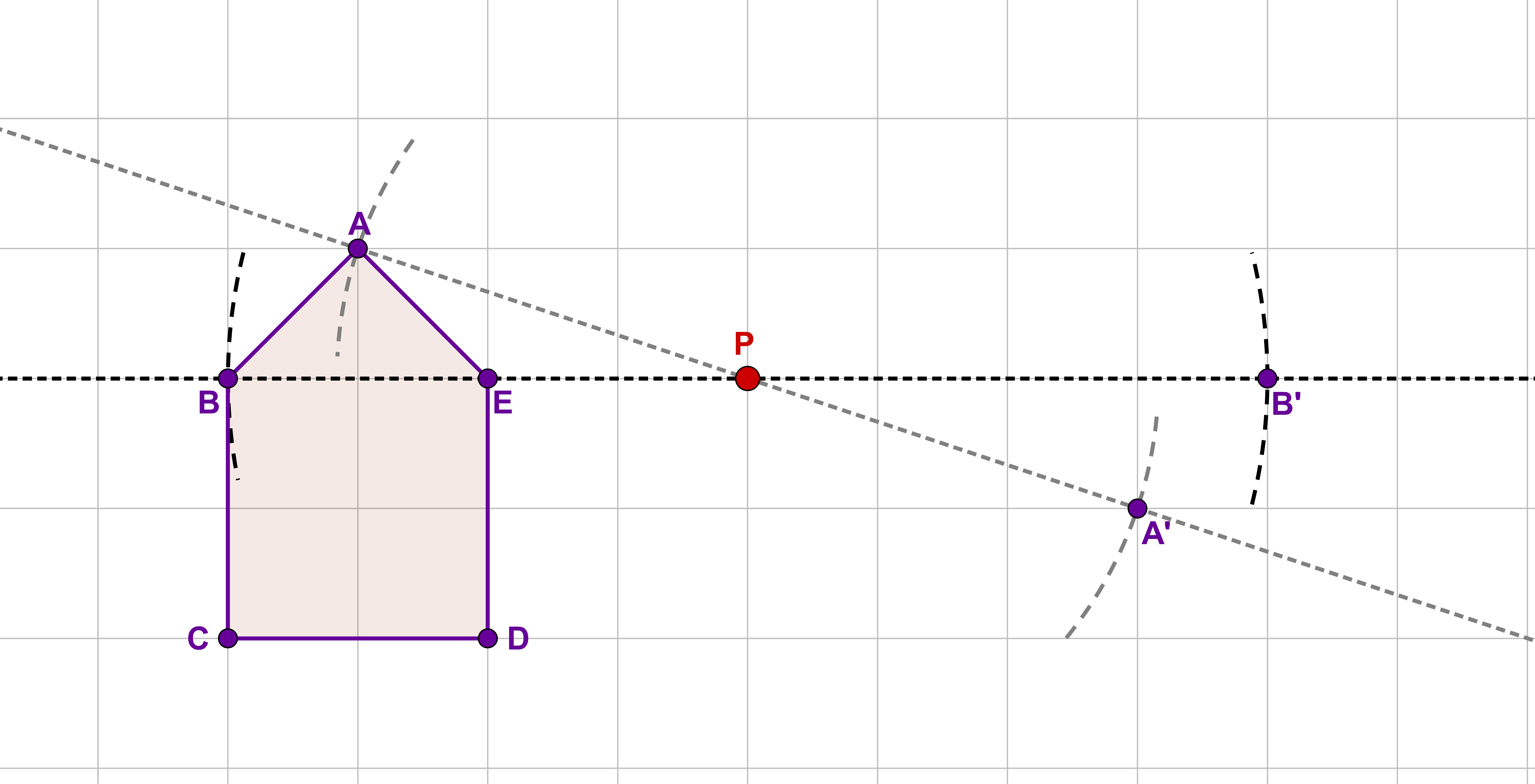
  Finde für alle weiteren charakteristischen Punkte die Geraden mit $P$ und die jeweiligen Hilfskreise um $P$ um die restlichen Spiegelpunkte der Figur zu erhalten.
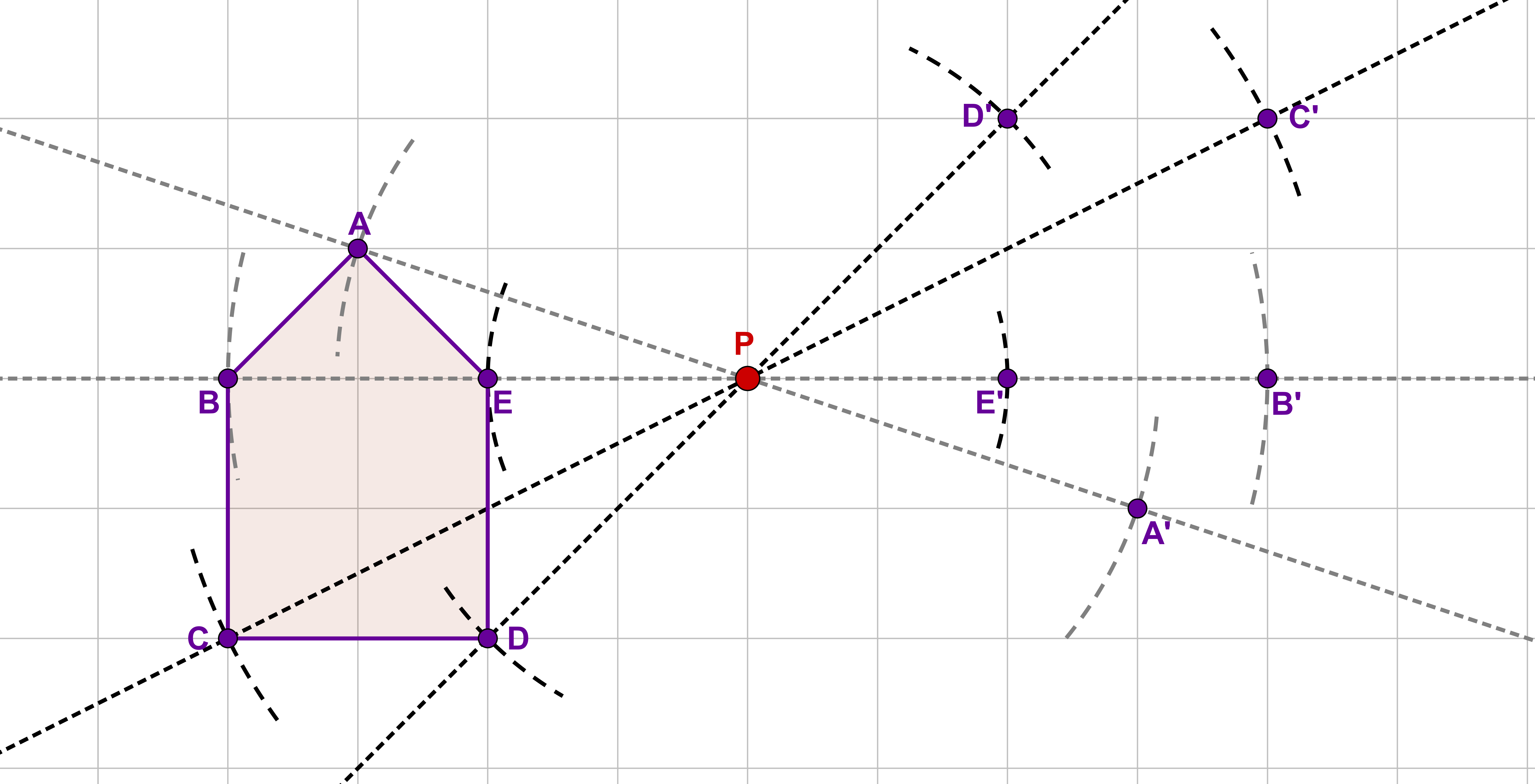
  Verbinde die Punkte in der richtigen Reihenfolge.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
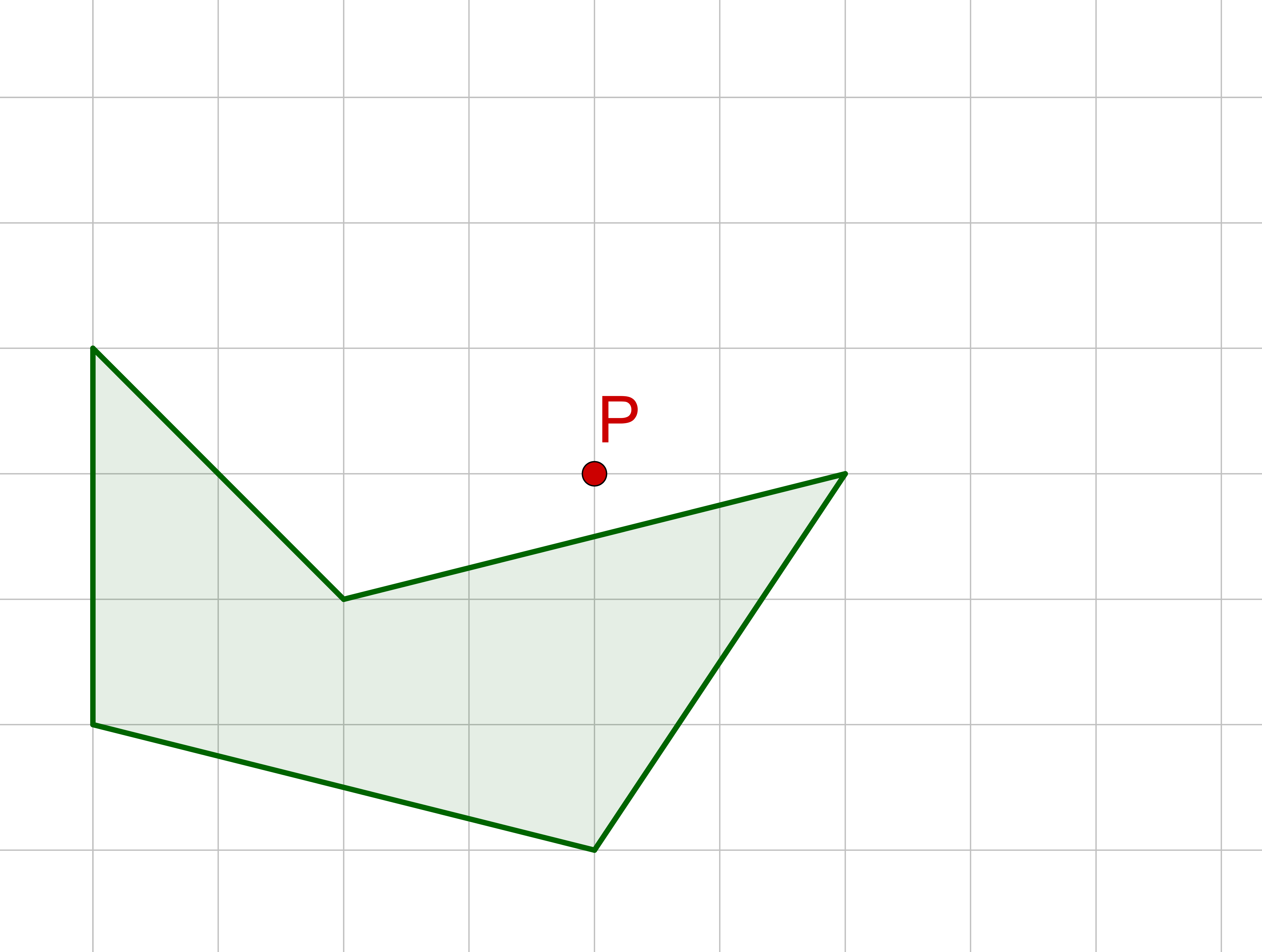
2. Für diese Aufgabe benötigst Du folgendes Grundwissen: Punktspiegelung
  Suche die charakteristischen Punkte der Figur.
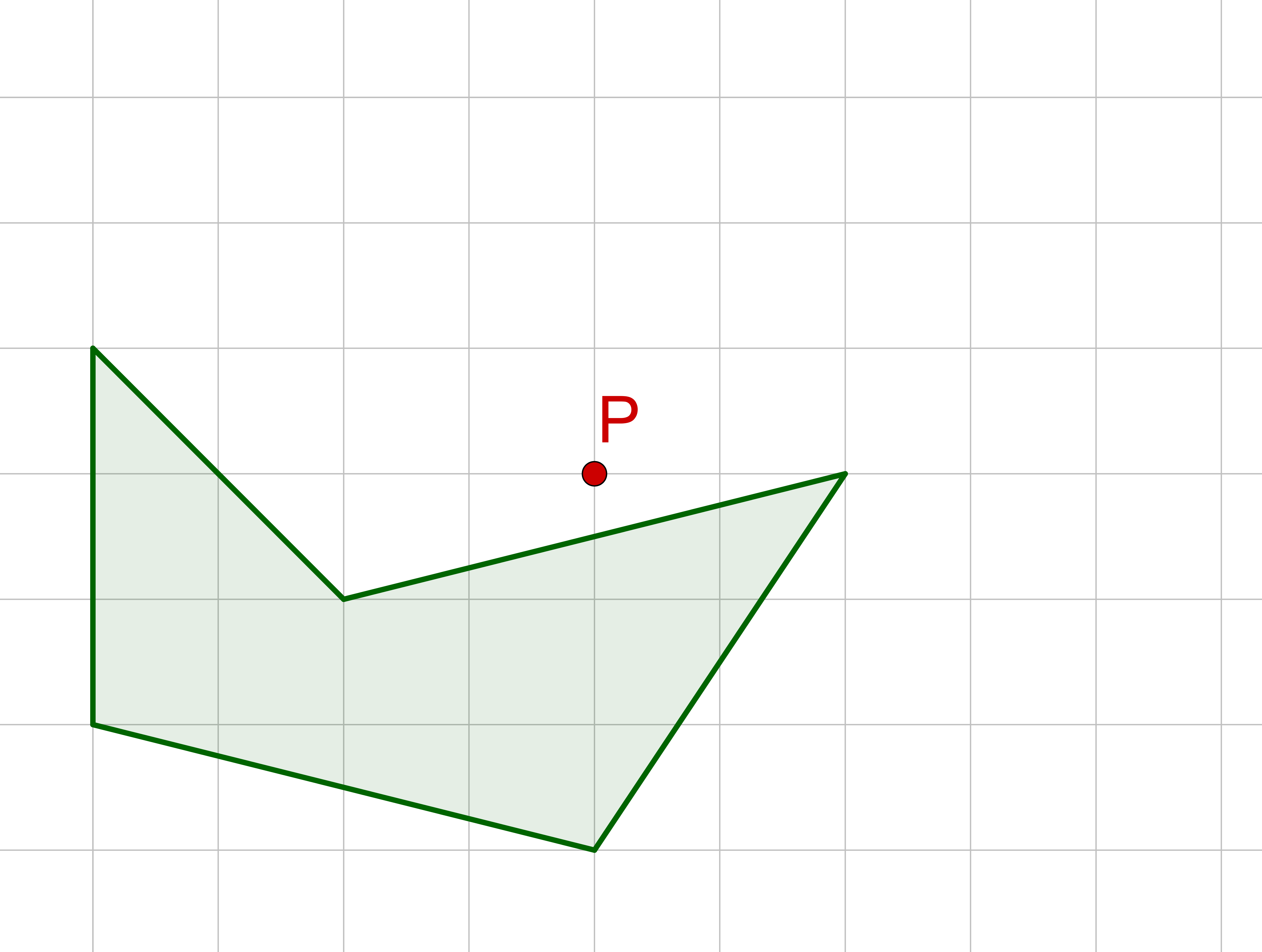
  Wähle Punkt $A$ und zeichne eine Gerade durch die Punkte $A$ und $P$ .
  Zeichne einen Kreis um $P$ mit Radius $[AP]$ . Der Schnittpunkt des Kreises mit der Geraden ist der Spiegelpunkt $A'$ .
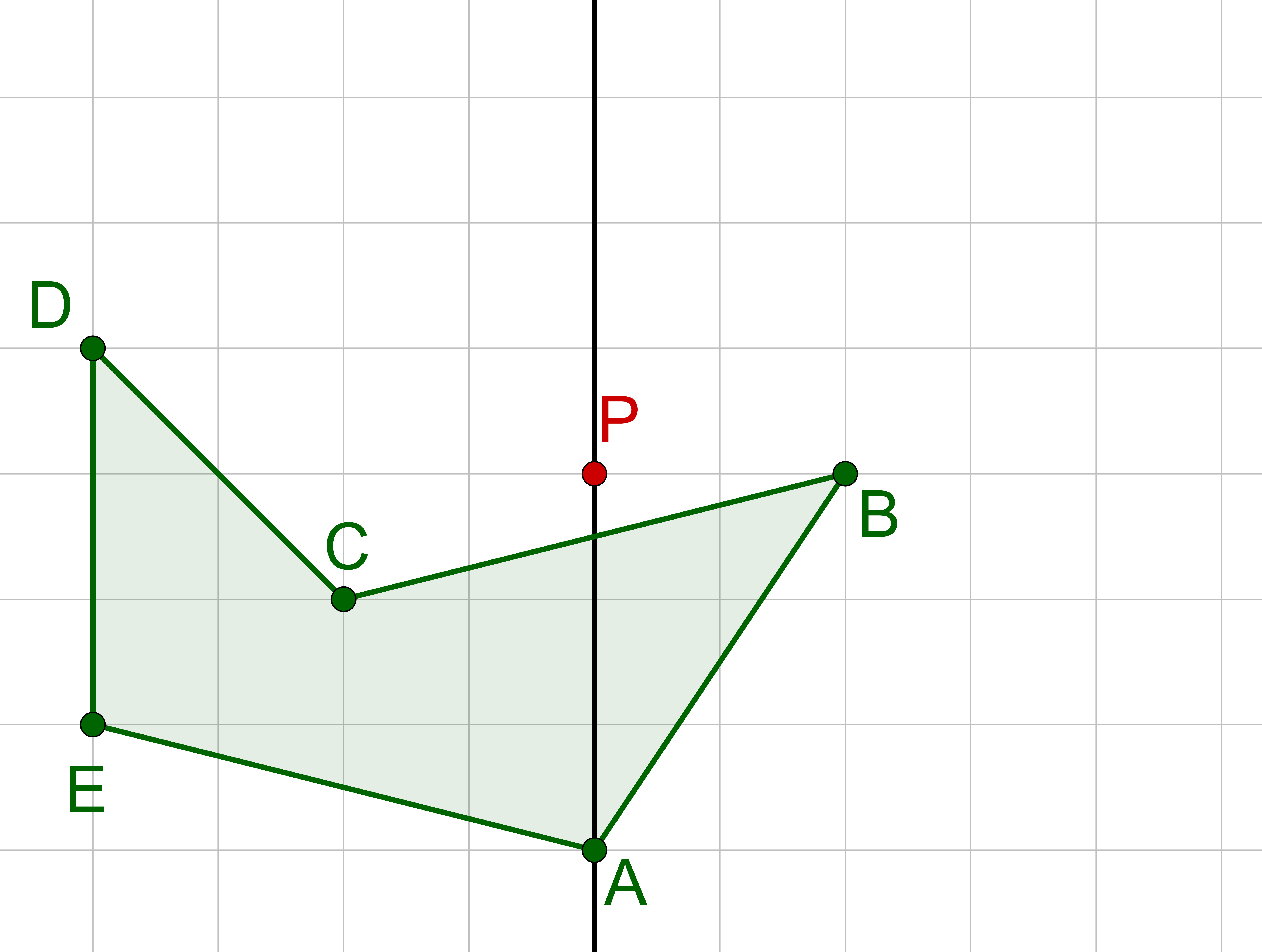
  Wähle Punkt $B$ und spiegle den Punkt $B$ an $P$ .
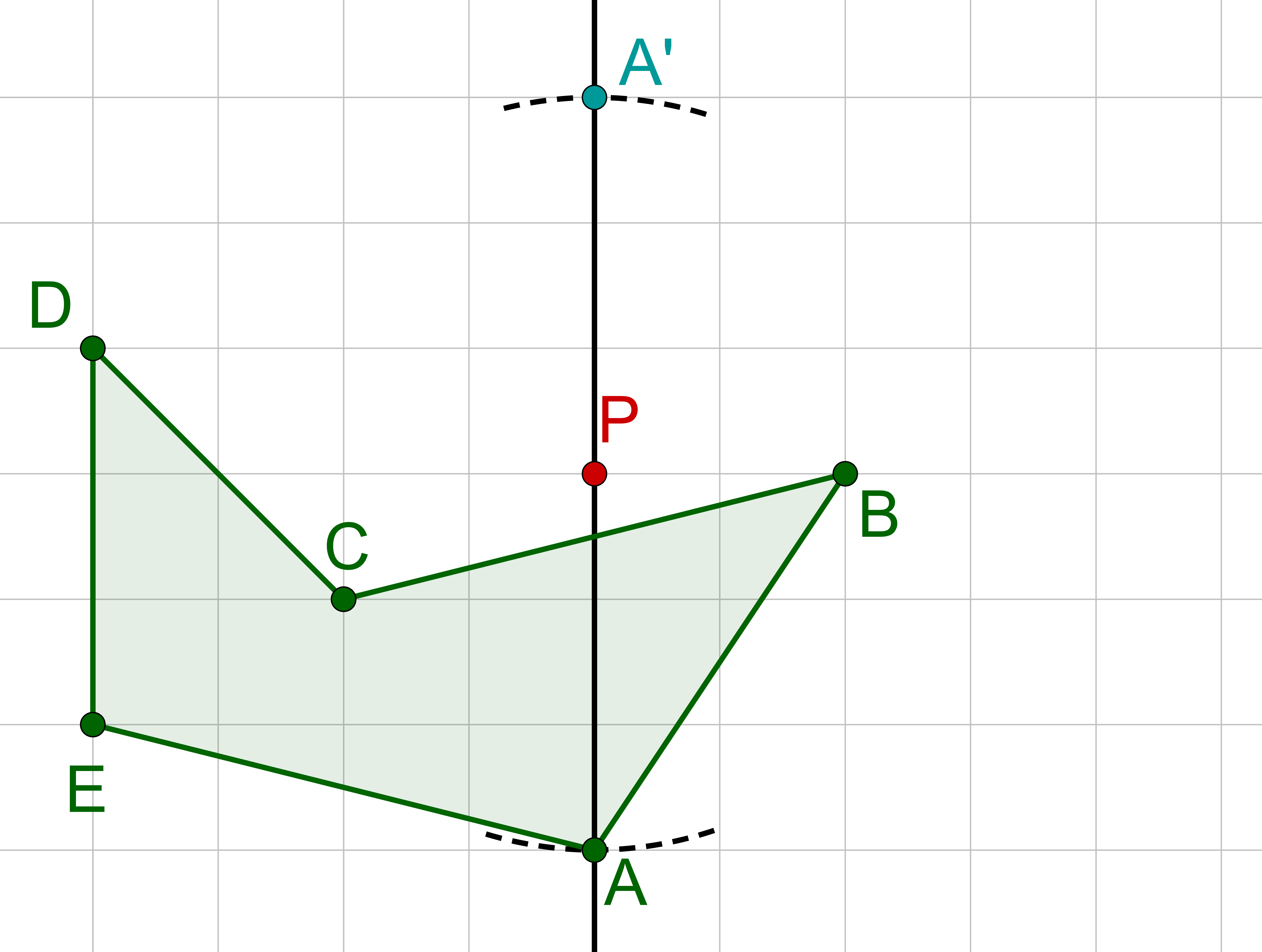
  Wiederhole dies für die restlichen Punkte.
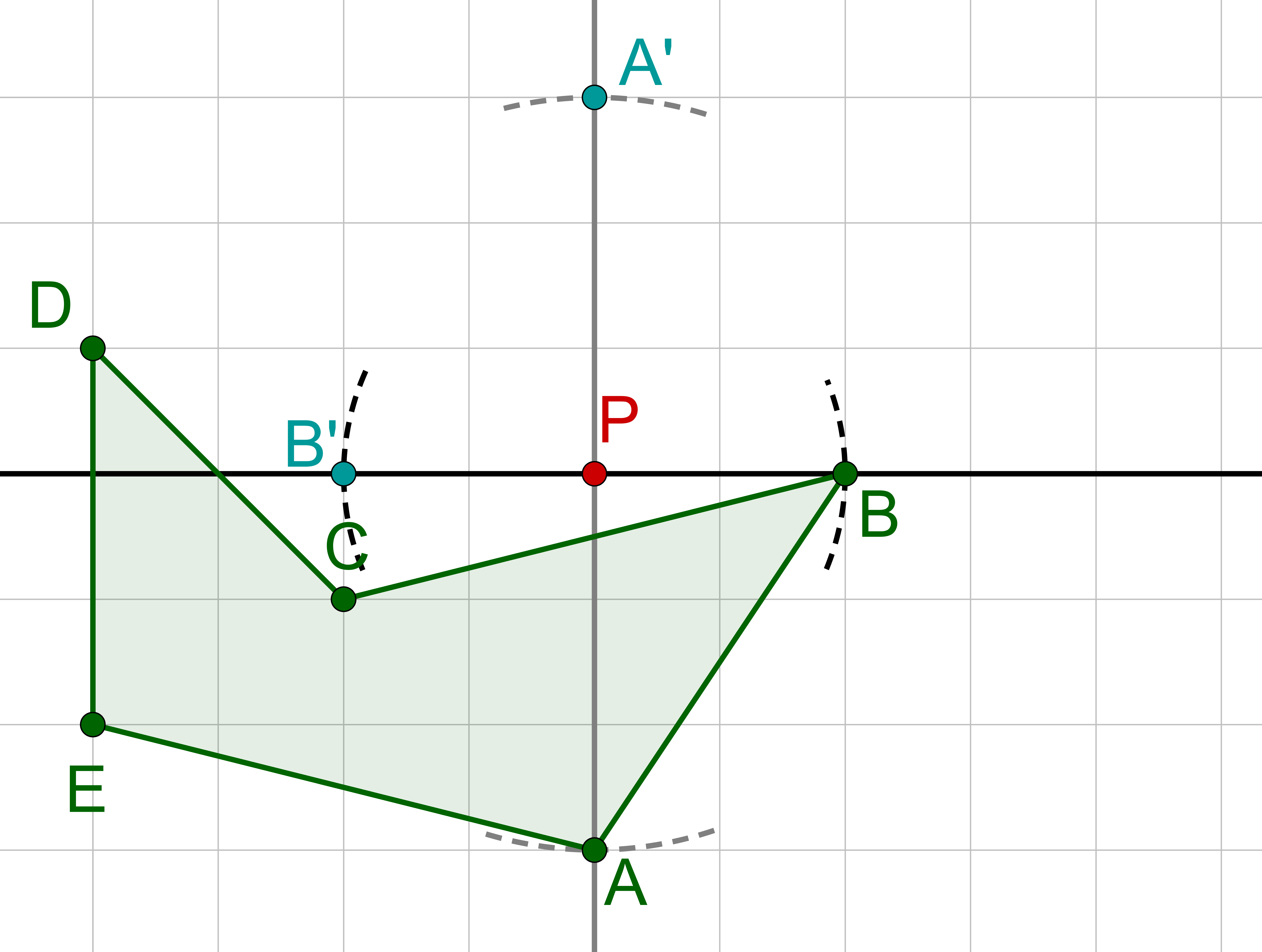
  Verbinde die gespiegelten Punkte in der richtigen Reihenfolge.
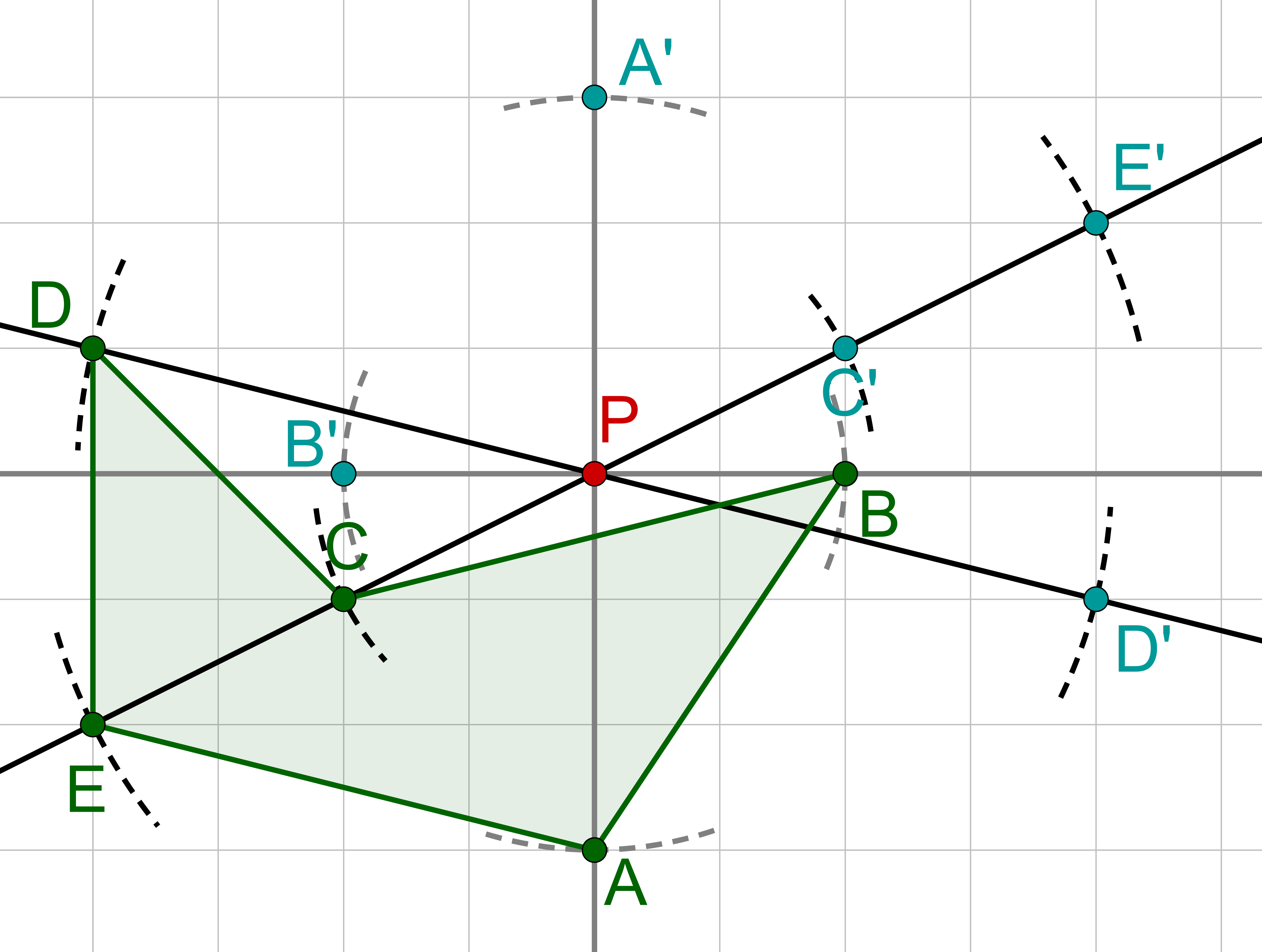
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
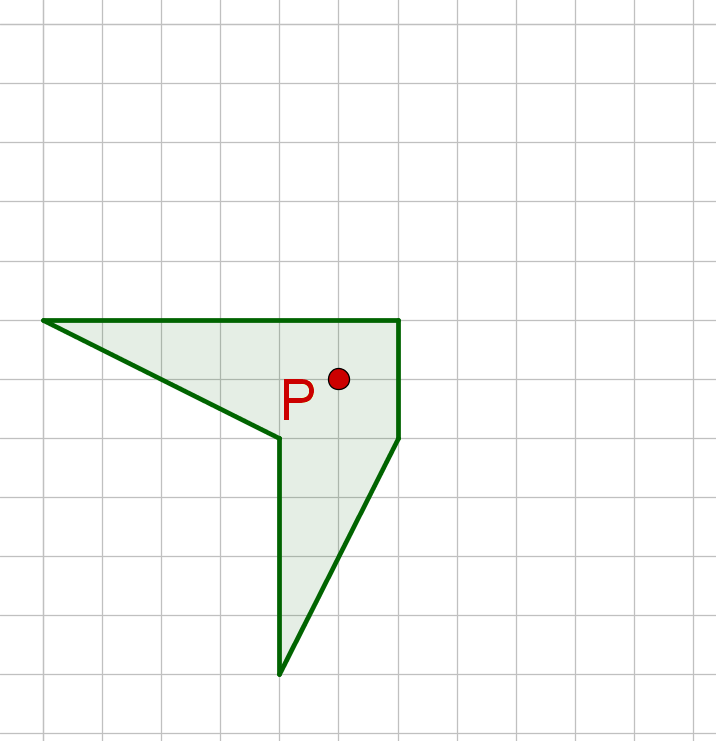
3. Für diese Aufgabe benötigst Du folgendes Grundwissen: Punktspiegelung
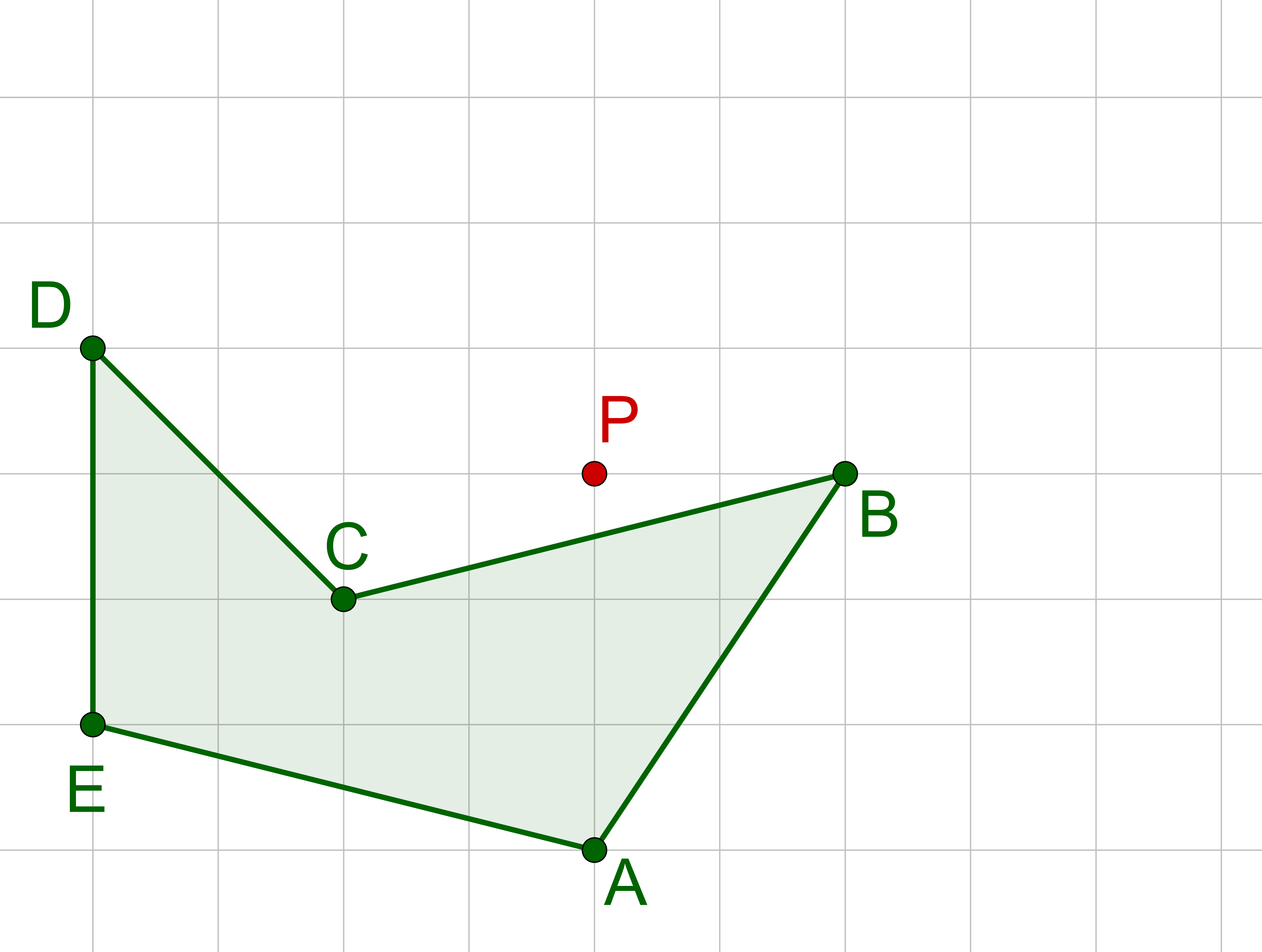
  Bestimme die charakteristischen Punkte der Figur.
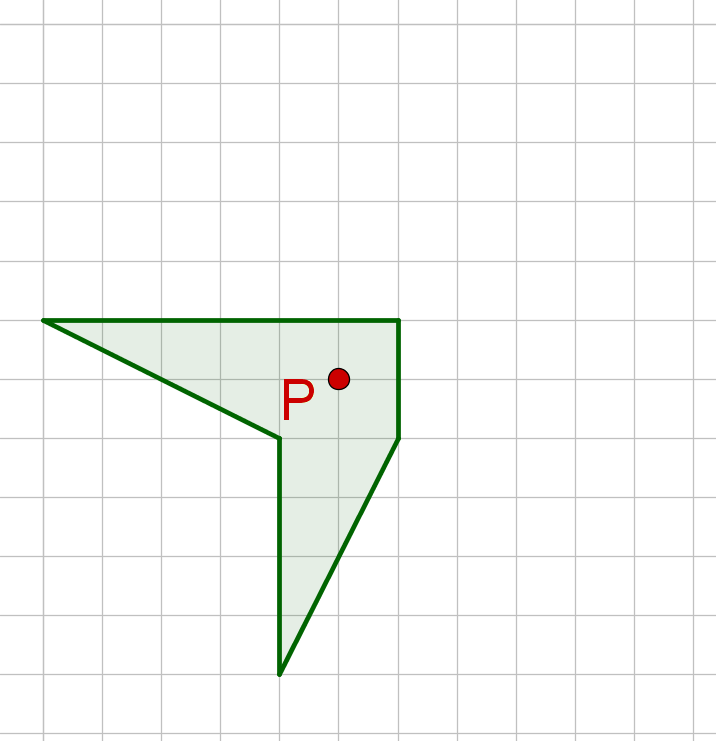
  Wähle Punkt $A$ und spiegele ihn an $P$ .
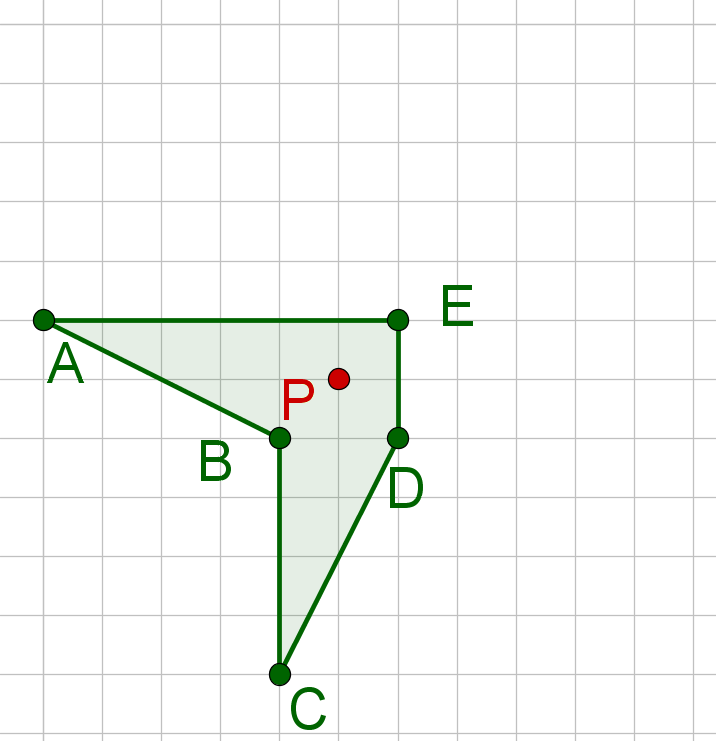
  Wiederhole dies für alle charakteristischen Punkte.
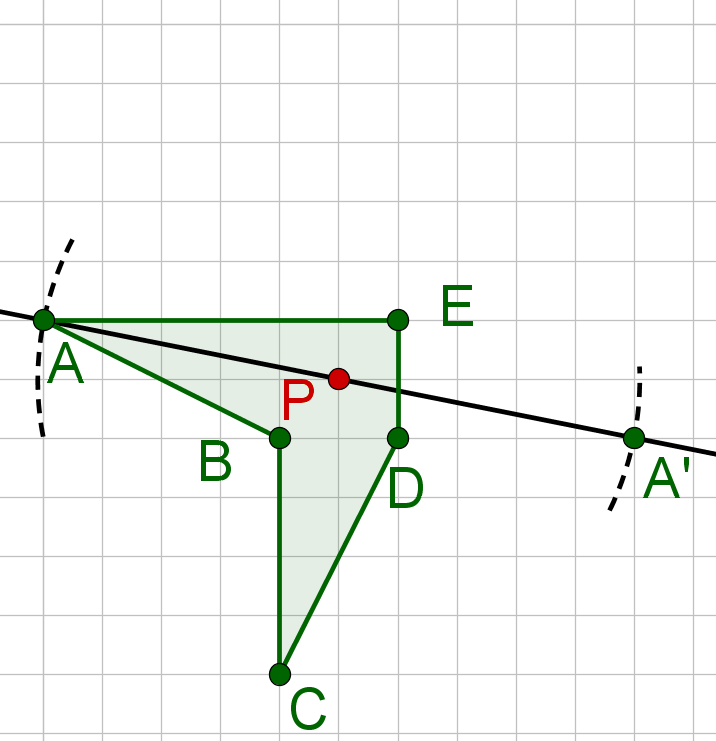
  Verbinde die Punkte in der richtigen Reihenfolge.
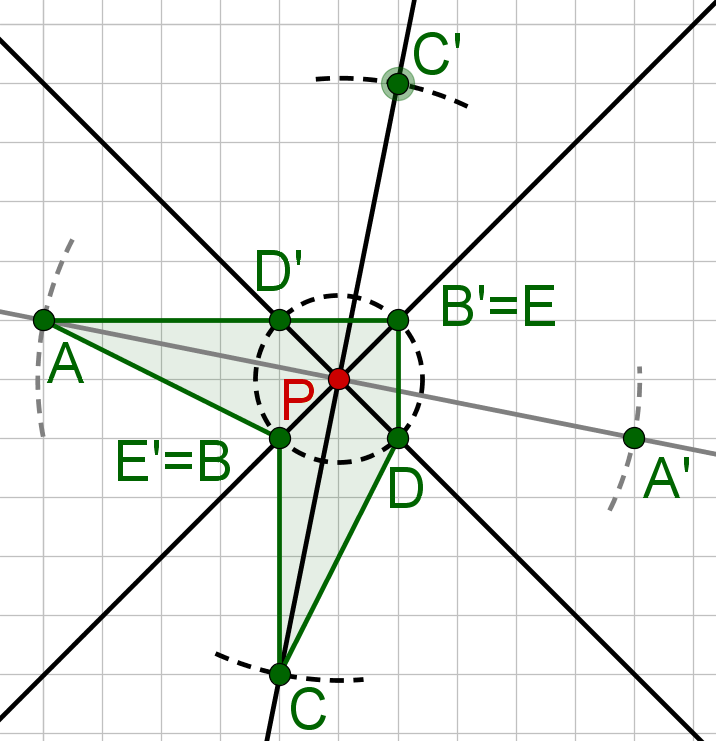
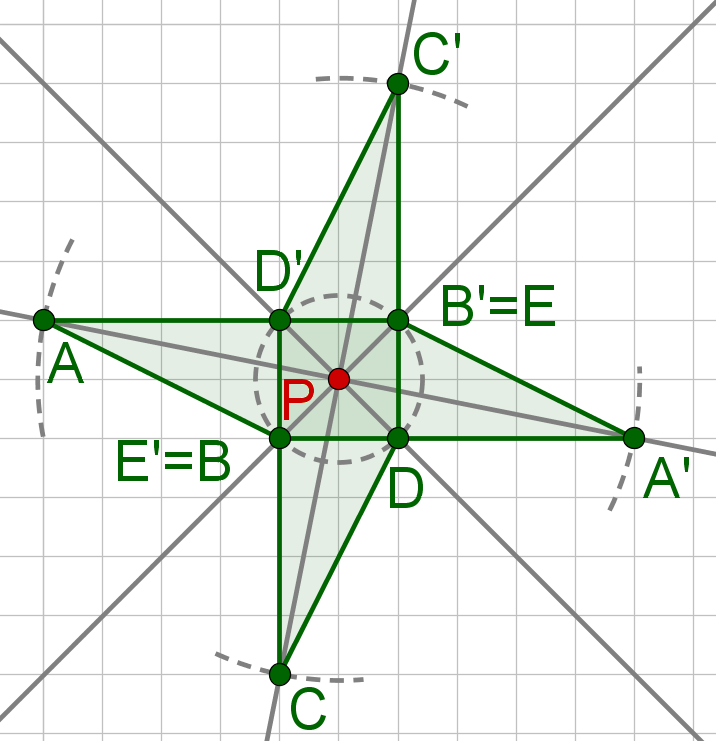
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Zeichne die Figur in ein Koordinatensystem. Spiegle sie dann am Zentrum $P$ .
1. Punkte: $A(1|0)$ , $B(2|3)$ , $C(3|-1)$ , $D(-1|-1)$
  Zentrum: $P(0|0)$
  Strecken: $[AB]$ , $[BC]$ , $[CD]$ , $[DA]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punktspiegelung
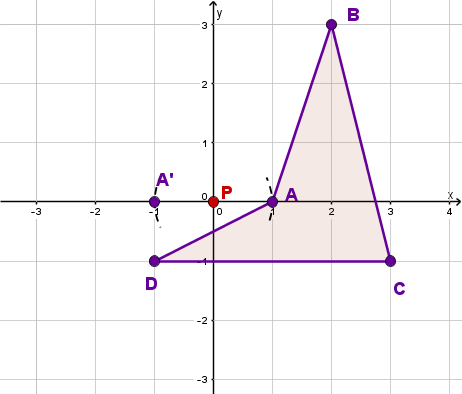
  Spiegle Punkt $A$ an $P$ . Hierbei muss keine Verbindungsgerade mehr gezeichnet werden, da $P$ und $A$ bereits beide auf der x-Achse liegen. Es reicht also einen Kreis mit Radius $[PA]=1$ um P zu zeichnen um den Spiegelpunkt $A'$ als Schnittpunkt des Hilfskreises mit der x-Achse zu finden.
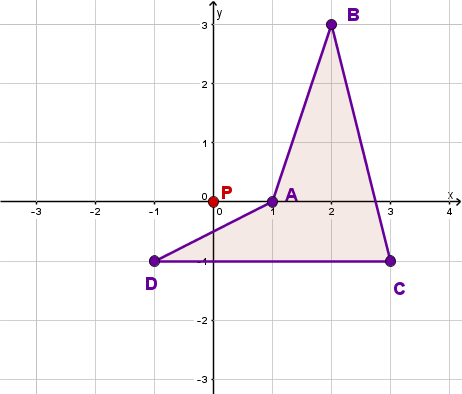
  Spiegle nun $B$ an $P$ um $B'$ zu erhalten, indem du die Gerade $BP$ mit dem Kreis um $P$ mit Radius $[BP]$ schneidest.
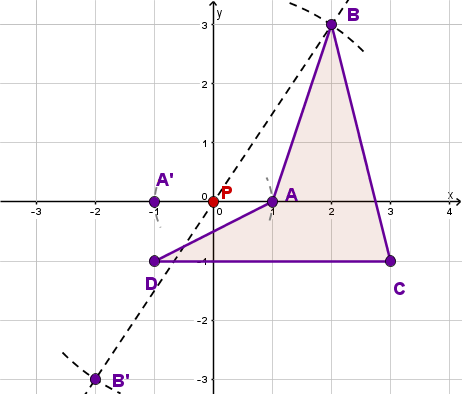
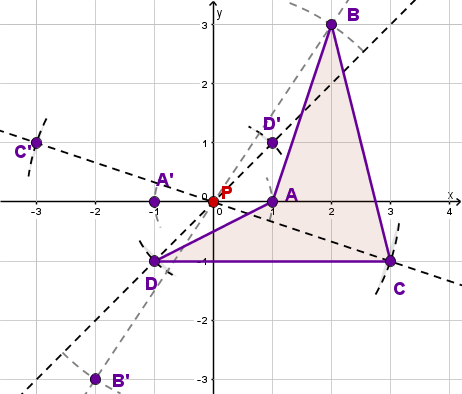
  Wiederhole dies für die restlichen beiden Punkte $C$ und $D$ um deren Spiegelpunkte $C'$ und $D'$ zu finden.
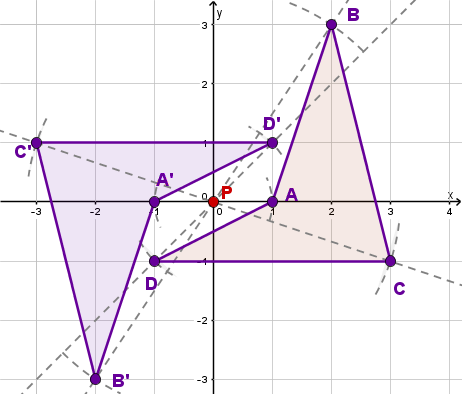
  Verbinde die Punkte $A'$ , $B'$ , $C'$ und $D'$ in der richtigen Reihenfolge.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Kreis um $A(3|3)$ , wenn $B(6|3)$ auf dem Kreis liegt.
  Zentrum: $P(3|2)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punktspiegelung
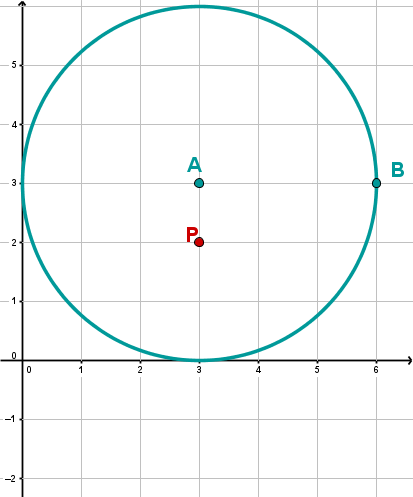
  Zeichne zuerst die Punkte ein. Miss dann mit dem Zirkel den Abstand zwischen $A$ und $B$ und male einen Kreis um $A$ mit dieser Länge.
  Um den Punkt $A$ an $P$ zu spiegeln zeichne eine Gerade durch $A$ und $P$ und ziehe dann mit dem Zirkel einen Kreis mit dem Radius $[AP]$ um $P$ . Der Schnittpunkt der Geraden mit dem Kreis ist der Spiegelpunkt $A'$ .
  Ziehe nun einen Kreis mit dem Radius $[AB]$ um $A'$ . Den Radius kannst du einfach von oben übertragen mit dem Zirkel.
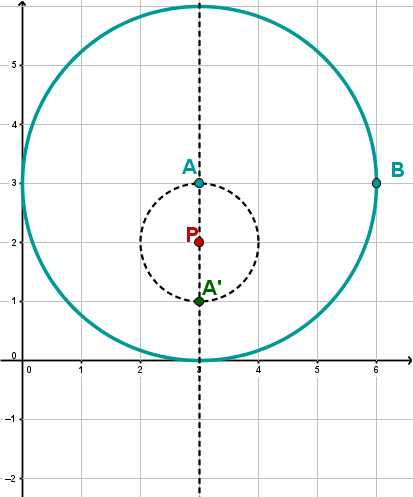
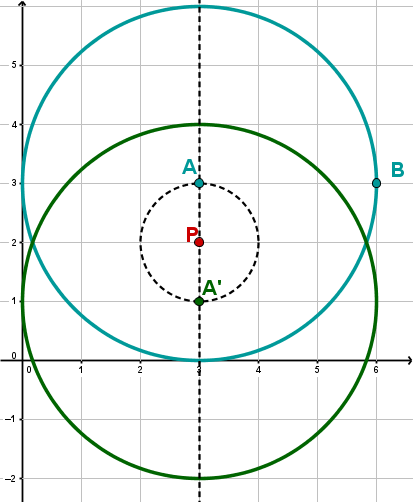
  Alternative: Man kann auch Punkt $B$ an $P$ spiegeln und dann den Kreis um $A'$ durch den Spiegelpunkt $B'$ ziehen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.