Teil A - lernen mit Serlo!

Dieser Inhalt wurde gelöscht.

3.0 Gegeben sind Drachenvierecke $A B_{n} C D_{n}$ mit der Symmetrieachse $A C$ . Punkte $E_{n}$ sind die Mittelpunkte der Strecken $[B_{n} D_{n}]$ . Die Winkel $B_{n} C E_{n}$ haben das Maß $φ$ mit $\begin{array}{l} φ \in] 0^{\circ}; 90^{\circ} [. \end{array}$

Es gilt: $A C = 2 cm$ und $B_{n} C = C D_{n} = 3 cm .$

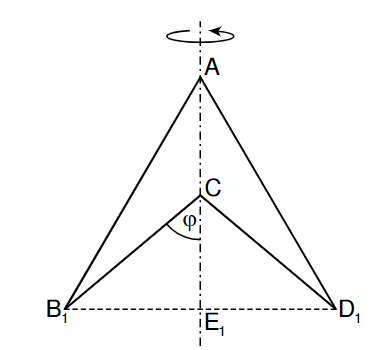
Die nebenstehende Zeichnung zeigt das Drachenviereck $A B_{1} C D_{1}$ für $φ = 50^{\circ}$ .

3.1 Zeigen Sie durch Rechnung, dass für die Längen der Strecken $[B_{n} E_{n}]$ und $[A E_{n}]$ in Abhängigkeit von $φ$ gilt:

$B_{n} E_{n} (φ) = 3 \cdot sin φ cm$ und $A E_{n} (φ) = (3 \cdot cos φ + 2) cm .$

3.2 Die Drachenvierecke $A B_{n} C D_{n}$ rotieren um die Gerade $A C$ .

Bestätigen Sie rechnerisch, dass für das Volumen $V$ der entstehenden Rotationskörper in Abhängigkeit von $φ$ gilt: $V (φ) = 6 \cdot π \cdot {sin}^{2} φ {cm}^{3}$ .

3.3 Eine der folgenden Aussagen zu den Rotationskörpern aus 3.2 ist richtig. Kreuzen Sie diese Aussage an.

Es gibt einen Rotationskörper mit einem Volumen von $6 \cdot π$ ${cm}^{3}$ .
Die Rotationskörper haben ein Volumen von höchstens $6$ ${cm}^{3}$ .
Für das Volumen $V$ gilt: $V (φ) < 6 \cdot π$ ${cm}^{3}$ .
Für das Volumen $V$ gilt: $V (φ) > 6 \cdot π$ ${cm}^{3}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrische Funktion

Teilaufgabe 3.1

Die Längen der Strecken [ $B_{n} E_{n}$ ] und $[A E_{n}]$ :

$[B_{n} E_{n}]$ im rechtwinkligen Dreieck $B_{n} E_{n} C$ mithilfe der Trigonometrie:

$\sin (φ)$	$=$	$\frac{Gegenkathete}{Hypotenuse}$
$\sin (φ)$	$=$	$\frac{B_{n} E_{n}}{B_{n} C}$
$\sin (φ)$	$=$	$\frac{B_{n} E_{n}}{3 cm}$	$\cdot 3 cm$
$B_{n} E_{n}$	$=$	$\sin (φ) \cdot 3 cm$
$B_{n} E_{n}$	$=$	$3 \cdot \sin φ cm$

$[A E_{n}] = [C E_{n}] + 2 cm$ .

$[C E_{n}]$ im rechtwinkligen Dreieck $B_{n} E_{n} C$ mithilfe der Trigonometrie:

$\cos φ$	$=$	$\frac{Ankathete}{Hypotenuse}$
$\cos φ$	$=$	$\frac{C E_{n}}{B_{n} C}$
$\cos φ$	$=$	$\frac{C E_{n}}{3 cm}$	$\cdot 3 cm$
$C E_{n}$	$=$	$\cos φ \cdot 3 cm$
$C E_{n}$	$=$	$(3 \cdot \cos φ) cm$

$[A E_{n}] = [C E_{n}] + 2 cm = (3 \cdot \cos φ) cm + 2 cm = (3 \cdot \cos φ + 2) cm$

Teilaufgabe 3.2

Das Volumen $V_{R}$ des Rotationskörpers $A B_{n} C D_{n}$ in Abhängigkeit von $φ$ :

$V_{Rotationskörpers} = V_{Kegel A B_{n} D_{n}} - V_{Kegel C B_{n} D_{n}}$

$V_{Kegel A B_{n} D_{n}}$	$=$	$\frac{1}{3} \cdot r^{2} \cdot π \cdot h$
	$=$	$\frac{1}{3} \cdot {B_{n} E_{n}}^{2} \cdot π \cdot A E_{n}$

$V_{Kegel C B_{n} D_{n}}$	$=$	$\frac{1}{3} \cdot r^{2} \cdot π \cdot h$
	$=$	$\frac{1}{3} \cdot {B_{n} E_{n}}^{2} \cdot π \cdot C E_{n}$

$V_{R}$	$=$	$V_{Kegel A B_{n} D_{n}} - V_{Kegel C B_{n} D_{n}}$
	$=$	$\frac{1}{3} \cdot {B_{n} E_{n}}^{2} \cdot π \cdot A E_{n} - \frac{1}{3} \cdot {B_{n} E_{n}}^{2} \cdot π \cdot C E_{n}$
	$=$	$\frac{1}{3} \cdot π \cdot {B_{n} E_{n}}^{2} (A E_{n} - C E_{n})$
	$=$	$[\frac{1}{3} \cdot π \cdot 3^{2} \cdot \sin^{2} φ (3 \cdot \cos φ + 2 - 3 \cdot \cos φ)] {cm}^{3}$
	$=$	$[\frac{1}{3} \cdot π \cdot 3^{2} \cdot \sin^{2} φ \cdot 2] {cm}^{3}$
	$=$	$6 \cdot π \cdot \sin^{2} φ {cm}^{3}$

Teilaufgabe 3.3

Richtige Aussagen zu den Rotationskörpern aus A 3.2:

Es gibt einen Rotationskörper mit einem Volumen von $6 \cdot π {cm}^{3}$ .

Wenn $V_{R} = 6 \cdot π {cm}^{3}$ ist, kann ich $φ$ berechnen, indem ich nach $φ$ auflöse:

$V_{R}$	$=$	$6 \cdot π {cm}^{3}$
$6 \cdot π \cdot \sin^{2} φ {cm}^{3}$	$=$	$6 \cdot π {cm}^{3}$	$: (6 \cdot π {cm}^{3})$
$\sin^{2} φ$	$=$	$1$	$\sqrt{}$
$\sin φ$	$=$	$\sqrt{1}$	$\sin^{- 1}$
$φ$	$=$	$90^{\circ}$

Laut der Angabe aus 3.0 darf der Winkel nicht gleich $90^{\circ}$ werden: $φ \in] 0^{\circ}; 90^{\circ} [$

Folglich ist die erste Aussage falsch.

Die Rotationskörper haben ein Volumen von höchstens $6 {cm}^{3}$ .

Wenn $φ$ sehr klein ist, ist auch $\sin (φ)$ sehr klein, und dann ist auch $π \cdot \sin^{2} (φ) < 1$ . Damit ist $V (φ) = 6 π \sin^{2} (φ) {cm}^{3} < 6 {cm}^{3}$ . Also ist auch Aussage 2 falsch.

Für das Volumen V gilt: $V (φ) < 6 \cdot π {cm}^{3}$ .

Diese Aussage ist richtig, da für $0 < φ < 90^{\circ}$ immer $0 < \sin^{2} (φ) < 1$ ist.

Zum Beispiel für $φ = 50^{\circ}$

$V (50^{\circ}) = 6 \cdot π \cdot \sin^{2} (50^{\circ}) {cm}^{3} \approx 11,06 {cm}^{3} < 6 \cdot π {cm}^{3}$

Für das Volumen V gilt: $V (φ) > 6 \cdot π {cm}^{3}$ .

Diese Aussage ist wegen $\sin^{2} (φ) < 1$ falsch.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?