Analysis, Teil B, Aufgabengruppe 1

Nun wird die in $ℝ$ definierte Integralfunktion $F : x \mapsto \int_{0}^{x} f (t) d t$ betrachtet; ihr Graph wird mit $G_{F}$ bezeichnet.

a) Begründen Sie, dass $F$ in $x = 0$ eine Nullstelle hat, und machen Sie mithilfe des Verlaufs von $G_{f}$ plausibel, dass im Intervall $[1; 3]$ eine weitere Nullstelle von $F$ liegt. Geben Sie an, welche besondere Eigenschaft $G_{F}$ im Punkt $(- 1 | F (- 1))$ hat, und begründen Sie Ihre Angabe.

b) Die Gerade mit der Gleichung $y = x - 1$ begrenzt gemeinsam mit den Koordinatenachsen ein Dreieck. Geben Sie den Flächeninhalt dieses Dreiecks und den sich daraus ergebenden Näherungswert für $F (1)$ an.

c) Die Abbildung 2 zeigt den Graphen $G_{f}$ sowie den Graphen $G_{g}$ der in $ℝ$ definierten Funktion

$g : x \mapsto - \cos (\frac{π}{2} x)$ .

Beschreiben Sie, wie $G_{g}$ aus dem Graphen der in $ℝ$ definierten Funktion $x \mapsto \cos x$ hervorgeht, und berechnen Sie durch Integration von $g$ einen weiteren Näherungswert für $F (1)$ .

(zur Kontrolle: $F (1) \approx - \frac{2}{π}$ )

d) Berechnen Sie das arithmetische Mittel der beiden in den Aufgaben 2b und 2c berechneten Näherungswerte. Skizzieren Sie den Graphen von $F$ für $0 \leq x \leq 3$ unter Berücksichtigung der bisherigen Ergebnisse in der Abbildung 1.

Teilaufgabe a)

$F : x \to F (x) = \int_{o}^{x} f (t) d t$

hat an der Stelle $x_{0}$ =0 eine Nullstelle, da untere und obere Grenze des Integrals gleich sind.

Im Intervall $[1; 3]$ liegt eine weitere Nullstelle, wenn man einen Vorzeichenwechsel von $F$ in diesem Intervall nachweisen kann.

$F (1) = \int_{0}^{1} f (t) d t < 0$ ,

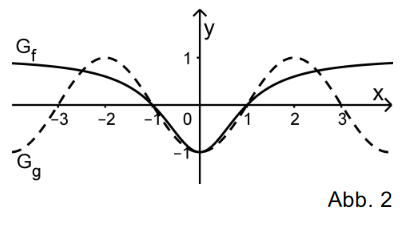
Im Intervall $[0; 1 [$ liegt der Graph $G_{f}$ unterhalb der $x$ -Achse. Somit ist der Integrand $f (t)$ in diesem Intervall negativ. Damit gilt auch $F (1) < 0$ .

Da der Graph $G_{f}$ in diesem Intervall gut durch eine Gerade mit dem $x$ -Achsen Abschnitt $x_{0} = 1$ und dem $y$ -Achsenabschnitt $y_{0} = - 1$ angenähert wird, kann man den Wert von $F (1)$ mit $- \frac{1}{2}$ abschätzen.

$F (3) = \int_{0}^{3} f (t) d t = \int_{0}^{1} f (t) d t + \int_{1}^{3} f (t) d t$

Auf Grund der vorgegebenen Skizze des Graphen $G_{f}$ kann man

$\int_{1}^{3} f (t) d t$ mit etwa $\frac{3}{4}$ abschätzen.

Damit ergibt sich für $F (3) = - \frac{1}{2} + \frac{3}{4} > 0$ .

Also hat $F$ neben $x_{0} = 0$ im Intervall $[1; 3]$ eine weitere Nullstelle.

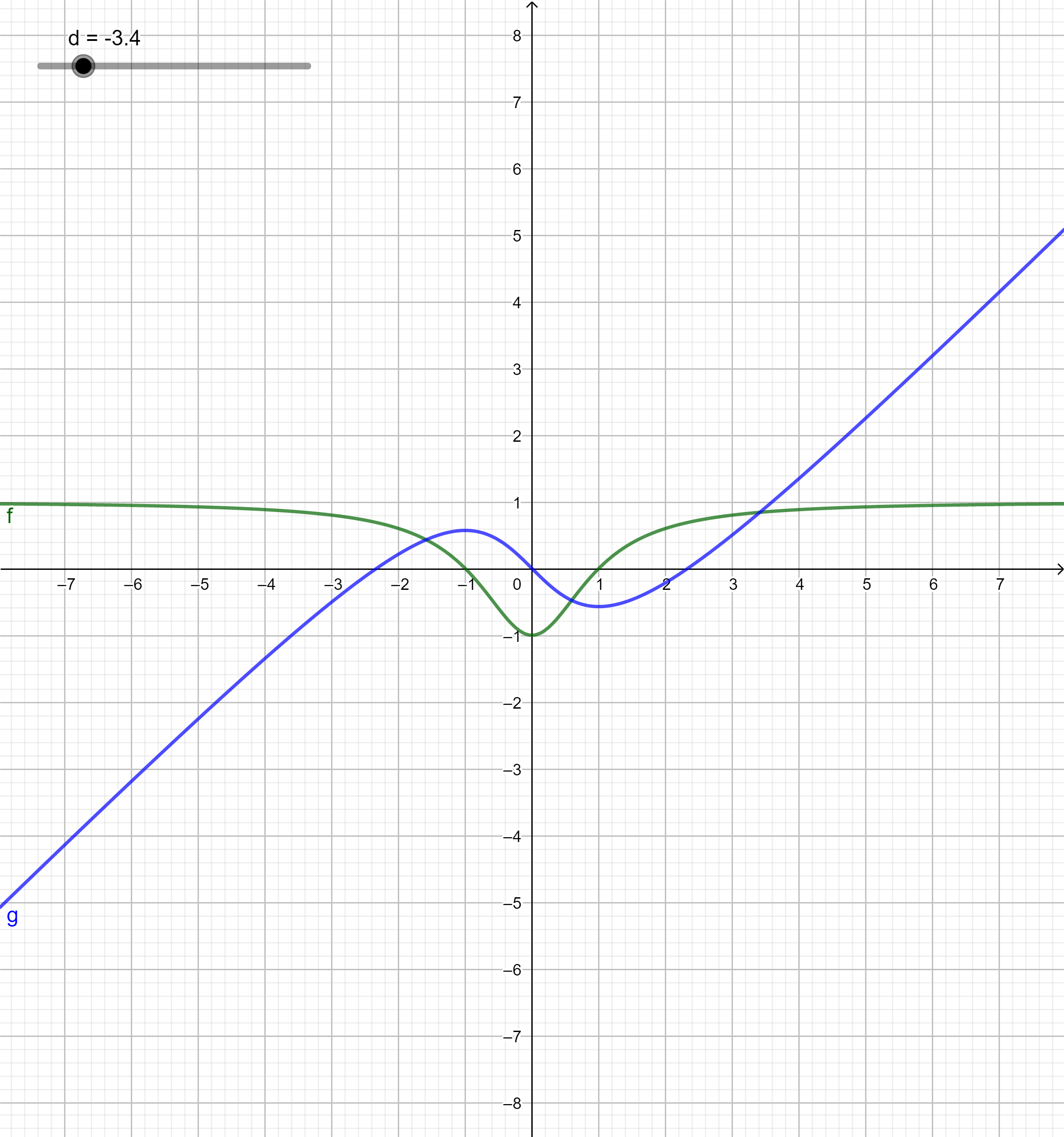
Im Punkt $P (- 1 | F (- 1))$ liegt ein Maximum (Hochpunkt) des Graphen $G_{F}$ .

Begründung: Der Graph $G_{f}$ stellt die 1. Ableitung von $F$ da.

Aus dem Graph $G_{f}$ liest man ab:

Für $x < - 1$ gilt: $f (x) > 0 \Rightarrow F$ wachsend.

für $- 1 < x < 1$ gilt: $f (x) < 0 \Rightarrow F$ fallend.

Teilaufgabe b)

Die Gerade $y = x - 1$ begrenzt mit den Koordinatenachsen ein Dreieck.

Dieses Dreieck ist rechtwinklig mit den Kathetenlängen $a = b = 1 \Rightarrow$

$A_{Δ} = \frac{1}{2} \cdot 1 \cdot 1 = \frac{1}{2} \Rightarrow F (1) = \frac{1}{2} F E$

Teilaufgabe c)

$g (x) = - \cos (\frac{π}{2} x)$

Im Vergleich zur Grundfunktion $a (x) = \cos (x)$ ist die Periode von $g$ verändert.

Für die Periode von $g$ gilt: $p = \frac{2 π}{\frac{π}{2}} = \frac{2 π \cdot 2}{π} = 4$ .

Falls man diese Regel nicht parat hat, so hat man zwei Möglichkeiten:

Aus dem Graphen $G_{g}$ kann man ablesen, dass $x_{0} = - 1$ und $x_{1} = 1$ benachbarte Nullstellen sind. Also wäre $\frac{p}{2} = 2 \Rightarrow p = 4$
Oder man erinnert sich, dass $f (x) = \sin (2 \cdot x)$ die Periode $p = π$ hat. Und allgemein gilt: $f (x) = \sin (a \cdot x)$ hat die Periode $p = \frac{2 π}{a}$

Zusätzlich zur Periodenänderung wird der Graph noch an der $x$ -Achse gespiegelt.

Näherungswert für $F (1)$ :

$F (1) = \int_{0}^{1} [- \cos (\frac{π}{2} \cdot x) d x = - \frac{2}{π} \int_{0}^{1} \cos (\frac{π}{2} \cdot x) \cdot \frac{π}{2} d x ⟺$

$F (1) = - \frac{2}{π} \cdot \sin (\frac{π}{2} \cdot x) |_{0}^{1} = - \frac{2}{π} \cdot [\sin (\frac{π}{2}) - \sin (0)] = - \frac{2}{π} \cdot [1 - 0] = - \frac{2}{π}$

Teilaufgabe d)

arithmetisches Mittel aus den beiden Näherungswerten:

$m = \frac{\frac{- 1}{2} + \frac{- 2}{π}}{2} \approx - \frac{1,137}{2} \approx - 0,57$

Die Funktion von $F$ hat an der Stelle $x = - 1$ eine Maximumstelle.

Da die Funktion f, wie in a) gezeigt, achsensymmetrisch ist, ist $F$ als Integralfunktion zu $f$ punktsymmetrisch, weil, wie in 2a) gezeigt, $F (0) = 0$ gilt.

Somit hat $F$ an der Stelle $x = 1$ eine Minimumstelle.

Es gilt nämlich:

Ist $f$ achsensymmetrisch, so ist $F$ punktsymmetrisch, falls $F (0) = 0$ ist.

Achsensymmetrie: $f (x) = f (- x)$ für alle $x$ (*)

Punktsymmetrie: $F (x) = - F (- x)$ für alle $x$

Wir definieren $F (x) = \int_{0}^{x} f (t) d t$ und verwenden die Substitutionsregel:

$t = g (u) = - u$ . Dann ist $u = - t$ und es gilt:

$t = 0 ⟺ u = 0$ und $t = x ⟺ u = - x$ .

Außerdem ist $g^{'} (u) = - 1.$

$F (x) = \int_{0}^{x} f (t) d t = \int_{0}^{- x} f (u) (- 1) d u = - \int_{0}^{- x} f (u) d u = - F (- x)$

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?