Analysis, Teil B, Aufgabengruppe 2

Gegeben ist die Funktion $f: x \mapsto 1+7e^{-0{,}2x}$ mit Definitionsbereich $\R^+_0$ ; die Abbildung 1 zeigt ihren Graphen $G_f$ .

a) Begründen Sie, dass die Gerade mit der Gleichung $y = 1$ waagrechte Asymptote von $G_f$ ist. Zeigen Sie rechnerisch, dass $f$ streng monoton abnehmend ist.

Für jeden Wert $s>0$ legen die Punkte $(0|1)$ , $(s|1)$ , $(s| f (s) )$ und $(0|f (s) )$ ein Rechteck mit dem Flächeninhalt $R(s)$ fest.

b) Zeichnen Sie dieses Rechteck für $s = 5$ in die Abbildung 1 ein. Zeigen Sie, dass $R(s)$ für einen bestimmten Wert von $s$ maximal ist, und geben Sie den Wert von $s$ an.

(zur Kontrolle: $R(s) = 7s \cdot e^{-0{,}2s}$ )

c) Berechnen Sie den Inhalt des Flächenstücks, das von $G_f$ , der y-Achse sowie den Geraden mit den Gleichungen $y = 1$ und $x=5$ begrenzt wird. Einen Teil dieses Flächenstücks nimmt das zu $s = 5$ gehörige Rechteck ein. Bestimmen Sie den prozentualen Anteil des Flächeninhalts dieses Rechtecks am Inhalt des Flächenstücks.

Teilaufgabe a)

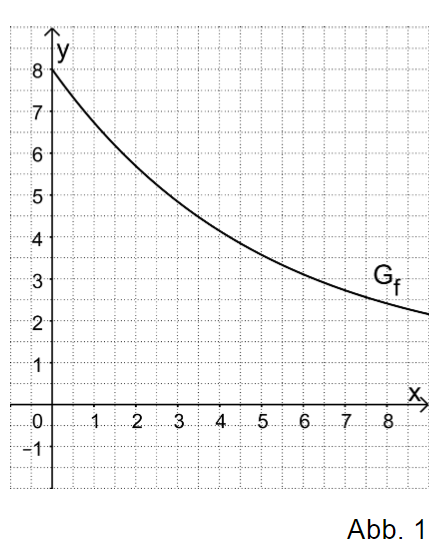
Die e-Funktion $e_1(x)=e^x$ hat die x-Achse als waagrechte Asymptote. Da $e_2(x)=e^{-x}$ sich aus $e_1(x)$ durch Spiegelung an der y-Achse ergibt, ist die x-Achse ebenfalls eine waagrechte Asymptote von $e_2(x)$ .

Der Graph $G_{e_2}$ ergibt sich aus dem Graph $G_{e_1}$ durch Spiegelung an der y-Achse.

Also gilt: $\lim\limits_{x\to\infty}e^{-x}$ =0 und $\lim\limits_{x\to\infty}(1+7\cdot e^{-{0{,}2\cdot x}})=1$

Die Funktion $f$ ist streng monoton fallend, wenn $f'(x)<0$ für alle $x>0$

\displaystyle f'(x)=7\cdot(-0{,}2)\cdot e^{-0{,}2\cdot x}=-1{,}4\cdot e^{-0{,}2\cdot x}<0

Da $e^{-0{,}2\cdot x}>0$ , ist also $-1{,}4\cdot e^{-0{,}2\cdot x}<0$ . Somit ist $f$ streng monoton fallend.

Teilaufgabe b)

Bei dieser Aufgabe gehst du in zwei Schritten vor:

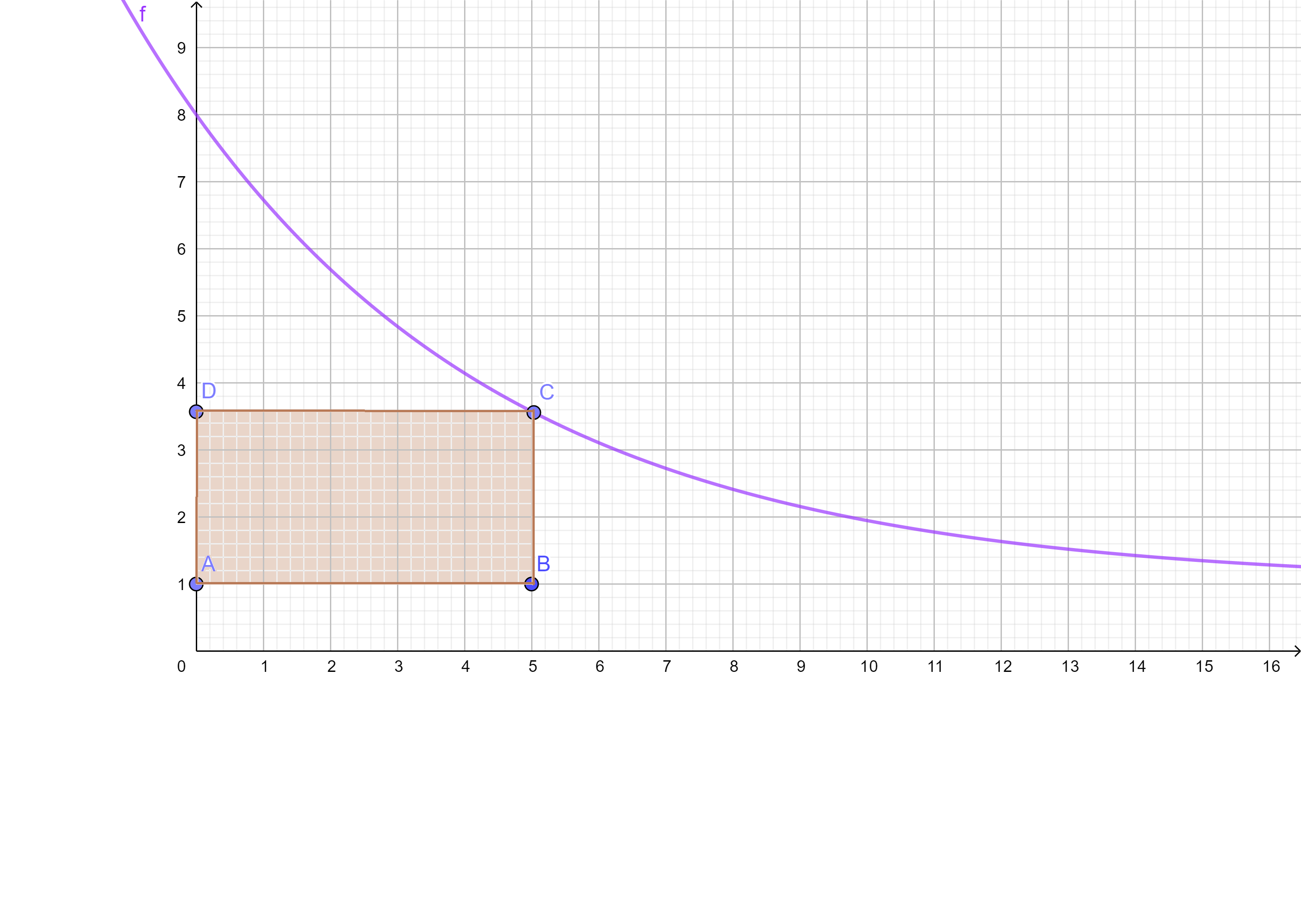
Zuerst berechnest du die Fläche des Rechtecks R(s) in Abhängigkeit von $s$ .
Dann berechnest du mithilfe der ersten Ableitung, wann R(s) maximal wird.

Das Rechteck mit den gegebenen Punkten hat die Länge $s$ und die Höhe

\displaystyle f'(x)=7\cdot(-0{,}2)\cdot e^{-0{,}2\cdot x}=-1{,}4\cdot e^{-0{,}2\cdot x}<0

Damit gilt für den Flächeninhalt:

\displaystyle f'(x)=7\cdot(-0{,}2)\cdot e^{-0{,}2\cdot x}=-1{,}4\cdot e^{-0{,}2\cdot x}<0

Dieser Wert wird maximal für den Wert von $s$ , wenn $R'(s)=0$ und an der Stelle $s$ einen Vorzeichenwechsel von $+$ nach $-$ hat.

\displaystyle f'(x)=7\cdot(-0{,}2)\cdot e^{-0{,}2\cdot x}=-1{,}4\cdot e^{-0{,}2\cdot x}<0

Berechne nun die Nullstelle von R(s):

$\displaystyle R'\left(s\right)$	$=$	$\displaystyle 0$
	↓	Setze R'(s) ein
$\displaystyle 1-0{,}2\ \cdot s$	$=$	$\displaystyle 0$	$\displaystyle -1$
$\displaystyle -0{,}2\cdot s$	$=$	$\displaystyle -1$	$\displaystyle \cdot\left(-5\right)$
$\displaystyle s$	$=$	$\displaystyle 5$

Da der Faktor $7\cdot e^{-0{,}2\cdot s}$ immer größer als 0 ist, wird das Vorzeichen von $R'(s)$ bestimmt von dem zweiten Faktor $1-\frac{1}{5}\cdot s$

Der zweite Faktor ist eine fallende Gerade mit dem y-Achsenabschnitt 1 und der Nullstelle $s=5$ .

Also ist $R'(s)>0$ für $0<s<5$ : $R$ wachsend.

Und $R'(s)<0$ für $5<s<\infty$ : $R$ fallend.

Damit wird der Inhalt des Rechteckes für $s=5$ maximal. Es gilt:

\displaystyle f'(x)=7\cdot(-0{,}2)\cdot e^{-0{,}2\cdot x}=-1{,}4\cdot e^{-0{,}2\cdot x}<0

Teilaufgabe c)

Für den Inhalt des vor beschriebenen Flächenstücks gilt:

$\displaystyle A$	$=$	$\displaystyle \int_0^5(f(x)-1)\,dx$	$\displaystyle$
	↓	Setze f(x) ein
	$=$	$\displaystyle \int_0^5(1+7\cdot e^{-0{,}2x}-1)\,dx$
	↓	Vereinfache
	$=$	$\displaystyle \int_0^57\cdot e^{-0{,}2x}dx\$
	↓	Ziehe die 7 als Skalar vor das Integral
	$=$	$\displaystyle 7\int_0^5e^{-\frac{1}{5}x}dx$
	↓	Integriere
	$=$	$\displaystyle 7\cdot(-5)[e^{-\frac{1}{5}x}]_0^5$
	↓	Werte an den Grenzen aus
	$=$	$\displaystyle -35\cdot(e^{-1}-e^0)=35-\frac{35}{e} \ \text{FE}$

Damit gilt für den Anteil des Flächenstücks des Rechtecks am Inhalt des Flächenstücks:

\displaystyle f'(x)=7\cdot(-0{,}2)\cdot e^{-0{,}2\cdot x}=-1{,}4\cdot e^{-0{,}2\cdot x}<0

Also ist der prozentuale Anteil gerade 58 %.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.