Das Newton-Verfahren dient zur Annäherung an Nullstellen; durch das immer wieder neu Einsetzen des Ergebnisses in die Newton-Formel nähert man die Nachkommastellen der Nullstelle immer mehr an. Diese Art von Verfahren nennt man Iterationsverfahren.
Iterationsformel:
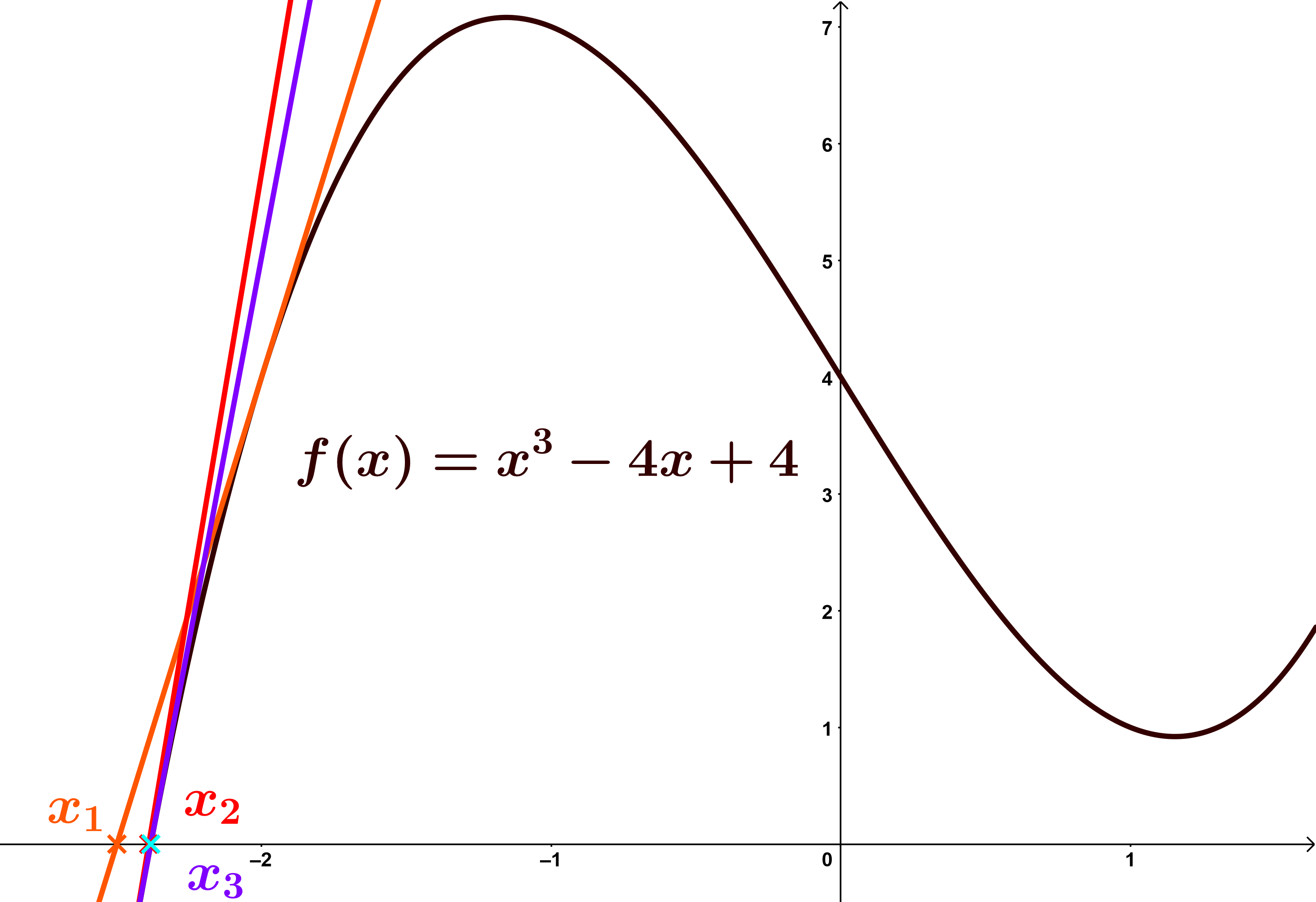
Das Newton-Verfahren
Da gewisse Nullstellen nicht genau bestimmbar sind, wird das Newton-Verfahren eingesetzt, um Nullstellen anzunähern. Um diese zu berechnen, benötigst du die Ableitung.
Beispiel:
Nullstelle von
Überprüfe, ob du nicht andere Lösungswege benutzen kannst!
Dies bedeutet, dass Ergebnisse eines Schrittes wieder als Ausgangswert für den jeweils nächsten Schritt genommen werden. Dies kannst du in der Graphik mit der Rechenmaschine erkennen.
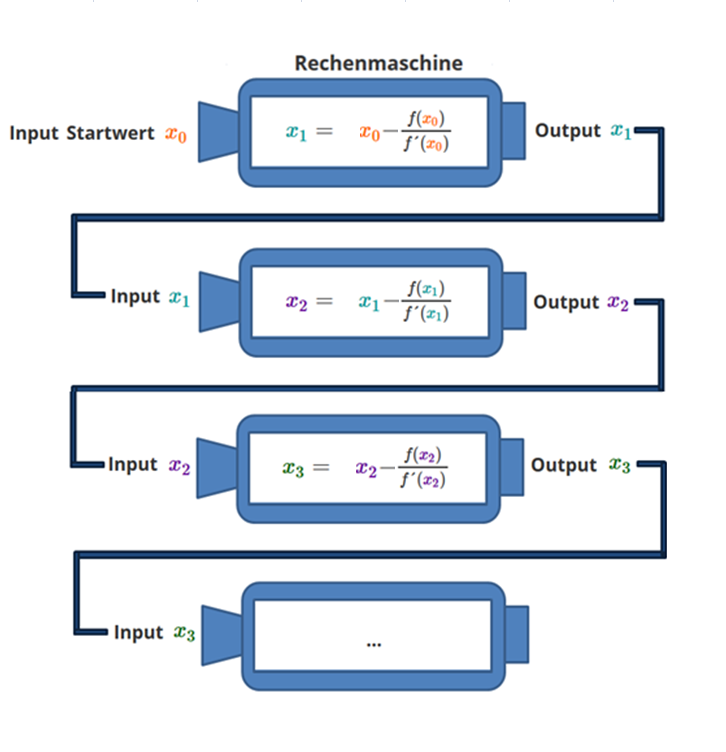
Beispiel:
So erhältst du :
Falls du ein Intervall gegeben hast, in dem deine Nullstelle liegt, bietet es sich an, die Mitte des Intervalls zu wählen
Beispiel: Die Nullstelle liegt im Intervall Wähle also
Falls kein Intervall gegeben ist, kannst du durch eine Wertetabelle bestimmen, eine Skizze kann dir ebenfalls helfen, notfalls kannst du auch raten. Das Newton-Verfahren kann aber auch schiefgehen, wenn du als eine Extremstelle wählst. Falls dein sehr weit von der Nullstelle entfernt ist, brauchst du sehr, sehr viele Iterationsschritte. Du versuchst also dein möglichst nahe der Nullstelle zu wählen.
Bestimmung von durch eine Wertetabelle:
Lege eine Wertetabelle der Funktion an, mit - Werten, in deren Umgebung du die Nullstelle vermutest. (Eine Skizze hilft dir.)
Suche nach einem Vorzeichenwechsel der Funktionswerte.
Die Nullstelle liegt zwischen den -Werten, deren Funktionswerte einen Vorzeichenwechsel haben.
Beispiel:
-3 | -2 | -1 | 0 | 1 | 2 | 3 | |
-43 | -20 | -9 | -4 | 1 | 12 | 35 |
Vorzeichenwechsel im Intervall wähle z.B.
So erhältst du deine angenäherte Lösung:
Je länger du das Verfahren anwendest, desto näher kommst du an die Nullstelle. Ein Ziel deiner Näherung könnte sein, die ersten drei Nachkommastellen korrekt zu bestimmen. Wenn sich nach mehreren Iterationsschritten deine drei Nachkommastellen nicht mehr ändern, kannst du davon ausgehen, dass du am Ziel bist.
Beispiel:
Die Nullstelle liegt bei ca. .
Vereinfachung für den Taschenrechner
Ausführlicher Lösungsweg
Du benötigst | Ergebnis | Erhältst du durch |
|---|---|---|
Berechnen |
Wertetabelle:
Setze verschiedene Werte, für ein, um jeweils nach dem y-Wert aufzulösen. Trage dies anschließend in eine Wertetabelle ein und finde den Übergang vom Positiven/Negativen, diese zwei Punkte stellen dann dein Intervall dar. Beim Wählen beachte, dass keine Extremstelle darstellen darf.
Beispiel:
-7 |
Vorzeichenwechsel im Intervall wähle z.B. .
Ausführliches Beispiel
Berechnung | Erklärung |
|---|---|
Setze und in die Formel ein und berechne . | |
Setze und in die Formel ein und berechne . | |
Setze und in die Formel ein und berechne . | |
Setze und in die Formel ein. Und löse nach auf. |
ist die Annäherung der Nullstelle bis zur Nachkommastelle von
Übungsaufgaben
Laden
