Zeichnen im 3D-Koordinatensystem

Das dreidimensionale Koordinatensystem ist eine Erweiterung des zweidimensionalen Koordinatensystems um eine dritte Dimension. Es besteht aus drei Achsen, die den dreidimensionalen Raum symbolisieren. Sie werden mit ${\mathrm x}_1,\;{\mathrm x}_2\;\mathrm{und}\;{\mathrm x}_3$ bezeichnet, wobei ${\mathrm x}_1,\;{\mathrm x}_2$ die Grundfläche (Boden) und ${\mathrm x}_3$ die Höhe darstellen.

Die drei Achsen stehen jeweils senkrecht aufeinander, und ihr gemeinsamer Schnittpunkt ist der Nullpunkt des Koordinatensystems und wird auch Koordinatenursprung genannt.

Koordinatensystem zeichnen

Koordinatenachsen zeichnen

1.) ${\mathrm x}_{2\;}-$ und ${\mathrm x}_3-$ Achse zeichnen:

Diese stehen senkrecht zueinander und können direkt auf die Kästchenlinien gezeichnet werden.

Sie bilden zusammen ein zweidimensionales Koordinatensystem.

Man zeichnet dabei nur die positive Seite der Achsen, um später die Übersichtlichkeit zu behalten.

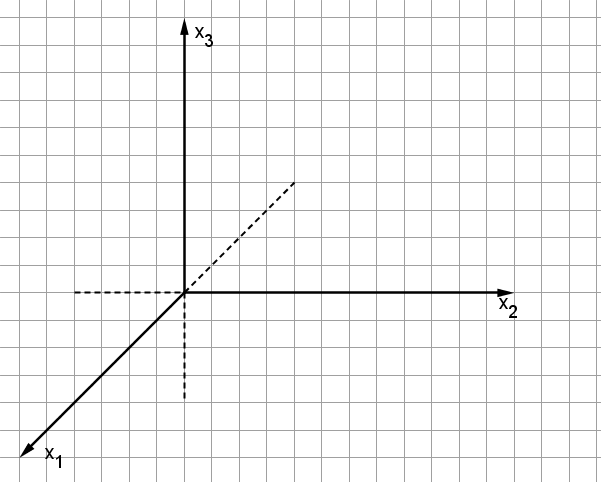
Geogebra File: https://assets.serlo.org/legacy/6148_5ofOsEfhPE.xml

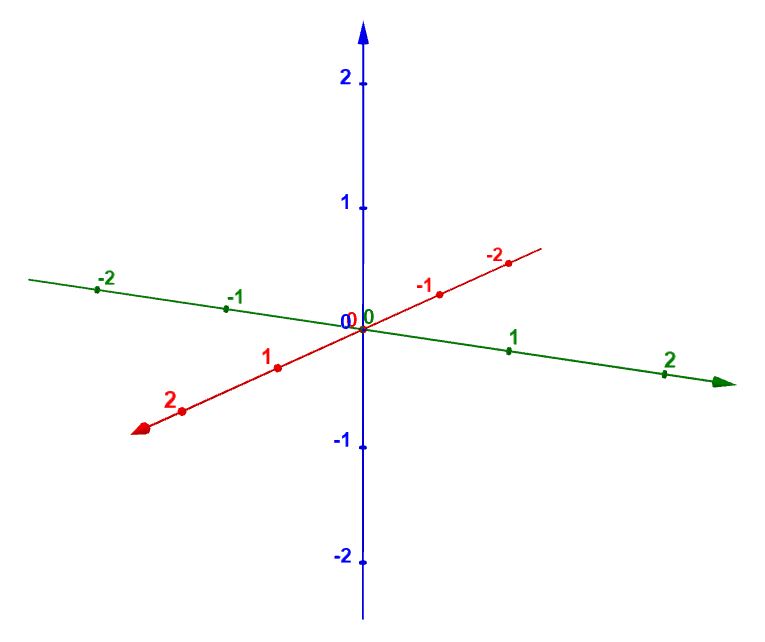
2.) ${\mathrm x}_1$ -Achse zeichnen:

Sie kann schräg nach vorne in einem beliebigen Winkel eingezeichnet werden.

Am einfachsten ist es allerdings, wenn sie in einem $45^\circ$ Winkel gezeichnet wird, da sie dann genau schräg durch die Kästchen verläuft.

Einheiten anzeichnen

3.) Einheiten an der ${\mathrm x}_{2\;}-$ und ${\mathrm x}_3-$ Achse einzeichnen: Im Normalfall wählt man diese gleich $1\;\text{cm}$ , wenn allerdings Punkte mit sehr großen Koordinaten eingezeichnet werden sollen, können die Einheiten auch kleiner oder größer gewählt werden.(z.B. $1\;\text{cm} = 2$ oder $1\;\text{cm} = 0{,}5$ )

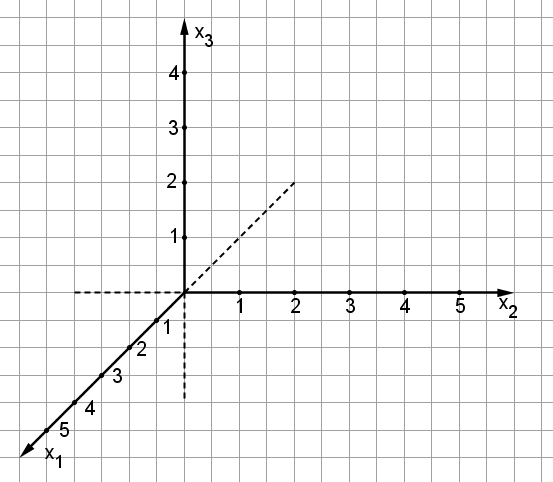
Geogebra File: https://assets.serlo.org/legacy/6150_h0UNkaJmIL.xml

4.) Einheiten an der ${\mathrm x}_1$ -Achse einzeichnen: Dabei ist ein schräges Kästchen auf der ${\mathrm x}_1$ -Achse genauso lang wie $2$ Kästchen auf den anderen beiden Achsen.

Punkte

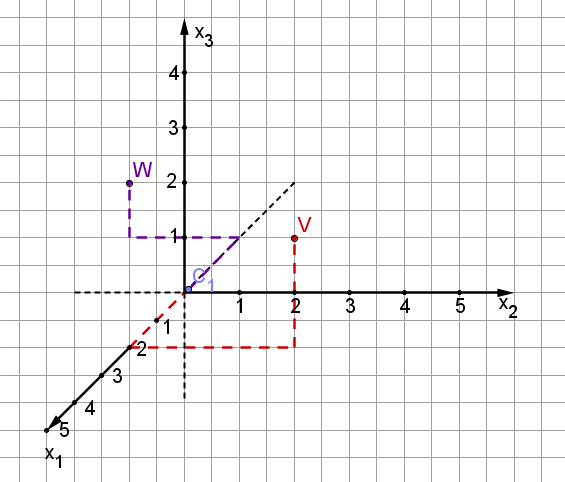
Dreidimensionale Punkte werden in der Form $\left(\left.{\mathrm x}_{1\;}\right|\;\left.x_{2\;}\right|\;{\mathrm x}_3\right)$ angegeben. Dabei repräsentieren die Einträge jeweils die Längen auf der entsprechenden Achse. Man geht also den ${\mathrm x}_1$ -Wert nach vorne, den ${\mathrm x}_2$ -Wert nach rechts und den ${\mathrm x}_3$ -Wert nach oben.

Beispiel:

$\mathrm V=\left(\left.2\;\right|\;\left.3\;\right|\;2\right)$

$2$ nach vorne

$3$ nach rechts

$2$ nach oben

$\mathrm W=\left(\left.-2\;\right|\;\left.-2\right|\;1\right)$

$2$ nach hinten ( $-2$ vorne)

$2$ nach links ( $-2$ rechts)

$1$ nach oben

Geogebra File: https://assets.serlo.org/legacy/6144_kgd0wnAVMn.xml

Vektoren

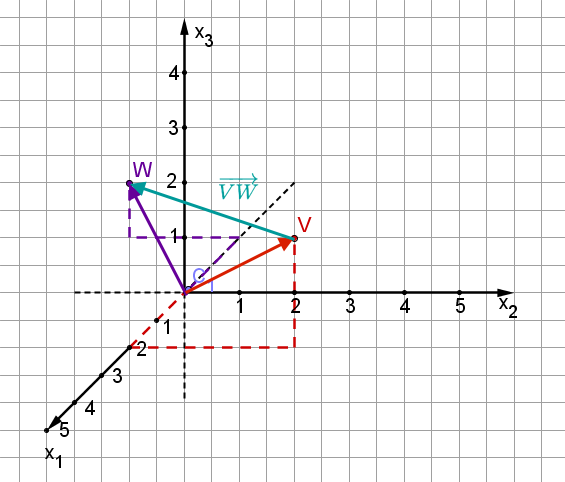
Ein Vektor ist ein Richtungspfeil und wird in der Form $\begin{pmatrix}{\mathrm x}_1\\{\mathrm x}_2\\{\mathrm x}_3\end{pmatrix}$ angegeben. Auch hier repräsentieren die Einträge jeweils die Längen auf den jeweiligen Achsen. Der so gefundenen Punkt repräsentiert den Endpunkt des Vektors. Allerdings geht man bei Vektoren von einem Anfangspunkt aus, der vom Nullpunkt verschieden sein kann. Wenn kein Anfangspunkt angegeben ist, geht man vom Nullpunkt aus.

Der Vektor wird durch einen Pfeil vom Anfangs zum Endpunkt repräsentiert.

Beispiel:

$\overrightarrow{\mathrm V}=\begin{pmatrix}2\\3\\2\end{pmatrix}, \overrightarrow{\mathrm W}=\begin{pmatrix}-2\\-2\\1\end{pmatrix}$

$\overrightarrow{\mathrm{VW}}=\begin{pmatrix}-2-2\\-2-3\\1-2\end{pmatrix}=\begin{pmatrix}-4\\-5\\-1\end{pmatrix}$

Geogebra File: https://assets.serlo.org/legacy/6142_UvTix7EwlQ.xml

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?