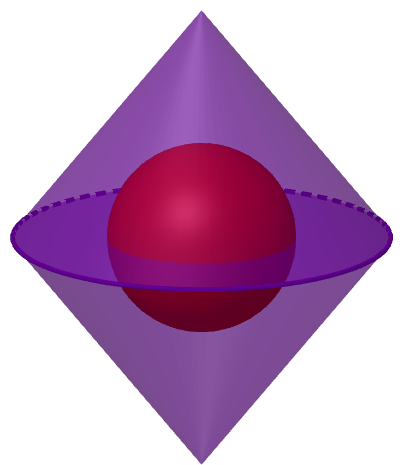
Gegeben ist ein Rotationskörper.
Zeichne seinen Axialschnitt.
Maße:
Kugelradius: ,
Kegelradius: ,
Kegelhöhe:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper
Der Rotationskörper
Der gegebene Rotationskörper besteht aus zwei , deren Grundflächen aufeinander liegen. Im Mittelpunkt des Rotationskörpers befindet sich eine .
Der Axialschnitt
Die folgende Tabelle zeigt die Zuordnung zwischen einem Rotationskörper und dem dazugehörenden Axialschnitt.
Rotationskörper | Axialschnitt |
|---|---|
Kegel | gleichschenkliges Dreieck |
Kugel | Kreis |
Axialschnitt der Kugel
Zeichne zunächst die Symmetrieachse als senkrechte Gerade.
Wähle einen Punkt auf dieser Geraden. Dieser Punkt ist der Mittelpunkt des Kreises (Axialschnitt der Kugel).
Zeichne einen Kreis um mit dem Radius .

Axialschnitt des Doppelkegels
Jeder der beiden Kegel hat einen Radius von und eine Höhe von . Als Axialschnitt musst du zwei gleichschenklige Dreiecke zeichnen.
Konstruiere zuerst die Basis der beiden gleichschenkligen Dreiecke.
Zeichne eine Gerade senkrecht zur Symmetrieachse durch den Punkt .
Zeichne um einen Kreis mit dem Radius (das ist der Kegelradius). Der Kreis schneidet die Gerade in den Punkten und .
Die Strecke ist die Basis der beiden gleichschenkligen Dreiecke.

Zur besseren Übersichtlichkeit werden einige Hilfslinien entfernt.
Konstruktion der Höhe der beiden gleichschenkligen Dreiecke.
Zeichne um einen Kreis mit dem Radius (das ist die Kegelhöhe).
Der Kreis schneidet die Symmetrieachse in den Punkten und . Verbinde mit und mit . Verbinde ebenso mit und mit .
Im Axialschnitt ist der Teil der Strecke nicht sichtbar, der durch die Kugel verläuft. Außerdem werden zur besseren Übersichtlichkeit alle Hilfslinien und Punkte entfernt.

Der Axialschnitt des Rotationskörpers ist fertig.

Bei dem dargestellten Körper handelt es sich um einen Rotationskörper. Die Achse, um die sich die Figur dreht, nennt man Rotationsachse. Schneidet man einen Rotationskörper längs seiner Achse durch, erhält man den Axialschnitt des Körpers.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
