Der Höhensatz und Kathetensatz des Euklid beschreiben Größenverhältnisse im rechtwinkligen Dreieck.
Die Sätze bilden mit dem Satz des Pythagoras die Satzgruppe des Pythagoras.
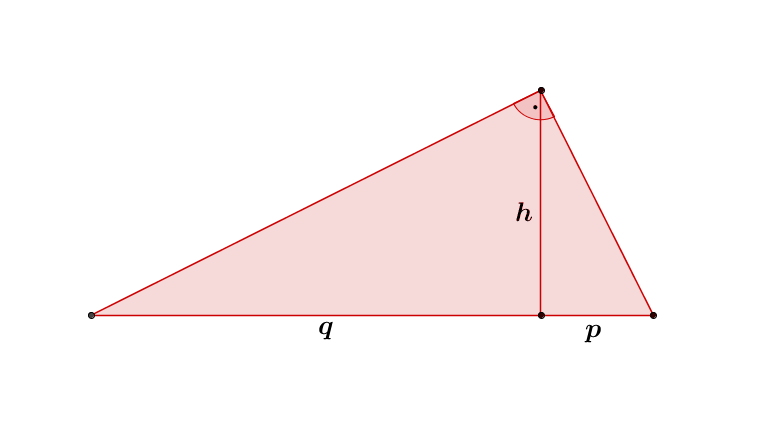
Höhensatz
Durch die Höhe wird die Hypotenuse in die Abschnitte und geteilt.
Der Höhensatz besagt, dass das Quadrat der Höhe gleich dem Produkt der Abschnitte der Hypotenuse und ist.
Formel:
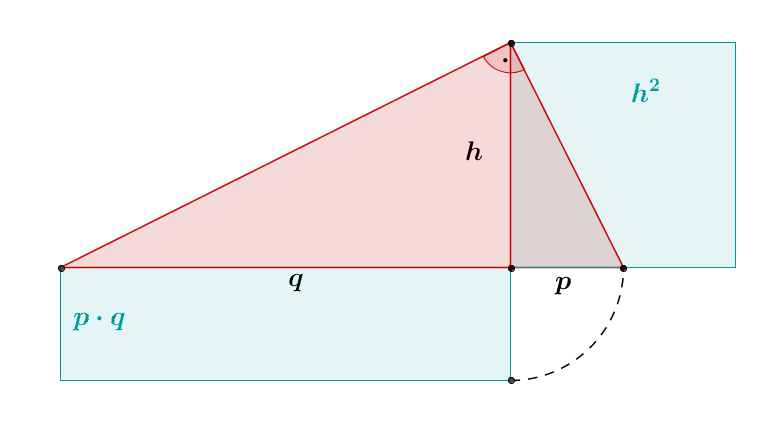
Alternative Darstellung
Höhensatz: Beispiel
Gegeben ist ein rechtwinkliges Dreieck mit und . Bestimme die Höhe .
Benutze dazu die Formel:
Allgemein | Beispiel |
|---|---|
Setze für und ein. | |
Rechne. | |
Ziehe die Wurzel. | |
Runde (falls verlangt). |
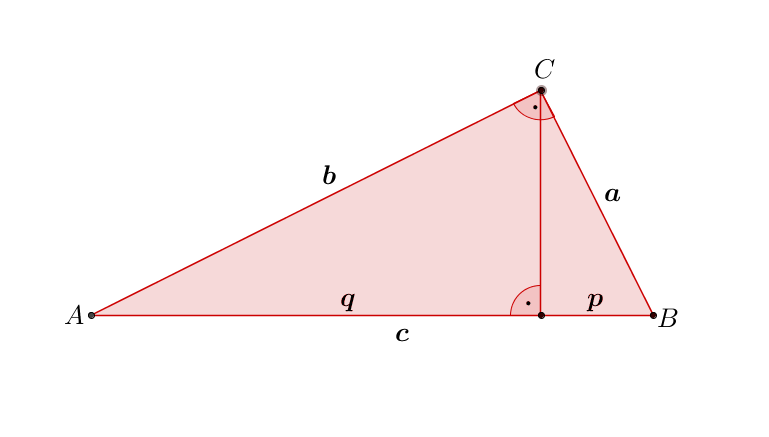
Kathetensatz
Der Kathetensatz besagt, dass jeweils das Quadrat einer Kathete gleich dem Produkt des anliegenden Achsenabschnitts der Hypotenuse und der Hypotenuse selbst ist.
Formel:
Kathetensatz: Beispiel
Gegeben ist ein rechtwinkliges Dreieck mit und . Bestimme die Katheten und .
Allgemein | Beispiel |
|---|---|
Berechne die an anliegende Kathete mit der Formel . | |
Setze für und ein. | |
Ziehe die Wurzel. | |
Berechne aus und durch Subtraktion. | |
Setze für und ein und rechne. | |
Berechne die an anliegende Kathete mit der Formel . | |
Setze für und ein. | |
Ziehe die Wurzel. | |
Lösung: | und . |
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
