Für diese Aufgabe benötigst du Kenntnisse über die Eigenschaften von Prismen. Die Grundfläche und die Deckfläche begrenzen jeweils $6$ Kanten. Außerdem verlaufen $6$ Kanten von den Ecken der Grundfläche zu den Ecken der Deckfläche.

$6\ Kanten+6\ Kanten+6\ Kanten=18\ Kanten$

Deshalb lautet die Antwort: Ein Prisma, dessen Grundfläche ein Sechseck ist, hat $18$ Kanten.

Gegeben ist folgende Aussage: "Anzahl der Ecken" + "Anzahl der Flächen" - "Anzahl der Kanten" $= 2$ Außerdem haben wir ein Prisma mit fünfeckiger Grundfläche gegeben. Anhand der Abbildung zählst du nun die Ecken, Flächen und Kanten.

Anzahl der Ecken $= 10$ Anzahl der Flächen $= 7$ Anzahl der Kanten $= 15$

Zum Schluss setzt du die Werte in die Gleichung ein und rechnest die linke Seite der Gleichung aus.

"Anzahl der Ecken" + "Anzahl der Flächen" - "Anzahl der Kanten" $= 10 + 7 - 15 = 2$

Somit stimmt die Gleichung für ein Prisma, dessen Grundfläche ein Fünfeck ist.

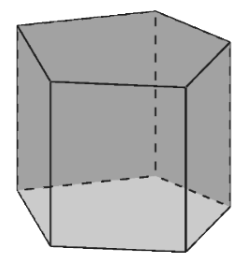
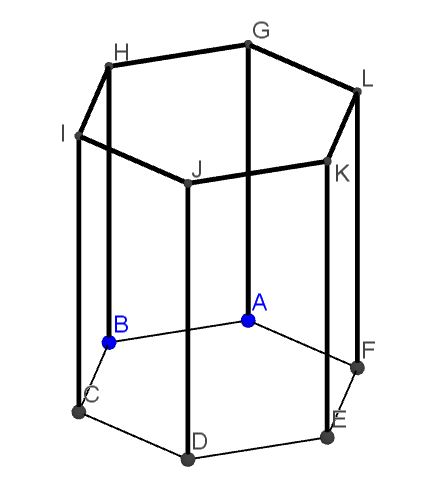
Bei dieser Teilaufgabe sollst du die Abbildung des Prismas mit der fünfeckigen Grundfläche zur Hilfe. Ausgehend von dieser Abbildung kannst du dir überlegen wie viele Ecken, Flächen und Kanten ein Prisma mit einer n-eckigen Grundfläche hat.

Gegeben ist wieder die Gleichung aus Teilaufgabe 2)

"Anzahl der Ecken" + "Anzahl der Flächen" - "Anzahl der Kanten" = 2

Zunächst überlegst du dir, wie viele Ecken ein Prismas mit n-eckiger Grundfläche hat. Wir wissen, dass ein Prisma mit fünfeckiger Grundfläche $10$ Ecken hat. Und zwar die $5$ Ecken der Grundfläche und die $5$ Ecken der Deckfläche, da die Grundfläche und die Deckfläche deckungsgleich sind.

Also hat ein Prisma mit n-eckiger Grundfläche $n+n = 2n\;$ Ecken.

Nun überlegst du dir, wie viele Flächen ein Prisma mit n-eckiger Grundfläche hat. Jedes Prisma hat eine Grundfläche und eine Deckfläche. Zu diesen beiden Flächen kommen noch die einzelnen Flächen der Mantelfläche. Bei einem Prisma mit fünfeckiger Grundfläche besteht die Mantelfläche aus $5$ einzelnen Flächen.

Insgesamt hat ein Prisma mit n-eckiger Grundfläche also $2+n\;$ Flächen.

Zum Schluss überlegst du dir noch, wie viele Kanten ein Prisma mit n-eckiger Grundfläche besitzt. Hier hilft dir auch die Teilaufgabe a). Dort hast du dir überlegt, wie viele Kanten ein Prisma mit sechseckiger Grundfläche hat, und zwar begrenzen $6$ Kanten die Grundfläche und $6$ Kanten die Deckfläche. Außerdem verläuft jeweils eine Kante von jeder Ecke der Grundfläche zu einer Ecke der Deckfläche. Folglich hat die Mantelfläche auch $6$ Kanten.

Also hat ein Prisma mit n-eckiger Grundfläche $n+n+n = 3n\;$ Kanten.

Zum Schluss setzt du noch die Teilergebnisse in die gegebene Gleichung und vereinfachst die linke Seite.

"Anzahl der Ecken" + "Anzahl der Flächen" - "Anzahl der Kanten" = $2n+(2+n)-3n= 2n + 2 +n - 3n= 3n - 3n +2 = 2$

Im letzten Schritt siehst du, dass tatsächlich $2$ herauskommt.