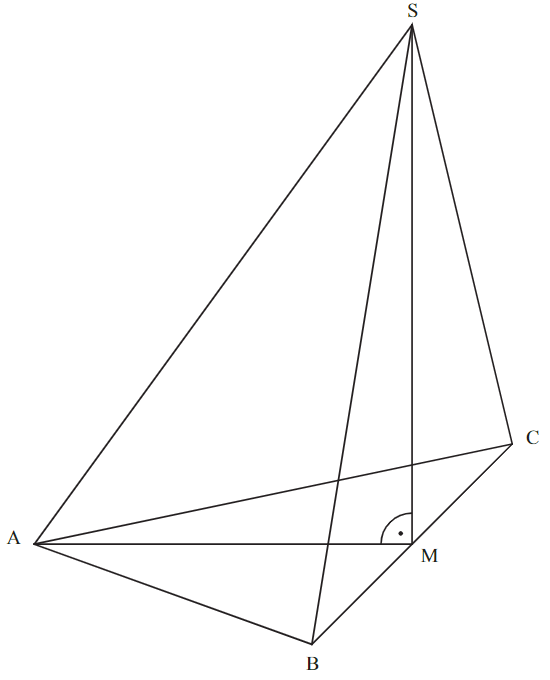
A 2.0 Das gleichschenklige Dreieck $ABC$ mit der Basis $\left[BC\right]$ ist die Grundfläche der Pyramide $ABCS$. Die Spitze $S$ liegt senkrecht über dem Mittelpunkt $M$ der Basis $\left[BC\right]$(siehe Zeichnung). Es gilt: $\overline{BC}=12cm$; $\overline{AM}=8cm$ ; $\overline{MS}=11cm$. Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

A 2.1 Berechnen Sie die Länge der Strecke $\overline{AS}$ und das Maß $\phi$ des Winkels $ASM$. [Ergebnisse: $\overline{AS}=\mathrm{13,60}cm;\phi =\mathrm{36,03}°$]

A 2.2 Die Strecke $[PQ]$ mit $P\in [BS]$ und $Q\in [CS]$ ist parallel zur Strecke $[BC]$. Der Punkt $D$ ist der Mittelpunkt der Strecke $[PQ]$ mit $\overline{MD}=4cm$. Zeichnen Sie die Strecke $[PQ]$ in das Schrägbild zu A 2.0 ein und berechnen Sie deren Länge. [Ergebnis: $\overline{PQ}=\mathrm{7,64}cm$]

A 2.3 Punkte $R_n$ auf der Strecke $[AS]$ mit $\overline{A{R}_n}(x)=x$ cm $(x<\mathrm{13,60};x\in {ℝ}_{\mathrm{𝟘}}^{\text{+}})$ bilden zusammen mit den Punkten $P$ und $Q$ Dreiecke $PQ{R}_n$.

Zeichnen Sie das Dreieck $PQ{R}_1$ für $x=9$ in das Schrägbild zu A 2.0 ein und bestimmen Sie sodann durch Rechnung das Maß $\delta$ des Winkels $SD{R}_1$.

[Teilergebnis: $\overline{D{R}_1}=\mathrm{4,25}$ cm]

A 2.4 Das Dreieck $PQS$ ist die Grundfläche von Pyramiden $PQS{R}_n$.

Zeichnen Sie die Höhe $h$ der Pyramide $PQS{R}_1$ mit dem Höhenfußpunkt $F_1$ in das Schrägbild zu A 2.0 ein. Ermitteln Sie sodann die Länge der Strecken [$R_n{F}_n$] der Pyramiden $PQS{R}_n$ in Abhängigkeit von $x$.