Die vorgelegte Funktion $f$ist eine echt gebrochen rationale Funktion mit dem Nenner $x^2-4$. Die Nullstellen des Nenners sind $x_1=-2\vee x_2=2$. Da der Zähler hier keine Nullstellen hat, liegen Polstellen vor.

Somit lauten die Gleichungen der senkrechten Asymtoten:

$a_{S1}:x=-2$ und $a_{S2}:x=2$.

Der Zählergrad der gebrochen rationalen Funktion ist $1$ und der Nennergrad ist $2.$ Somit ist die $x-$Achse waagerechte Asymptote.

Oder ausführlicher:

$${\displaystyle f(x)=6\cdot \frac{x}{x^2-4}⟺f(x)=6\cdot \frac{x}{x\cdot (x-\frac{4}{x})}⟺f(x)=6\cdot \frac{1}{(x-\frac{4}{x})}\Rightarrow \underset{x\to \pm \infty }{\lim }f(x)=0}$$

Das Monotonieverhalten wird mittels des Vorzeichens der 1. Ableitung bestimmt.

$\begin{array}{l}f(x)=6\cdot \frac{x}{x^2-4}\\ \Rightarrow f^{\prime }(x)=6\cdot \frac{x^2-4-x\cdot 2x}{(x^2-4{)}^2}\\ \Rightarrow f^{\prime }(x)=-6\cdot \frac{x^2+4}{(x^2-4{)}^2}\end{array}$

Also gilt $f^{\prime }(x)<0$ für alle $x\in D_f$.

Somit ist f streng monoton fallend in $]-\infty ;-2]$, sowie in $]-2;2[$ und $]2;\infty [$.

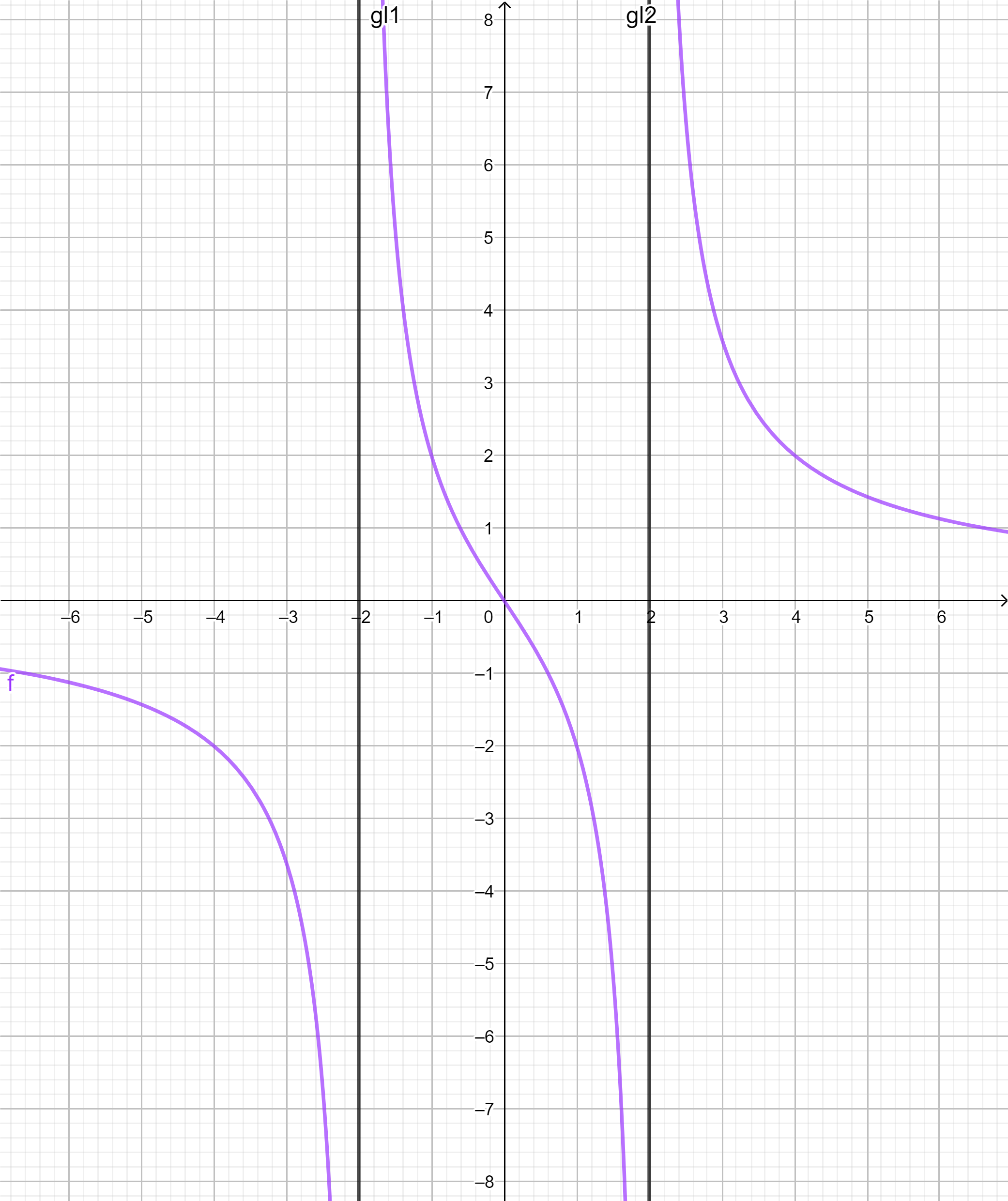
Die Punkte $A$und $B$ liegen auf dem Graph von $f.$Die Koordinaten der Punkte sind $A(3|(f3))$ und $B(8|f(8))$.

Es war angegeben: $A(3|\mathrm{3,6})$ und $B(8|\mathrm{0,8})$.

Es werden zwei Varianten der Lösung angegeben.

Variante 1:

Man berechnet die Maßzahl der Fläche zwischen der Strecke $[AB]$ und dem Graph$G_f$ im Intervall [3;8].

Bestimmung der Gleichung der Geraden $g_{AB}$ durch die Punkte $A$ und $B.$

Eine Geradengleichung hat die Form $y=m\cdot x+b$, wobei $m$ die Steigung der Geraden ist und $b$ der $y-$Achsenabschnitt.

Die Steigung $m$ ermittelt man mit Hilfe des Steigungsdreiecks.

$m={\displaystyle \frac{\frac{18}{5}-\frac{4}{5}}{8-3}}={\displaystyle \frac{-\frac{14}{5}}{5}}=-\frac{14}{25}$

Damit gilt: $g_{AB}:y=-\frac{14}{25}\cdot x+b$

Der Punkt $A$ liegt auf der Geraden: $${\displaystyle \frac{18}{5}=-\frac{14}{25}\cdot 3+b\Rightarrow b=\frac{90}{25}+\frac{42}{25}=\frac{132}{25}\Rightarrow y=-\frac{14}{25}\cdot x+\frac{132}{25}}$$

$\begin{array}{l}{A}_{\text{Fläche}}={\int }_3^8(-\frac{14}{25}\cdot x+\frac{132}{25}-6\cdot \frac{x}{x^2-4})dx\\ ⟺A_{\text{Fläche}}={\int }_3^8(-\frac{14}{25}\cdot x+\frac{132}{25}-3\cdot \frac{2x}{x^2-4})dx\\ ⟺A_{\text{Fläche}}=\frac{1}{2}\cdot (-\frac{14}{25}{x}^2)+\frac{132}{25}x-3\cdot \ln |x^2-4|){]}_3^8\\ ⟺A_{\text{Fläche}}=-\frac{7}{25}\cdot 64+\frac{132}{25}\cdot 8-3\cdot \ln 60-[-\frac{7}{25}\cdot 9+\frac{132}{25}\cdot 3-3\cdot \ln 5]\\ ⟺A_{\text{Fläche}}=-\frac{7}{25}\cdot 55+\frac{132}{25}\cdot 5-3(\ln 60-\ln 5)\\ ⟺A_{\text{Fläche}}=-\frac{7}{5}\cdot 11+\frac{132}{5}-3\cdot \ln 12=-\frac{77}{5}+\frac{132}{5}-3\cdot \ln 12\\ A_{\text{Fläche}}=\frac{55}{5}-3\cdot \ln 12=11-3\cdot \ln 12FE\end{array}$

Variante 2:

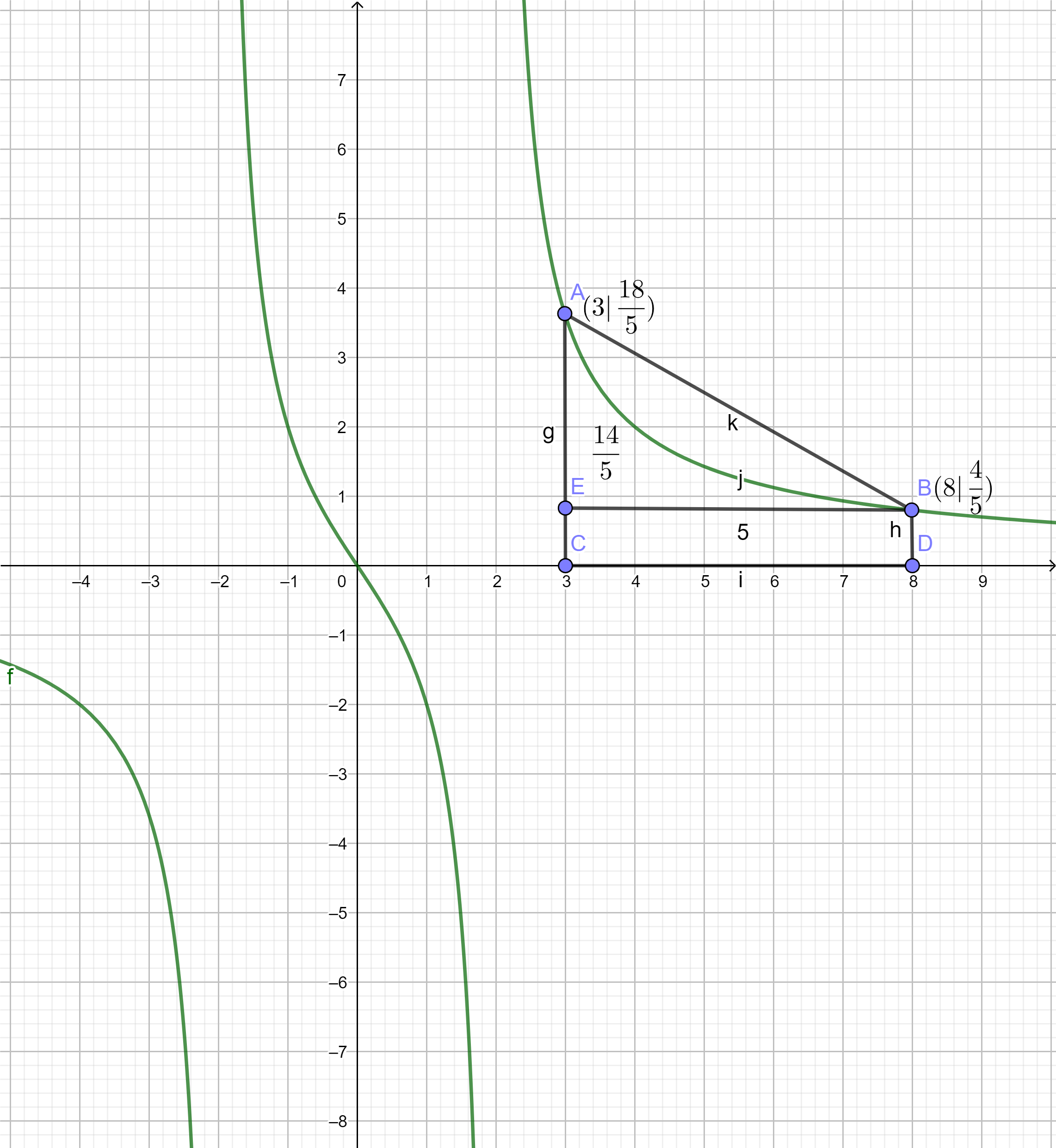
Man betrachtet die Skizze des Graphen von $f$ mit der Strecke $[AB]$.

Man erkennt, dass die Fläche zwischen der Strecke $[AB]$ und dem Intervall $[3;8]$ ein Viereck ist, das man in ein Rechteck und Dreieck zelegen kann.

Somit ist der Inhalt dieses Vierecks leicht zu berechnen.

Die Maßzahl der Fläche zwischen dem Graphen von $f$ und dem intervall $[3;8]$ wird mit Hilfe der logarithmischen Integration berechnet.

An der Skizze liest man ab, dass der Inhalt des Rechteckes $EBDC$ gerade $4FE$ und der Inhalt des Dreiecks $AEB$ gerade $\frac{1}{2}\cdot \frac{14}{5}\cdot 5=7FE$.

Zusammen ist der Inhalt des Viereckes $ABDC$ gerade $11FE.$

Berechnung der Maßzahl der Fläche zwischen $G_f$ und dem Intervall $[3;8]$:

$\begin{array}{l}A={\int }_3^{8}6\cdot \frac{x}{x^2-4}dx=3\cdot {\int }_3^8\frac{2x}{x^2-4}dx=3\cdot \ln |x^2-4|{]}_3^8\\ ⟺A=3\cdot [\ln 60-\ln 5]=3\cdot \ln 12FE\end{array}$

Insgesamt ergibt sich für die Maßzahl der Fläche zwischen der Strecke $[AB]$und $G_f$ der Wert $A_{\text{Fläche}}=11-3\cdot \ln 12\text{FE}$

Meiner Meinung nach liegen die Rechenvorteile der Variante 2 auf der Hand.