Analysis, Teil B, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
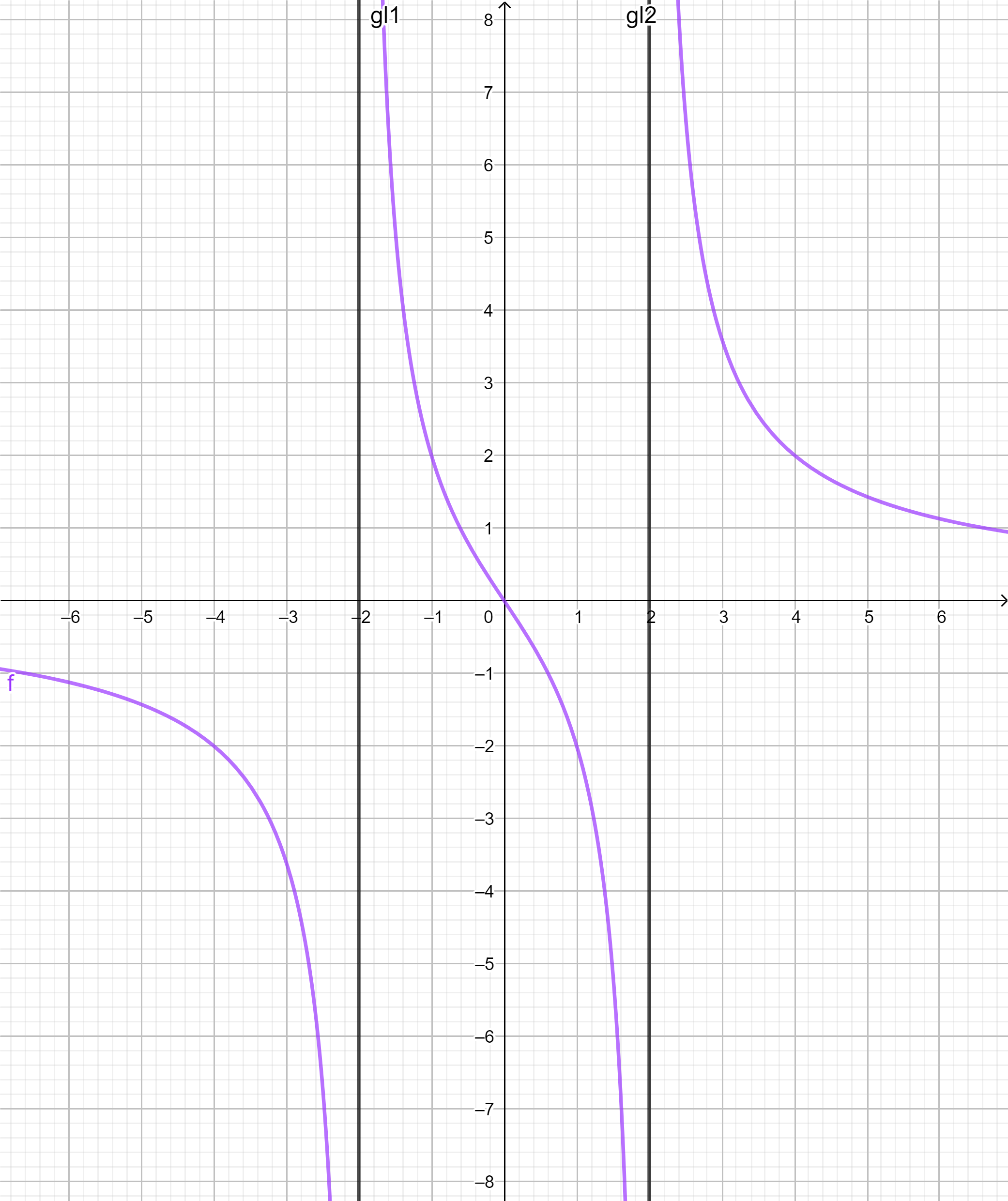
Gegeben ist die in $\mathbb{R}$ \{ $- 2; 2$ } definierte Funktion $f:x\mapsto\dfrac{6x}{x^2-4}$ . Der Graph von $f$ wird mit $G_{f}$ bezeichnet und ist symmetrisch bezüglich des Koordinatenursprungs.
1. Geben Sie die Gleichungen aller senkrechten Asymptoten von $G_{f}$ an. Begründen Sie, dass $G_{f}$ die x-Achse als waagrechte Asymptote besitzt. (3P)
  
  Die vorgelegte Funktion $f$ ist eine echt gebrochen rationale Funktion mit dem Nenner $x^{2} - 4$ . Die Nullstellen des Nenners sind $x_1=-2\lor x_2=2$ . Da der Zähler hier keine Nullstellen hat, liegen Polstellen vor.
  Somit lauten die Gleichungen der senkrechten Asymtoten:
  $a_{S1}:x=-2$ und $a_{S2}:x=2$ .
  Der Zählergrad der gebrochen rationalen Funktion ist $1$ und der Nennergrad ist $2.$ Somit ist die $x -$ Achse waagerechte Asymptote.
  Oder ausführlicher:
  $\displaystyle f(x)=6\cdot \frac{x}{x^2-4}\iff f(x)=6\cdot \frac{x}{x\cdot (x-\frac{4}{x})}\\\iff f(x)=6\cdot \frac{1}{(x-\frac{4}{x})}\\\Rightarrow \lim_{x\to\pm\infty} f(x)=0$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimmen Sie das jeweilige Monotonieverhalten von $f$ in den drei Teilintervallen
  $] - \infty -; 2, []−∞ −;2, [$ , $] - 2; 2 [$ und $]2;- \infty[$ der Definitionsmenge. Berechnen Sie zudem die Steigung der Tangente an $G_{f}$ im Punkt $(0 ∣ f (0))$ . (5P)
  (zur Kontrolle: $f'(x)=-\dfrac{6\cdot(x^2+4)}{(x^2-4)^2}$ )
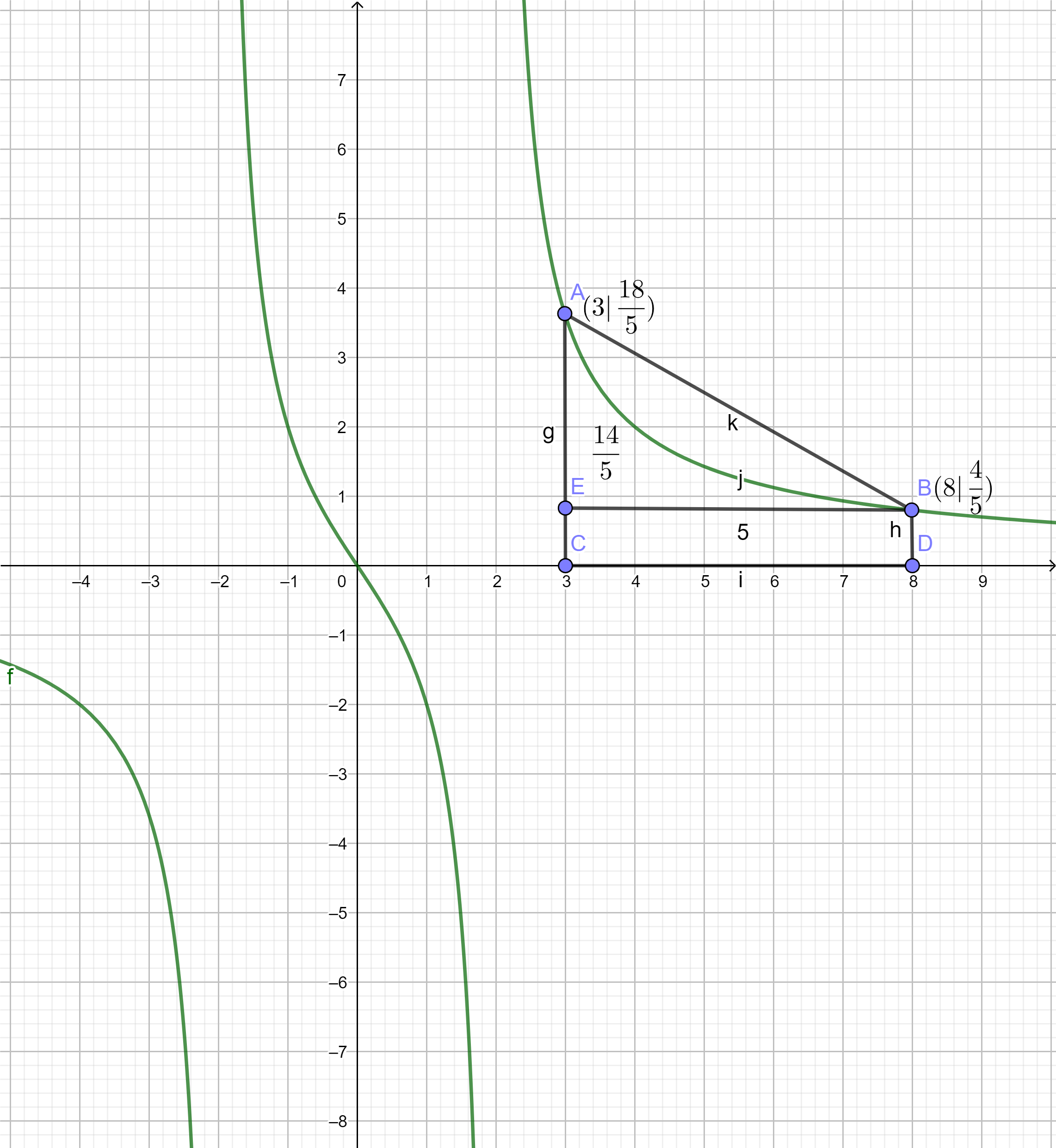
  Die Punkte $A (3 ∣ 3,6)$ und $B (8 ∣ 0,8)$ liegen auf $G_{f}$ ; zwischen diesen beiden Punkten verläuft $G_{f}$ unterhalb der Strecke $[A B]$ .
  
  Das Monotonieverhalten wird mittels des Vorzeichens der 1. Ableitung bestimmt.
  $f(x)=6\cdot \frac{x}{x^2-4}\\\Rightarrow f'(x)=6\cdot \frac{x^2-4-x\cdot 2x}{(x^2-4)^2}\\\Rightarrow f'(x)=-6\cdot \frac{x^2+4}{(x^2-4)^2}$
  Also gilt $f^{'} (x) < 0$ für alle $x\in D_f$ .
  Somit ist f streng monoton fallend in $]-\infty;-2]$ , sowie in $] - 2; 2 [$ und $]2;\infty[$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Skizzieren Sie $G_{f}$ im Bereich $-10 \leq x \leq10$ unter Verwendung der bisherigen Informationen in einem Koordinatensystem. (4P)
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Berechnen Sie den Inhalt der Fläche, die von $G_{f}$ und der Strecke $[A B]$ eingeschlossen wird. (5P)
  
  Die Punkte $A$ und $B$ liegen auf dem Graph von $f .$ Die Koordinaten der Punkte sind $A (3 ∣ (f 3))$ und $B (8 ∣ f (8))$ .
  Es war angegeben: $A (3 ∣ 3,6)$ und $B (8 ∣ 0,8)$ .
  Es werden zwei Varianten der Lösung angegeben.
  Variante 1:
  Man berechnet die Maßzahl der Fläche zwischen der Strecke $[A B]$ und dem Graph $G_{f}$ im Intervall [3;8].
  Bestimmung der Gleichung der Geraden $g_{AB}$ durch die Punkte $A$ und $B .$
  Eine Geradengleichung hat die Form $y=m\cdot x+b$ , wobei $m$ die Steigung der Geraden ist und $b$ der $y -$ Achsenabschnitt.
  Die Steigung $m$ ermittelt man mit Hilfe des Steigungsdreiecks.
  $m=\dfrac{\frac{18}{5}-\frac{4}{5}}{8-3}=\dfrac{-\frac{14}{5}}{5}=-\frac{14}{25}$
  Damit gilt: $g_{AB}:y=-\frac{14}{25}\cdot x+b$
  Der Punkt $A$ liegt auf der Geraden: $\displaystyle \frac{18}{5}=-\frac{14}{25}\cdot 3+b\\\Rightarrow b=\frac{90}{25}+\frac{42}{25}=\frac{132}{25}\\\Rightarrow y=-\frac{14}{25}\cdot x+\frac{132}{25}$
  $A_{\text{Fläche}}=\int_3^8(-\frac{14}{25}\cdot x+\frac{132}{25}-6\cdot \frac{x}{x^2-4})dx\\ \iff A_{\text{Fläche}}=\int_3^8(-\frac{14}{25}\cdot x+\frac{132}{25}-3\cdot \frac{2x}{x^2-4})dx\\ \iff A_{\text{Fläche}}=\frac{1}{2}\cdot (-\frac{14}{25}x^2)+\frac{132}{25} x-3\cdot \ln|x^2-4|)]_3^8\\ \iff A_{\text{Fläche}}=-\frac{7}{25}\cdot 64+\frac{132}{25}\cdot 8-3\cdot \ln60-[-\frac{7}{25}\cdot 9+\frac{132}{25}\cdot 3-3\cdot \ln5]\\ \iff A_{\text{Fläche}}=-\frac{7}{25}\cdot 55+\frac{132}{25}\cdot 5-3(\ln60-\ln5)\\ \iff A_{\text{Fläche}}=-\frac{7}{5}\cdot 11+\frac{132}{5}-3\cdot \ln 12=-\frac{77}{5}+\frac{132}{5}-3\cdot \ln12\\ \ A_{\text{Fläche}}=\frac{55}{5}-3\cdot \ln 12=11-3\cdot \ln 12 FE$
  Variante 2:
  Man betrachtet die Skizze des Graphen von $f$ mit der Strecke $[A B]$ .
  Man erkennt, dass die Fläche zwischen der Strecke $[A B]$ und dem Intervall $[3; 8]$ ein Viereck ist, das man in ein Rechteck und Dreieck zelegen kann.
  Somit ist der Inhalt dieses Vierecks leicht zu berechnen.
  Die Maßzahl der Fläche zwischen dem Graphen von $f$ und dem intervall $[3; 8]$ wird mit Hilfe der logarithmischen Integration berechnet.
  An der Skizze liest man ab, dass der Inhalt des Rechteckes $E B D C$ gerade $4 F E$ und der Inhalt des Dreiecks $A E B$ gerade $\frac{1}{2}\cdot \frac{14}{5}\cdot 5=7 FE$ .
  Zusammen ist der Inhalt des Viereckes $A B D C$ gerade $11 F E .$
  Berechnung der Maßzahl der Fläche zwischen $G_{f}$ und dem Intervall $[3; 8]$ :
  $A=\int_3^86\cdot \frac{x}{x^2-4}dx=3\cdot\int_3^8\frac{2x}{x^2-4}dx=3\cdot \ln|x^2-4|]_3^8\\ \iff A=3\cdot [\ln60-\ln5]=3\cdot \ln12 FE$
  Insgesamt ergibt sich für die Maßzahl der Fläche zwischen der Strecke $[A B]$ und $G_{f}$ der Wert $A_{\text{Fläche}}=11-3\cdot \ln 12\, \text{FE}$
  Meiner Meinung nach liegen die Rechenvorteile der Variante 2 auf der Hand.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Betrachtet wird die Schar der Funktionen $f_{a,b,c}:x \mapsto \dfrac{ax+b}{x^2+c}$ mit $a,b,c \in \mathbb{R}$ und maximaler Definitionsmenge $D_{a,b,c}$ .
1. Die Funktion $f$ aus Aufgabe 1 ist eine Funktion dieser Schar. Geben Sie die zugehörigen Werte von $a, b$ und $c$ an. (1P)
  
  Die Funktion $f$ aus Aufgabe 1 hat den Funktionsterm $\frac{6\cdot x}{x^2-4}$
  Die Funktionenschar $f_{a,b,c}$ hat den Funktionsterm $\frac{ax+b}{x^2+c}\\\Rightarrow a=6\land b=0\land c=-4$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Begründen Sie: Wenn $a = 0$ und $b \neq0$ gilt, dann ist der Graph von $f_{a,b,c}$ symmetrisch bezüglich der y-Achse und schneidet die x-Achse nicht. (2P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
  $f_{0,b,c}(x)=\frac{b}{x^2+c}$
  Der Graph von $f_{0,b,c}$ ist symmetrisch zur $y -$ Achse, denn der Zähler $Z (x) = b$ ist als Konstante symmetrisch zur $y -$ Achse und der Nenner $N (x) = x^{2} + c$ ist als ganzrationale Funktion mit nur geraden Hochzahlen symmetrisch zur $y -$ Achse.
  Und somit ist der Quotient aus dem zur $y -$ Achse symmetrischen Zähler und Nenner symmetrisch zur $y -$ Achse.
  Oder $f_{0,bc}(x)=f_{0,b,c}(-x)\thinspace \forall x\in \mathbb{R}\iff \frac{b}{x^2+c}=\frac{b}{(-x)^2+c}$ wahr.
  Die Funktion schneidet die x-Achse nicht, da der Zähler wegen $b\neq 0$ nicht $0$ werden kann.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Geben Sie für $a, b$ und $c$ alle Werte an, sodass sowohl $D_{a,b,c}= \mathbb{R}$ gilt als auch, dass der Graph von $f_{a,b,c}$ symmetrisch bezüglich des Koordinatenursprungs, aber nicht identisch mit der x-Achse ist. (3P)
4. Für die erste Ableitung von $f_{a,b,c}$ gilt: $f'_{a,b,c}(x)=-\dfrac{ax^2+2bx-ac}{(x^2+c)^2}$ .
  Zeigen Sie: Wenn $a\neq0$ und $c \gt0$ gilt, dann besitzt der Graph von $f_{a,b,c}$ genau zwei Extrempunkte. (4P)
  
  Der Graph $f_{\left\{a,b,c\right\}}$ hat genau zwei Extrempunkte, wenn $f'_{\left\{a,b,c\right\}}$ zwei Nullstellen mit Vorzeichenwechsel hat.
  Das Vorzeichen von $f'_{\left\{a,b,c\right\}}$ wird vom Zählerterm von $f'_{\left\{a,b,c\right\}}\left(x\right)\$ bestimmt, da der Nennerterm als Quadrat positiv ist.
  Da $a\ne0$ vorausgesetzt ist, wird der Zählerterm durch eine Parabel graphisch dargestellt. Wenn der Zählerterm zwei verschiedene Nullstellen hat, so gibt es genau zwei Extrempunkte.
  $a\cdot x^2+2\cdot bx-a\cdot c=0\iff x^2+\frac{2b}{a}\cdot x-c=0\\\iff x^2+\frac{2b}{a}\cdot x=c\iff x^2+\frac{2b}{a}\cdot x+(\frac{b}{a})^2=c\\\iff (x+\frac{b}{a})^2=c+(\frac{b}{a})^2$
  Da $c > 0$ vorausgesetzt wurde ist die Summe $c+(\frac{b}{a})^2>0$ und es gibt zwei verschiedene Nullstellen von $f'_{a,b,c}$ :
  $x_1=-\frac{b}{a}+\sqrt{(\frac{b}{a})^2+c}$ und $x_2=-\frac{b}{a}-\sqrt{(\frac{b}{a})^2+c}$ .
  Damit hat $f_{a,b,c}$ genau zwei Extrempunkte.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
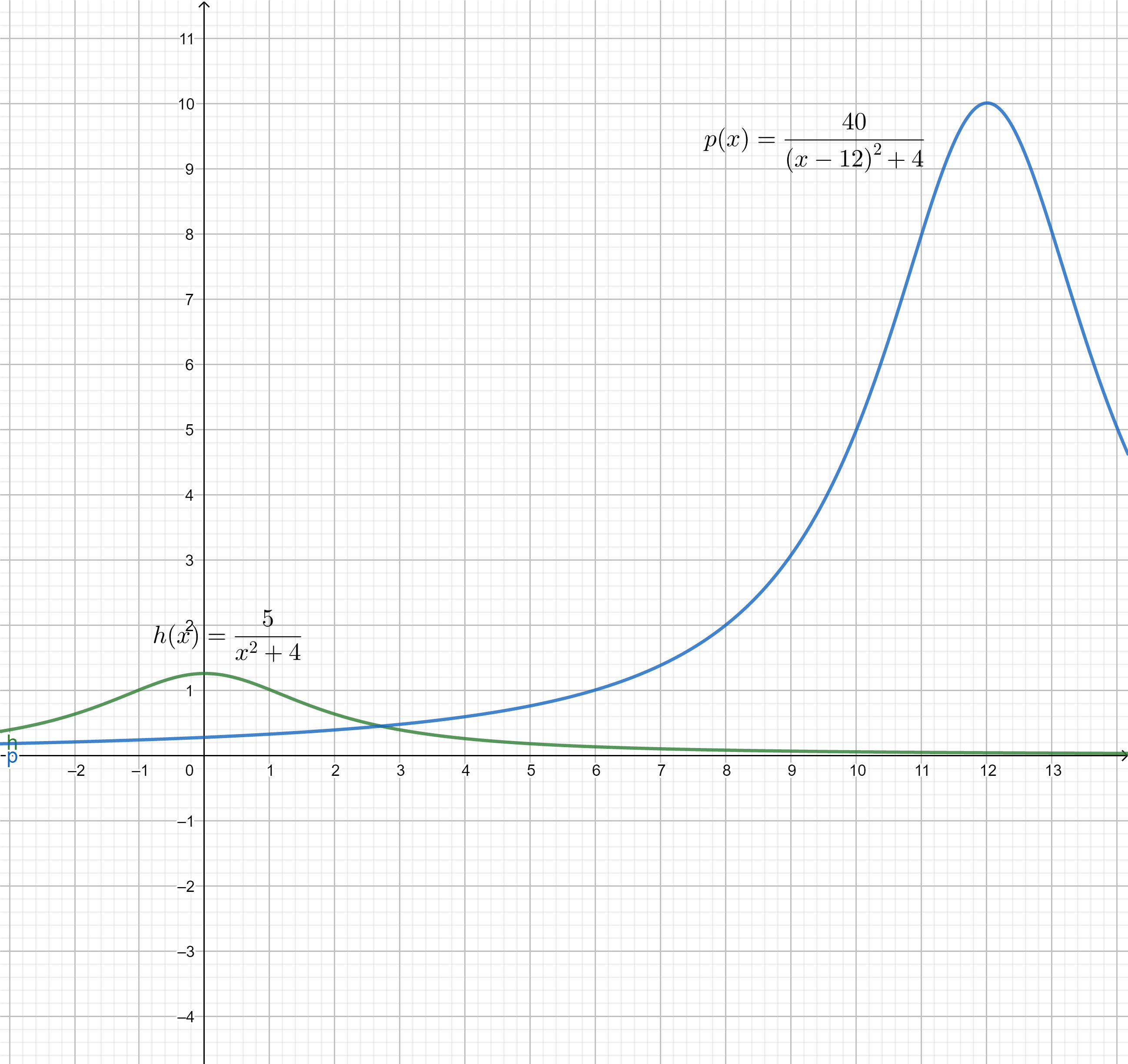
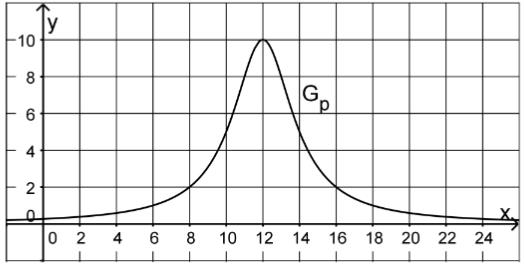
Betrachtet wird die in $\mathbb{R}$ definierte Funktion $p:x \mapsto\dfrac{40}{(x-12)^2+4}$ ; die Abbildung zeigt den Graphen $G_{p}$ von p.
1. Beschreiben Sie, wie $G_{p}$ aus dem Graphen der in $\mathbb{R}$ definierten Funktion $h:x\mapsto\dfrac{5}{x^2+4}$ schrittweise hervorgeht, und begründen Sie damit, dass $G_{p}$ bezüglich der Gerade mit der Gleichung $x = 12$ symmetrisch ist. (4P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsgraphen verändern
  Ausgehend vom Graphen $G_{h_{}}$ der Funktion $\displaystyle h(x)=\frac{5}{x^2+4}$ h soll der Graph $G_{p}$ der Funktion $\displaystyle p(x) =\frac{40}{(x-12)^2+4}$ dargestellt werden.
  Der Graph $G_{f}$ der Funktion $y = f (x - a); a > 0$ ergibt sich aus dem Graphen $G_{g}$ der Funktion $g (x) = f (x - a)$ durch Verschiebung um $a$ in Richtung der positiven $x -$ Achse.
  Beispiel: Der Graph der Funktion $f_{o} (x) = x^{2}$ ist die Normalparabel mit dem Scheitelpunkt $S_{o} (0 ∣ 0)$ und der Graph der Funktion $f_{a} (x) = (x - a)^{2}$ ist die um $a$ in Richtung der positiven $x -$ Achse verschobene Normalparabel mit dem Scheitelpunkt $S_{a} (a ∣ 0)$ .
  Ersetzt man in der Funktion $h$ die unabhängige Variable $x$ durch $x - 12$ , so erhält man $\displaystyle h_{12}(x)=\frac{5}{(x-12)^2+4}$ .
  Der Graph $G_{h_{12}}$ ergibt sich aus dem Graphen $G_{h}$ durch Verschiebung um $12 \thinspace LE$ in Richtung der positiven $x -$ Achse.
  Multipliziert man $h_{1} (x)$ mit dem Faktor $8$ , so werden alle Funktionswerte um den Faktor $8$ vergrößert. Man erhält den Graphen $G_{p}$
  $8\cdot h_1(x)=8\cdot \frac{5}{(x-12)^2+4}=\frac{40}{(x-12)^2+4}=p(x)$
  Der Graph $G_{h}$ ist achsensymmetrisch bzgl. der $y -$ Achse, weil sowohl Zählerterm als auch Nennerterm von $h$ gerade sind.
  Es gilt: $h(x)=h(-x)\thinspace \forall x\in \mathbb{R}.$
  Also ist der Graph $G_{h}$ symmetrisch zur Geraden mit der Gleichung $x = 0$ .
  Weil man $x$ durch $x - 12$ ersetzt hat, ist der Graph $G_{p}$ symmetrisch zur Geraden mit der Gleichung $x = 12.$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Eine auf einem Hausdach installierte Photovoltaikanlage wandelt Lichtenergie in elektrische Energie um. Für $4 \leq x \leq20$ beschreibt die Funktion p modellhaft die zeitliche Entwicklung der Leistung der Anlage an einem bestimmten Tag. Dabei ist $x$ die seit Mitternacht vergangene Zeit in Stunden und $p (x)$ die Leistung in kW (Kilowatt).
  Bestimmen Sie rechnerisch die Uhrzeit am Nachmittag auf Minuten genau, ab der die Leistung der Anlage weniger als $40$ % ihres Tageshöchstwerts von $10$ kW beträgt. (4P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ungleichungen lösen
  Die Leistung der PV-Anlage wird modellhaft durch die Funktion $p^{}$ beschrieben.
  $p(x)=\dfrac{40}{(x-12)^2+4}$
  Für welches $x$ gilt: $p (x) < 4$
  $\dfrac{40}{(x-12)^2+4}<4\iff \dfrac{10}{(x-12)^2+4}<1\iff 10<(x-12)^2+4\\\iff 6<(x-12)^2\iff \sqrt{6}<|x-12|$
  Diese Ungleichung bedeutet, welche Werte von $x$ haben von $12$ einen Abstand, der größer als $\sqrt{6}$ ist?
  Da in der Aufgabe nach einer Uhrzeit am Nachmittag gefragt ist, gilt:
  $\sqrt{6}<x-12\iff x > 12+\sqrt{6}\iff x > 12+2{,}449\\\Rightarrow x>14 \thinspace$ Uhr $27 \thinspace$ Minuten
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Die Funktion $p$ besitzt im Intervall $[4; 12]$ eine Wendestelle. Geben Sie die Bedeutung dieser Wendestelle im Sachzusammenhang an. (2P)
  
  Die Funktion $p$ ist im Intervall $\left[4;12\right]$ monoton steigend, denn
  $\displaystyle p'(x)=40\cdot\frac{-2\cdot(x-12)}{[(x-12)^2+4)]^2}=-80\cdot\frac{x-12}{[(x-12)^2+4]^2}>0$ .
  Da der Nennerterm von $p^{'} (x)$ als Quadrat positiv ist und der Zählerterm $-80\cdot (x-12)$ im Intervall $[4; 12]$ auch positiv ist, wächst $p$ im Intervall $[4; 12]$ .
  Der Wendepunkt ist ein (möglicher) Extrempunkt der 1. Ableitung, also der Veränderung (hier: Ansteigen) der Leistung.
  Bis zur Wendestelle $x_{w}$ wird das Ansteigen der Leistung immer stärker und nach der Wendestelle wird das Ansteigen schwächer. An der Wendestelle hat das Ansteigen der Leistung seinen Maximalwert erreicht. Um $12\thinspace$ Uhr hat das Ansteigen den Wert Null.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Die von der Anlage produzierte elektrische Energie wird vollständig in das Stromnetz eingespeist. Der Hauseigentümer erhält für die eingespeiste elektrische Energie eine Vergütung von $10$ Cent pro Kilowattstunde (kWh). Die in $[4; 20]$ definierte Funktion $x\mapsto E(x)$ gibt die elektrische Energie in kWh an, die die Anlage am betrachteten Tag von $4 : 00$ Uhr bis $x$ Stunden nach Mitternacht in das Stromnetz einspeist.
  Es gilt $E^{'} (x) = p (x)$ für $x \in[4;20]$ .
  Bestimmen Sie mithilfe der Abbildung einen Näherungswert für die Vergütung, die der Hauseigentümer für die von $10 : 00$ Uhr bis $14 : 00$ Uhr in das Stromnetz eingespeiste elektrische Energie erhält. (3P)
  
  Die in $\left[4{,}20\right]$ definierte Funktion $x\to E\left(x\right)$ gibt die eingespeiste elektrische Energie an und es gilt $E'\left(x\right)=p\left(x\right).$ Somit ist $E$ Stammfunktion von $p .$
  Und mittels $\int_{10}^{14}p(x)dx$ berechnet sich die eingespeiste Energie von $10 : 00$ Uhr bis $14 : 00$ Uhr.
  $\int_{10}^{14}p(x)dx$ lässt sich näherungsweise über den Inhalt der dem Graph von $p (x)$ einbeschriebenen Treppenfigur $U$ bzw. umbeschriebenen Treppenfigur $O$ berechnen.
  Da der Graph von $p (x)$ symmetrisch bzgl. der $y -$ Achse ist, genügt es, den Inhalt der Treppenfiguren im Intervall $[10; 12]$ zu berechnen. Den dann berechneten Wert des Flächeninhaltes multipliziert man mit $2.$
  Man unterteilt das Intervall $[10,12]$ in zwei Teilintervalle der Länge $\Delta x=1$ .
  Es gilt: $p(10)=\frac{40}{(10-12)^2+4}=5;\quad \quad \thinspace p(11)=\frac{40}{(11-12)^2+4}=8; \quad \quad \thinspace p(12)=10$
  Dann erhält man für die Fläche der einbeschriebenen Treppenfigur
  $U=5\cdot 1+8\cdot 1=13\thinspace \text{FE}$
  Und für die Fläche der umbeschriebenen Treppenfigur:
  $O=8\cdot 1+10\cdot 1=18\thinspace \text{FE}$
  Bildet man den Mittelwert von $U$ und $O$ , so erhält man: $\frac{U+O}{2}=\frac{31}{2}\thinspace \text{FE}$
  Somit kann man den Wert des Flächeninhaltes unter dem Graph von $p (x)$ im Intervall $[10; 14]$ näherungsweise mit $31 \thinspace \text{FE}$ angeben.
  Damit werden in der Zeit von $10 : 00$ Uhr bis $14 : 00$ Uhr etwa $31\thinspace \text{kWh}$ eingespeist.
  Der Hauseigentümer erhält als Vergütung $3{,}10\thinspace$ Euro.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉