Aufgabe B1
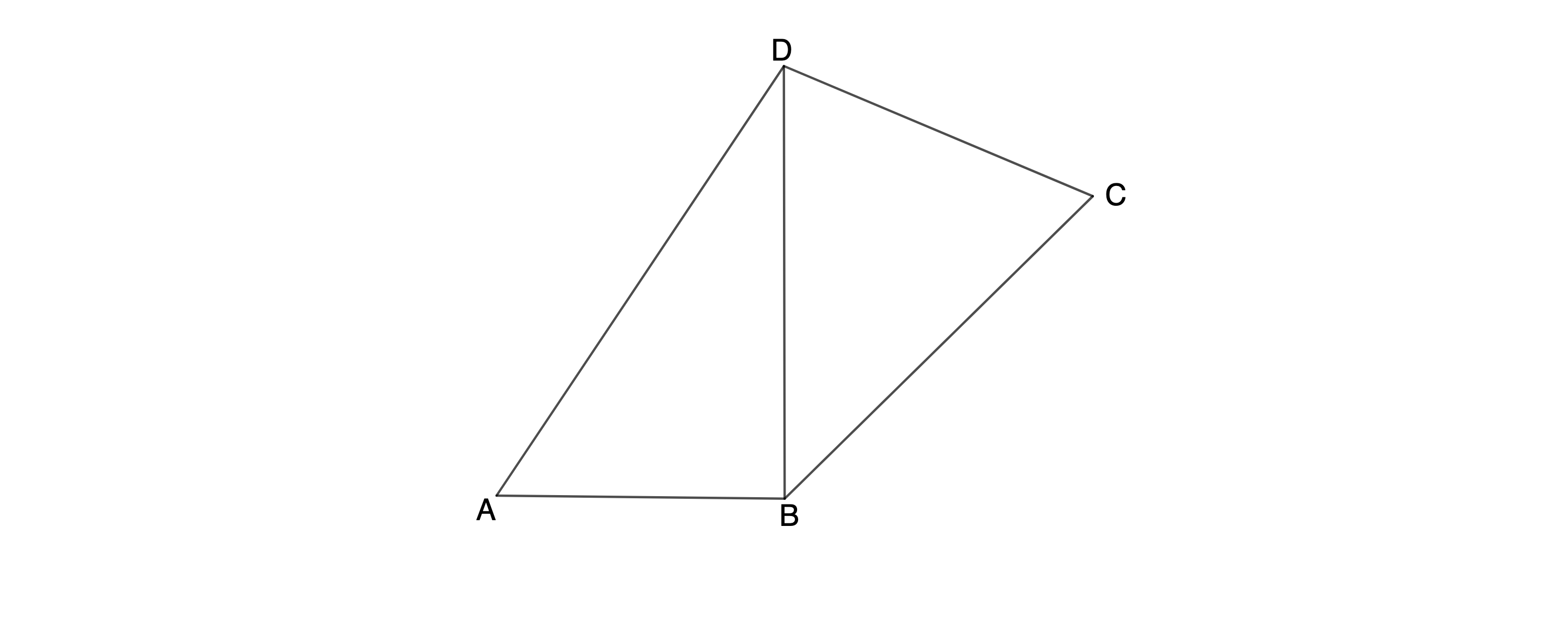
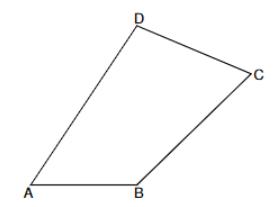
Die Skizze zeigt das Viereck .
Es gilt: ; ; ; .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
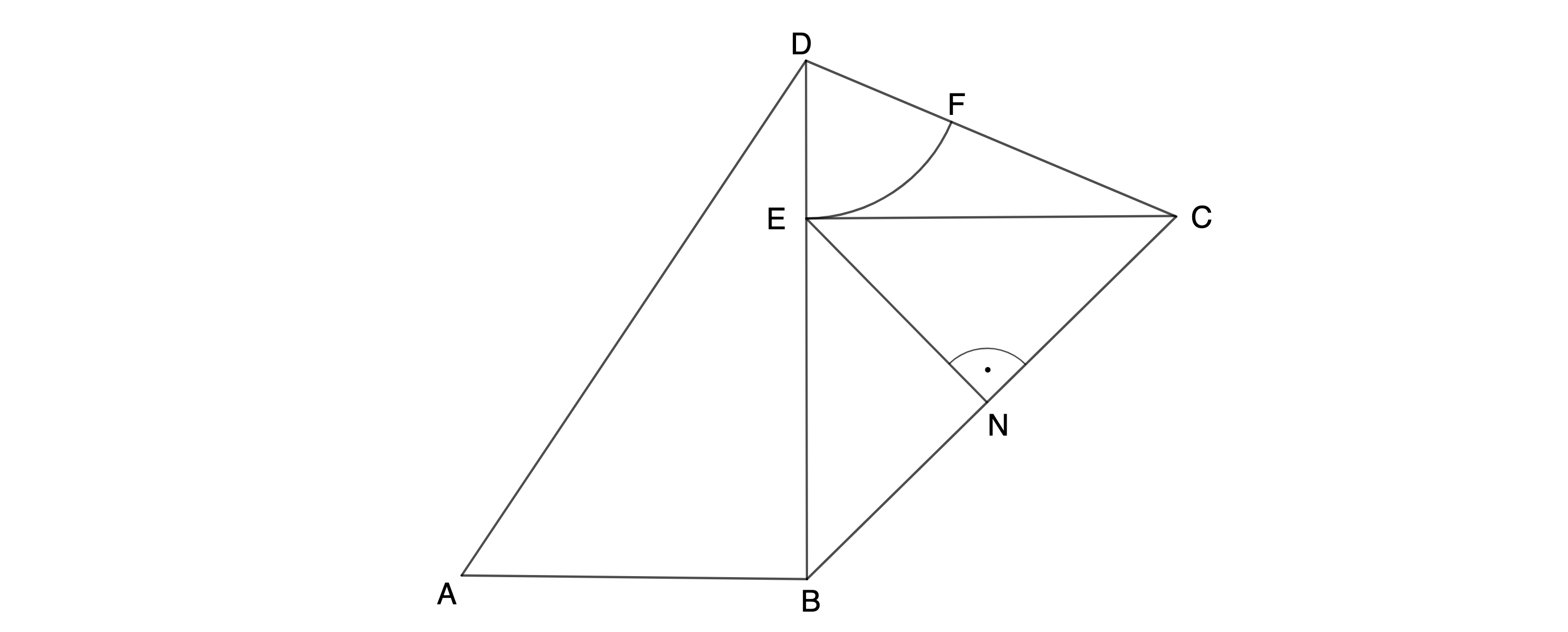
Zeichnen Sie das Viereck sowie die Strecke . Berechnen Sie sodann den Umfang des Vierecks . (4 P)
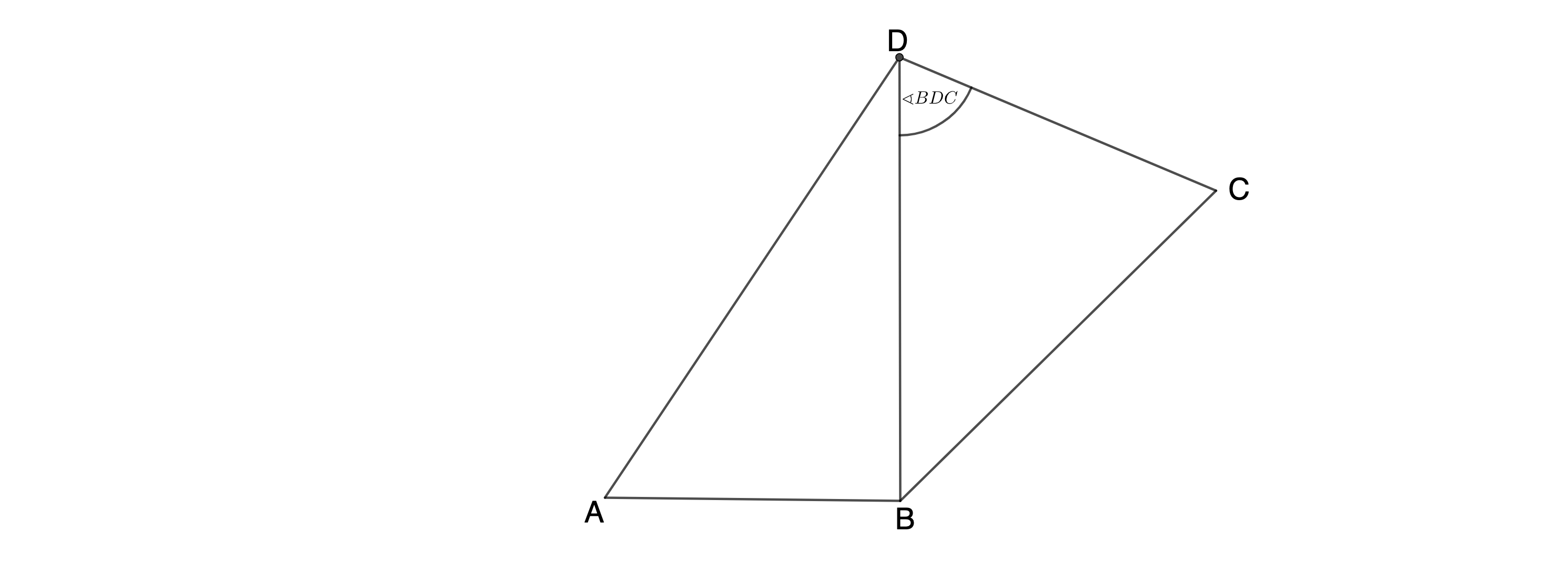
cmBerechnen Sie das Maß des Winkels . (2 P)
Ergebnis:
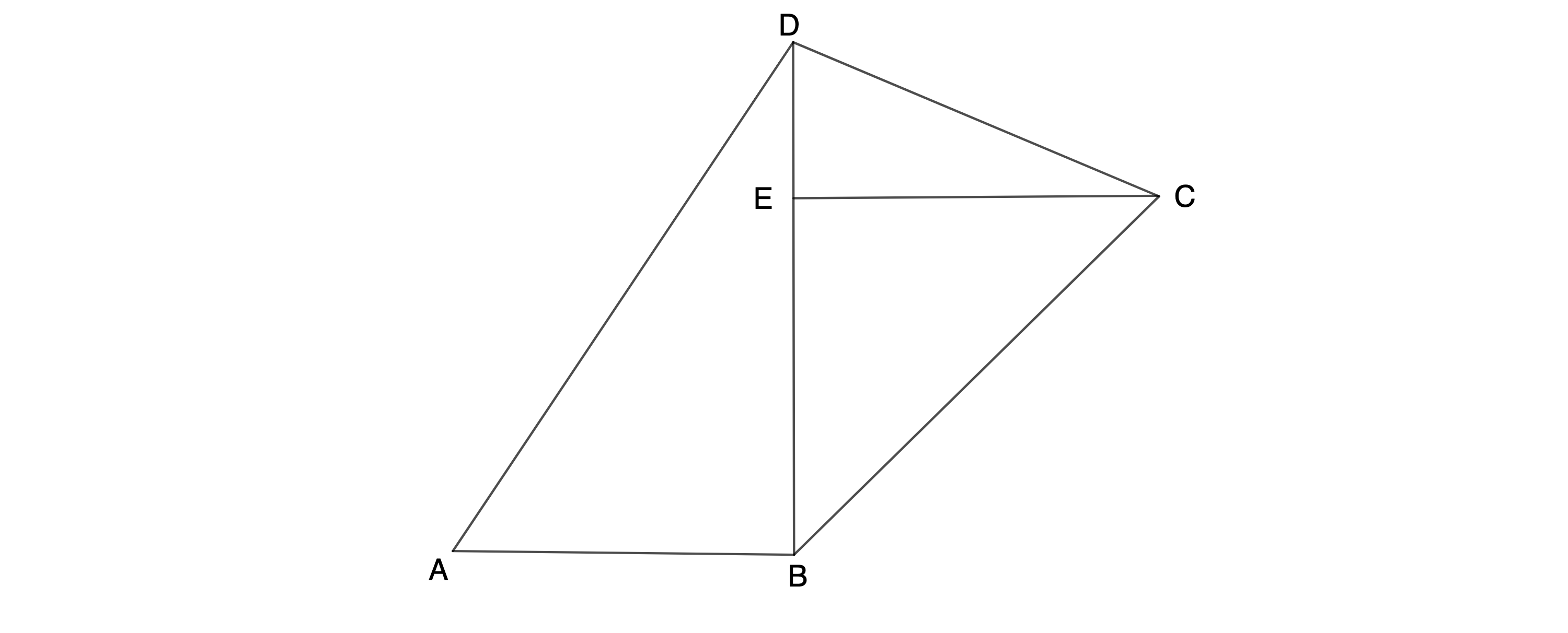
Die Strecke mit ist senkrecht zur Strecke . Ergänzen Sie die Zeichnung zu 1a) um die Strecke . Bestimmen Sie sodann rechnerisch die Längen der Strecken und . (3 P)
Teilergebnisse: ;
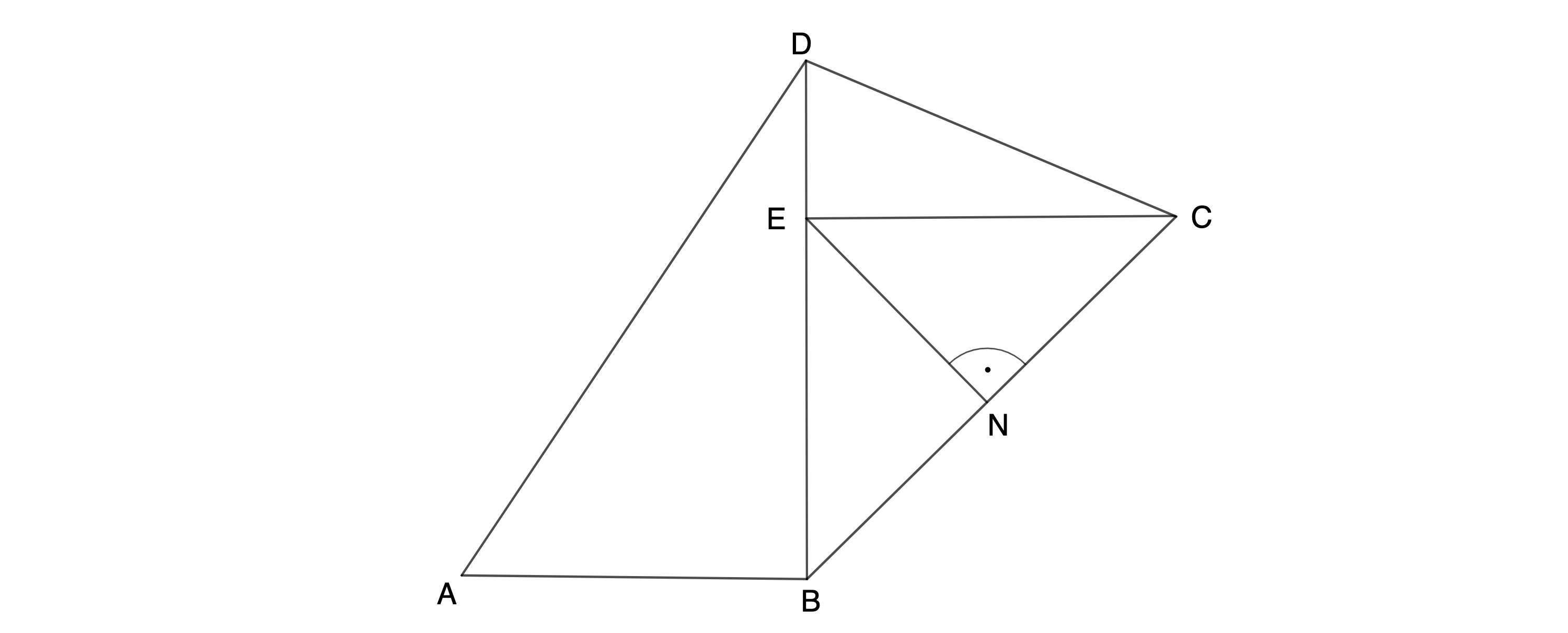
Die Strecke ist die kürzeste Verbindung des Punktes zur Strecke . Zeichnen Sie die Strecke in die Zeichnung zu 1a) ein und berechnen Sie deren Länge. (4 P)
cmDer Kreis mit dem Mittelpunkt und dem Radius schneidet die Strecke im Punkt .
Ergänzen Sie in der Zeichnung zu 1a) den zugehörigen Kreisbogen . Berechnen Sie sodann den Flächeninhalt der Figur , die durch die Strecken , , und den Kreisbogen begrenzt wird. (3 P)