In diesem Beispiel lernst du die ersten wichtigen Begriffe zum Thema kennen.
In einer Pralinenschachtel befinden sich 20 Pralinen.
12 Pralinen haben einen braunen Schokoladenüberzug, 8 einen aus weißer Schokolade.

Auf der Rückseite der Packung steht, dass 11 Pralinen eine Nougatfüllung haben, 8 der braunen Pralinen und 3 der Pralinen mit weißer Schokolade.
Tom darf ohne hinzusehen eine Praline nehmen.
Dann kannst du diese Fragen stellen:
a) Wie groß ist die Wahrscheinlichkeit, dass er eine mit braunem Überzug zieht?
Diese Wahrscheinlichkeit dieses Laplace-Experiments berechnest du als
b) Wie groß ist die Wahrscheinlichkeit, dass er eine mit Nougatfüllung zieht? Die Rechnung ist
c) Tom nimmt eine Praline und sieht, dass sie weiß ist. Wie groß ist die Wahrscheinlichkeit, dass er eine Praline mit Nougatfüllung hat?
Diesmal ist die Wahrscheinlichkeit
Erklärung: Die Wahrscheinlichkeit von ist eine andere als die
Wahrscheinlichkeit .
Bei der Berechnung von weiß Tom nichts über die Praline, die er zieht.
Bei der Berechnung von weiß Tom schon, dass er eine mit weißer Schokolade gezogen hat.
Es ist bereits eine „Bedingung“ (weiße Praline) bekannt.
Definition: ist die Wahrscheinlichkeit, dass eintritt, wenn bereits bekannt ist, dass eingetreten ist.
Eine andere Schreibweise ist auch .
In unserem Beispiel ist die Wahrscheinlichkeit, dass eine Praline mit Nougat gezogen wurde, wenn ich bereits weiß, dass sie weiß ist.
Man kann sich den Unterschied auch an einem Baumdiagramm deutlich machen:
mit der zweiten Pfadregel kann man berechen:
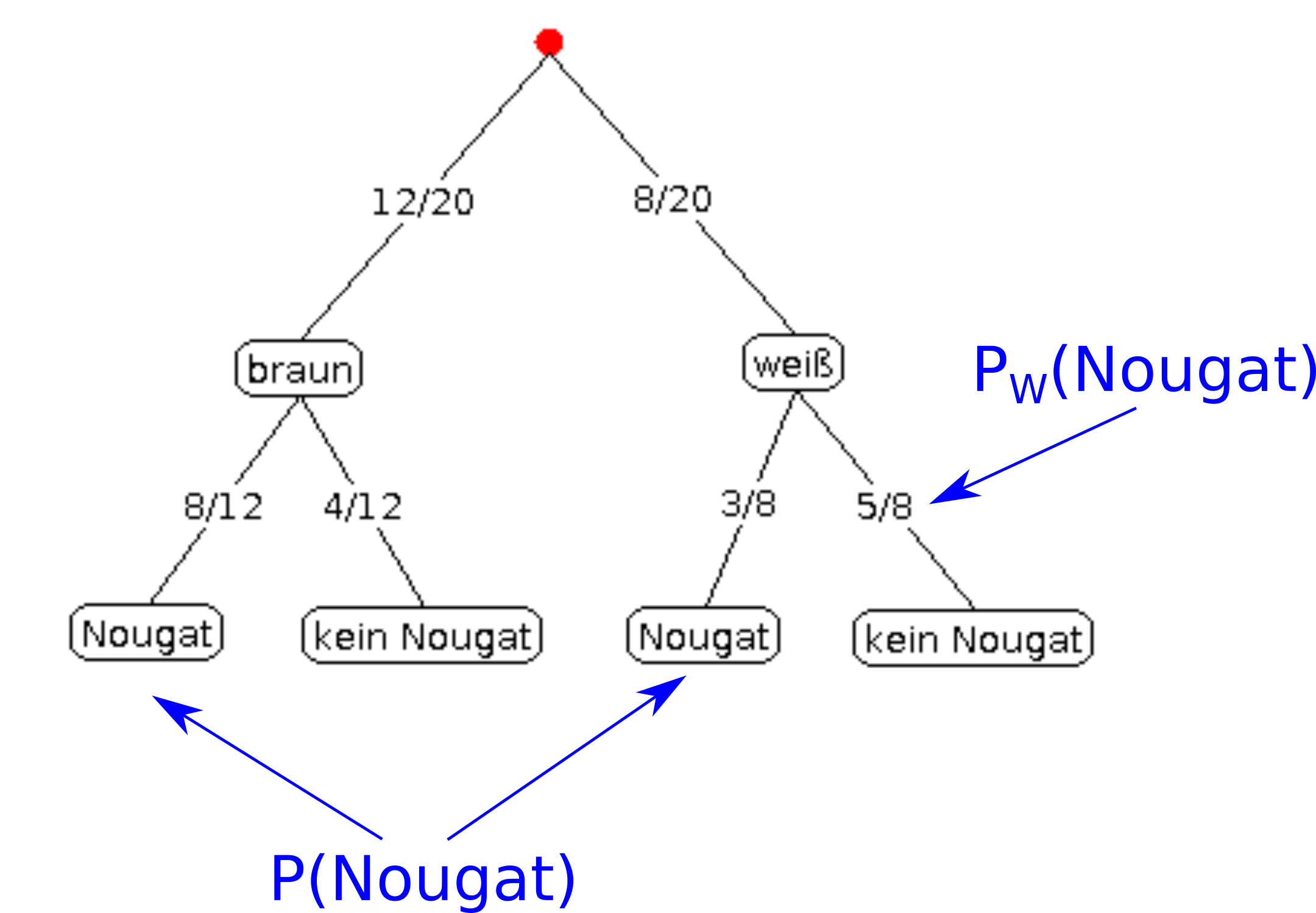
Die Wahrscheinlichkeit kann man direkt im Baumdiagramm ablesen:
Quellen
- openclipart.org
