1 Übersicht
Inhalt des Kurses
In diesem Kurs lernst du, wie man Brüche dividiert - mit ganzen Zahlen oder mit anderen Brüchen.
Vorkenntnisse
Du solltest wissen, wie man Brüche multipliziert.
Kursdauer
Dieser Kurs dauert etwa 30-40 Minuten.
2 Einschub: der Kehrbruch
Bei der Division von Brüchen benötigt man oft den sogenannten Kehrbruch. Diesen bestimmt man, indem man Zähler und Nenner miteinander vertauscht.
Beispiel:
Der Kehrbruch von ist .
Eine Besonderheit des Kehrbruchs ist, dass er bei Multiplikation mit dem ursprünglichen Bruch ergibt.
Im obigen Beispiel wäre also
Für den Kehrbruch gilt:
Je größer eine Zahl, desto kleiner ist ihr Kehrbruch
Je kleiner eine Zahl, desto größer ist ihr Kehrbruch
Bestimme den Kehrbruch.
Laden
Wie bestimmt man aber den Kehrbruch einer natürlichen Zahl?
Betrachte z.B. die Zahl 3. Diese kann man in den Bruch umwandeln.
Vertauscht man anschließend Zähler und Nenner, so erhält man als den Kehrbruch.
Bestimme den Kehrbruch.
Laden
3 Bruch geteilt durch ganze Zahl
Tim, Tom und Anna teilen sich Liter Orangensaft. Jeder trinkt gleich viel.
Wieviel Saft bekommt Anna?

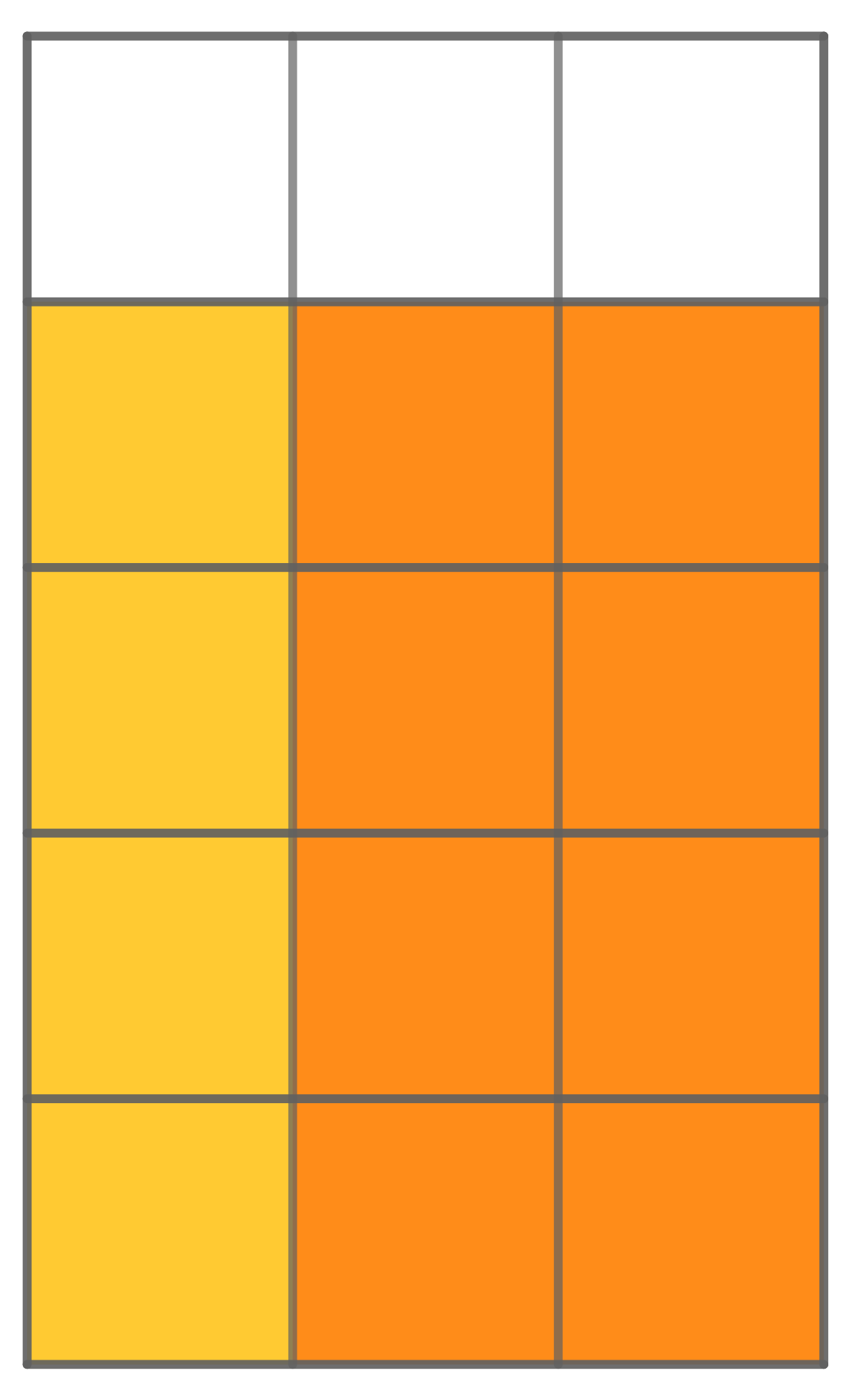
Liter Orangensaft können durch folgendes Rechteck veranschaulicht werden, dass aus vier orangen und einem weißen Teil besteht.

Wir teilen jedes der 5 kleineren Rechtecke in 3 gleichgroße Teile und sehen, dass offensichtlich gilt
Anna bekommt also Liter Orangensaft.
Vielleicht erinnert dich das an die Bonbon-Aufgabe (Link einfügen).
Durch 3 teilen () bedeutet also, dass man den "dritten Teil" von nimmt - das entspricht einer Multiplikation mit dem Kehrbruch . Wir können also rechnen:
4 Ganze Zahl geteilt durch Bruch
Jan will einen Pizzaabend veranstalten und Gäste einladen. Sein Taschengeld reicht aber nur für 3 Pizzen.
Er überlegt:"Jeder meiner Freunde isst ungefähr der Pizza, um satt zu werden".
Wie viele Freunde kann er also zu seiner Feier einladen?
Du musst also die Zahl suchen, die mit multipliziert ergibt.
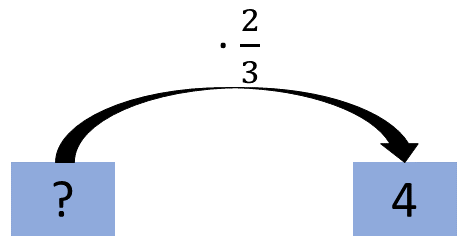
Die gesuchte Zahl ist also 6.
Sie löst auch die Gleichung
Doch wie kommt man am schnellsten auf dieses Ergebnis?
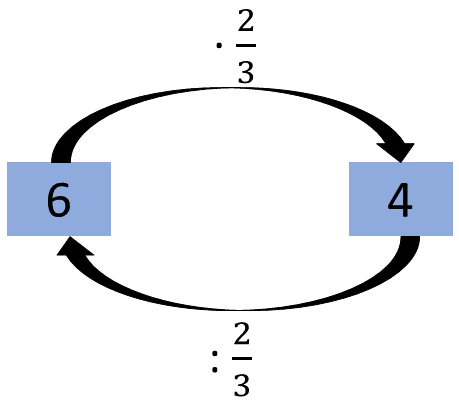
Ganz ähnlich zur vorherigen Teilaufgabe kann man auch hier statt durch zu teilen mit dem Kehrbruch multiplizieren:
| ↓ Multipliziere mit dem Kehrbruch | ||
| ↓ Schreibe auf einen Bruchstrich. | ||
| ↓ Multipliziere aus. | ||
| ↓ Kürze mit 2. | ||
5 Bruch geteilt durch Bruch
Die Pizzen kommen pünktlich und wurden vom Lieferanten bereits geachtelt.
Jan hat sich aber bei seiner Pizza-Bestellung verschätzt und es blieben Pizzen übrig.
Wie viele Stücken entspricht das?
Auch hier kannst du, ähnlich zur vorherigen Aufgabe rechnen:
| ↓ Multiplizieren mit dem Kehrbruch | ||
| ↓ Schreibe auf einen Bruchstrich | ||
| ↓ Multipliziere aus. | ||
| ↓ Kürze mit 2. | ||
Es sind also insgesamt 12 Stücke. Das lässt sich auch mit der Probe überprüfen:
| ↓ Schreibe auf einen Bruchstrich. | ||
| ↓ Kürze mit 4. | ||
| ↓ Schreibe als unechten Bruch. | ||
Du siehst also: auch bei der Division eines Bruches durch einen anderen Bruch funktioniert die Vorgehensweise.
Ein Bruch wird durch einen anderen dividiert, indem man den ersten Bruch mit dem Kehrbruch des zweiten Bruches multipliziert:
Hierbei stehen für beliebige ganze Zahlen.
Hilfe bietet dir auch folgender Merkspruch:
