Aufgaben zum Tetraeder

Wie gut kennst du dich aus? Mit diesen Übungsaufgaben lernst du das Berechnen von Größen im Tetraeder.

Berechnen verschiedener Größen eines Tetraeders

Berechne jeweils die Höhe, die Oberfläche und das Volumen der Tetraeder mit den gegebenen Seitenlängen $a$ . Runde das Ergebnis ggf. auf zwei Nachkommastellen.

$a=22~\text{m}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tetraeder

Höhe

Beschreibung	Berechnung
Verwende die Formel zur Berechnung der Höhe.	$h=\dfrac{a}{3}\cdot\sqrt{6}$
Setze den Wert für $a$ ein.	$h=\dfrac{22}{3}\cdot\sqrt{6}$
Berechne das Ergebnis. $\\$ Achte bei der Angabe des Ergebnisses auf die Einheit, in diesem Fall wird ein Längenmaß verwendet.	$h\approx 17{,}96~\text{m}$

Oberfläche

Beschreibung	Berechnung
Verwende die Formel zur Berechnung der Oberfläche.	$O=a^2\cdot\sqrt{3}$
Setze den Wert für $a$ ein.	$O=22^2\cdot\sqrt{3}$
Berechne das Ergebnis. $\\$ Achte bei der Angabe des Ergebnisses auf die Einheit, in diesem Fall wird ein Flächenmaß verwendet.	$O\approx 838{,}31~\text{m}^2$

Volumen

Beschreibung	Berechnung
Verwende die Formel zur Berechnung des Volumens.	$V=\dfrac{a^3}{12}\cdot\sqrt{2}$
Setze den Wert für $a$ ein.	$V=\dfrac{22^3}{12}\cdot\sqrt{2}$
Berechne das Ergebnis. $\\$ Achte bei der Angabe des Ergebnisses auf die Einheit, in diesem Fall wird ein Volumenmaß verwendet.	$V\approx 1254{,}88~\text{m}^3$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$a=12~\text{cm}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tetraeder

Höhe

Beschreibung	Berechnung
Verwende die Formel zur Berechnung der Höhe.	$h=\dfrac{a}{3}\cdot\sqrt{6}$
Setze den Wert für $a$ ein.	$h=\dfrac{12}{3}\cdot\sqrt{6}$
Berechne das Ergebnis. $\\$ Achte bei der Angabe des Ergebnisses auf die Einheit, in diesem Fall wird ein Längenmaß verwendet.	$h\approx 9{,}80~\text{cm}$

Oberfläche

Beschreibung	Berechnung
Verwende die Formel zur Berechnung der Oberfläche.	$O=a^2\cdot\sqrt{3}$
Setze den Wert für $a$ ein.	$O=12^2\cdot\sqrt{3}$
Berechne das Ergebnis. $\\$ Achte bei der Angabe des Ergebnisses auf die Einheit, in diesem Fall wird ein Flächenmaß verwendet.	$O\approx 249{,}42~\text{cm}^2$

Volumen

Beschreibung	Berechnung
Verwende die Formel zur Berechnung des Volumens.	$V=\dfrac{a^3}{12}\cdot\sqrt{2}$
Setze den Wert für $a$ ein.	$V=\dfrac{12^3}{12}\cdot\sqrt{2}$
Berechne das Ergebnis. $\\$ Achte bei der Angabe des Ergebnisses auf die Einheit, in diesem Fall wird ein Volumenmaß verwendet.	$V\approx 203{,}65~\text{cm}^3$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$a=5~\text{dm}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tetraeder

Höhe

Beschreibung	Berechnung
Verwende die Formel zur Berechnung der Höhe.	$h=\dfrac{a}{3}\cdot\sqrt{6}$
Setze den Wert für $a$ ein.	$h=\dfrac{5}{3}\cdot\sqrt{6}$
Berechne das Ergebnis. $\\$ Achte bei der Angabe des Ergebnisses auf die Einheit, in diesem Fall wird ein Längenmaß verwendet.	$h\approx 4{,}08~\text{dm}$

Oberfläche

Beschreibung	Berechnung
Verwende die Formel zur Berechnung der Oberfläche.	$O=a^2\cdot\sqrt{3}$
Setze den Wert für $a$ ein.	$O=5^2\cdot\sqrt{3}$
Berechne das Ergebnis. $\\$ Achte bei der Angabe des Ergebnisses auf die Einheit, in diesem Fall wird ein Flächenmaß verwendet.	$O\approx 43{,}30~\text{dm}^2$

Volumen

Beschreibung	Berechnung
Verwende die Formel zur Berechnung des Volumens.	$V=\dfrac{a^3}{12}\cdot\sqrt{2}$
Setze den Wert für $a$ ein.	$V=\dfrac{5^3}{12}\cdot\sqrt{2}$
Berechne das Ergebnis. $\\$ Achte bei der Angabe des Ergebnisses auf die Einheit, in diesem Fall wird ein Volumenmaß verwendet. In diesem Fall kann sogar die Einheit Liter $l$ verwendet werden.	$V\approx 14{,}73~\text{dm}^3$ $\\$ $V\approx 14{,}73~\text{l}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Berechnen der Kantenlänge eines Tetraeders

Berechne die Kantenlänge $a$ der Tetraeder aus den Teilaufgaben mithilfe der gegebenen Information (Höhe, Oberfläche oder Volumen). Runde ggf. auf zwei Nachkommastellen.

$h=12~\text{cm}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichung

Beschreibung	Berechnung
Verwende die Formel für die Höhe eines Tetraeders.	$h=\dfrac{a}{3}\cdot \sqrt{6}$
Setze die gegebene Information ein.	$12=\dfrac{a}{3}\cdot \sqrt{6}$
Forme die Gleichung nach $a$ um.	$a=\dfrac{12\cdot 3}{\sqrt{6}}$
Berechne das Ergebnis. Beachte die richtige Angabe der Einheit und runde auf zwei Nachkommastellen.	$a\approx 14{,}70~\text{cm}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$h=0{,}4~\text{dm}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichung

Beschreibung	Berechnung
Verwende die Formel für die Höhe eines Tetraeders.	$h=\dfrac{a}{3}\cdot \sqrt{6}$
Setze die gegebene Information ein.	$0{,}4=\dfrac{a}{3}\cdot \sqrt{6}$
Forme die Gleichung nach $a$ um.	$a=\dfrac{0{,}4\cdot 3}{\sqrt{6}}$
Berechne das Ergebnis. Beachte die richtige Angabe der Einheit und runde auf zwei Nachkommastellen.	$a\approx 0{,}49~\text{dm}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$O=82{,}4~\text{m}^2$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichungen, Unterthema "Rein quadratische Gleichungen"

Beschreibung	Berechnung
Verwende die Formel für die Oberfläche eines Tetraeders.	$O=a^2\cdot \sqrt{3}$
Setze die gegebene Information ein.	$82{,}4=a^2\cdot \sqrt{3}$
Forme die Gleichung nach $a$ um.	$a=\sqrt{\dfrac{82{,}4}{\sqrt{3}}}$
Berechne das Ergebnis. Beachte die richtige Angabe der Einheit und runde auf zwei Nachkommastellen.	$a\approx 6{,}74~\text{m}$

Die Umformung der Gleichung nach $a$ ergibt sich Schritt für Schritt aus:

$\displaystyle O$	$=$	$\displaystyle a^2\cdot \sqrt{3}$	$\displaystyle :\sqrt{3}$
$\displaystyle \dfrac{O}{\sqrt{3}}$	$=$	$\displaystyle a^2$	$\displaystyle \sqrt{}$
	↓	Beidseitiges Ziehen der Quadratwurzel "entfernt" das Quadrat auf der rechten Seite.
$\displaystyle \sqrt{\dfrac{O}{\sqrt{3}}}$	$=$	$\displaystyle a$
	↓	Die Seiten können einfach vertauscht werden, sie sind ja beide schließlich gleich.
$\displaystyle a$	$=$	$\displaystyle \sqrt{\dfrac{O}{\sqrt{3}}}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$O=105{,}5~\text{mm}^2$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichungen, Unterthema "Rein quadratische Gleichungen"

Beschreibung	Berechnung
Verwende die Formel für die Oberfläche eines Tetraeders.	$O=a^2\cdot \sqrt{3}$
Setze die gegebene Information ein.	$105{,}5=a^2\cdot \sqrt{3}$
Forme die Gleichung nach $a$ um.	$a=\sqrt{\dfrac{105{,}5}{\sqrt{3}}}$
Berechne das Ergebnis. Beachte die richtige Angabe der Einheit und runde auf zwei Nachkommastellen.	$a\approx 7{,}80~\text{mm}$

Die Umformung der Gleichung nach $a$ ergibt sich Schritt für Schritt aus:

$\displaystyle O$	$=$	$\displaystyle a^2\cdot \sqrt{3}$	$\displaystyle :\sqrt{3}$
$\displaystyle \dfrac{O}{\sqrt{3}}$	$=$	$\displaystyle a^2$	$\displaystyle \sqrt{}$
	↓	Beidseitiges Ziehen der Quadratwurzel "entfernt" das Quadrat auf der rechten Seite.
$\displaystyle \sqrt{\dfrac{O}{\sqrt{3}}}$	$=$	$\displaystyle a$
	↓	Die Seiten können einfach vertauscht werden, sie sind ja beide schließlich gleich.
$\displaystyle a$	$=$	$\displaystyle \sqrt{\dfrac{O}{\sqrt{3}}}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$V=745{,}9~\text{m}^3$

Beschreibung	Berechnung
Verwende die Formel für das Volumen eines Tetraeders.	$V=\dfrac{a^3}{12}\cdot \sqrt{2}$
Setze die gegebene Information ein.	$745{,}9=\dfrac{a^3}{12}\cdot \sqrt{2}$
Forme die Gleichung nach $a$ um.	$a=\sqrt[3]{\dfrac{745{,}9\cdot 12}{\sqrt{2}}}$
Berechne das Ergebnis. Beachte die richtige Angabe der Einheit und runde auf zwei Nachkommastellen.	$a\approx 18{,}50~\text{m}$

Die Umformung der Gleichung nach $a$ ergibt sich Schritt für Schritt aus:

$\displaystyle V$	$=$	$\displaystyle \dfrac{a^3}{12}\cdot \sqrt{2}$	$\displaystyle :\sqrt{2}$
$\displaystyle \dfrac{V}{\sqrt{2}}$	$=$	$\displaystyle \dfrac{a^3}{12}$	$\displaystyle \cdot 12$
$\displaystyle \dfrac{V\cdot 12}{\sqrt{2}}$	$=$	$\displaystyle a^3$	$\displaystyle \sqrt[3]{}$
	↓	Beidseitiges Ziehen der dritten Wurzel "entfernt" das "hoch drei" auf der rechten Seite.
$\displaystyle \sqrt[3]{\dfrac{V\cdot 12}{\sqrt{2}}}$	$=$	$\displaystyle a$
	↓	Die Seiten können einfach vertauscht werden, sie sind ja beide schließlich gleich.
$\displaystyle a$	$=$	$\displaystyle \sqrt[3]{\dfrac{V\cdot 12}{\sqrt{2}}}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$V = 13,5 l$

Beachte, dass die Einheit $l$ dasselbe ist, wie $\text{dm}^3$ .

Beschreibung	Berechnung
Verwende die Formel für das Volumen eines Tetraeders.	$V=\dfrac{a^3}{12}\cdot \sqrt{2}$
Setze die gegebene Information ein.	$13{,}5=\dfrac{a^3}{12}\cdot \sqrt{2}$
Forme die Gleichung nach $a$ um.	$a=\sqrt[3]{\dfrac{13{,}5\cdot 12}{\sqrt{2}}}$
Berechne das Ergebnis. Beachte die richtige Angabe der Einheit und runde auf zwei Nachkommastellen.	$a\approx 4{,}86~\text{dm}$

Die Umformung der Gleichung nach $a$ ergibt sich Schritt für Schritt aus:

$\displaystyle V$	$=$	$\displaystyle \dfrac{a^3}{12}\cdot \sqrt{2}$	$\displaystyle :\sqrt{2}$
$\displaystyle \dfrac{V}{\sqrt{2}}$	$=$	$\displaystyle \dfrac{a^3}{12}$	$\displaystyle \cdot 12$
$\displaystyle \dfrac{V\cdot 12}{\sqrt{2}}$	$=$	$\displaystyle a^3$	$\displaystyle \sqrt[3]{}$
	↓	Beidseitiges Ziehen der dritten Wurzel "entfernt" das "hoch drei" auf der rechten Seite.
$\displaystyle \sqrt[3]{\dfrac{V\cdot 12}{\sqrt{2}}}$	$=$	$\displaystyle a$
	↓	Die Seiten können einfach vertauscht werden, sie sind ja beide schließlich gleich.
$\displaystyle a$	$=$	$\displaystyle \sqrt[3]{\dfrac{V\cdot 12}{\sqrt{2}}}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

3
Volumen und Oberfläche eines Tetraeders
In der GeoGebra Anwendung befindet sich ein Tetraeder, der vergrößert bzw. verkleinert werden kann, indem man den Punkt A bewegt. Untersuche, wie sich die Oberfläche und das Volumen in Abhängigkeit der Seitenlänge $a$ verändert.
Für welche Seitenlänge ist das Volumen kleiner als die Oberfläche?
Für welche Seitenlänge ist das Volumen größer als die Oberfläche?
Für welche Seitenlänge (ungefähr) ist das Volumen gleich groß wie die Oberfläche?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tetraeder
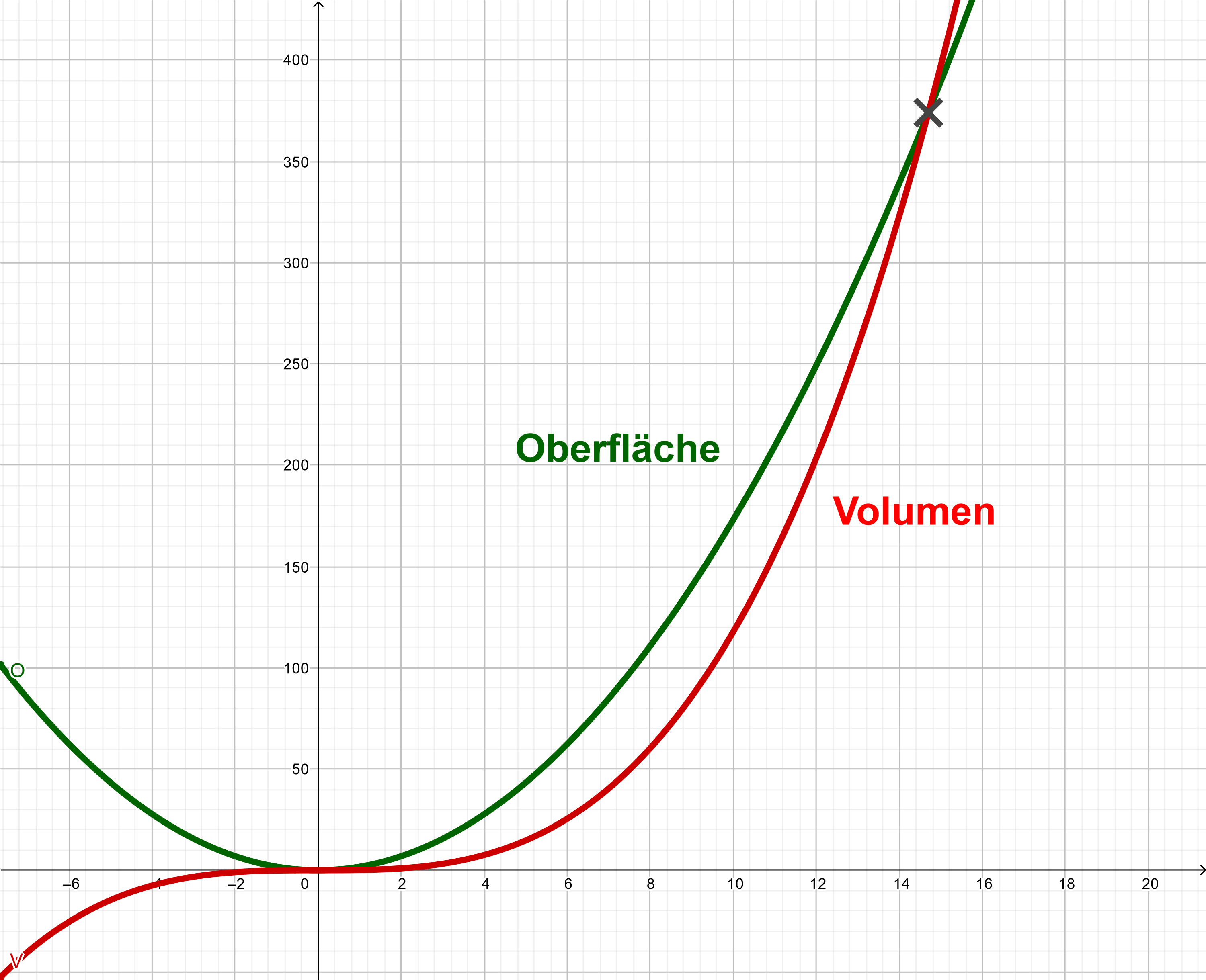
Für den Wert $a\approx14{,}7$ sind Oberfläche und Volumen etwa gleich. Ist die Seitenlänge kleiner, ist die Oberfläche größer als das Volumen. Ist die Seitenlänge größer, ist das Volumen größer als die Oberfläche.
Wieso der Wert $a\approx14{,}7$ ?
Volumen und Oberfläche sind gegeben durch die Formeln:
$V=\dfrac{a^3}{12}\cdot \sqrt{2}$
$O=a^2\cdot \sqrt{3}$
Sie können als Funktionen, in Abhängigkeit der Seitenlänge, betrachtet werden. Der Schnittpunkt deren Schaubilder zeigt genau diejenige Seitenlänge, für die die Funktionen den gleichen Wert annehmen.
Rechnerisch ergibt sich der genaue Wert für die Seitenlänge zu $a=\sqrt{216}$ .
Stelle verschieden große Seitenlängen ein und untersuche. Für die letzte Frage, suche im Bereich $15\le a\le20$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zum Tetraeder

Berechnen verschiedener Größen eines Tetraeders

Höhe

Oberfläche

Volumen

Hast du eine Frage oder Feedback?

Höhe

Oberfläche

Volumen

Hast du eine Frage oder Feedback?

Höhe

Oberfläche

Volumen

Hast du eine Frage oder Feedback?

Berechnen der Kantenlänge eines Tetraeders

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Volumen und Oberfläche eines Tetraeders