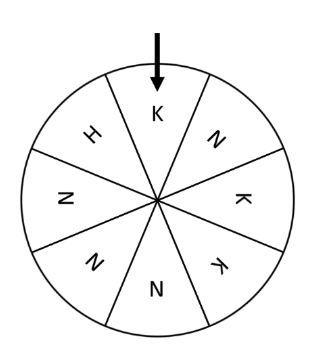
Bei einem Gewinnspiel wird nebenstehendes Glücksrad gedreht, bei dem die einzelnen Kreissektoren gleich groß sind.
Diesem Zufallsexperiment wird der Ergebnisraum zugrunde gelegt. Dabei steht H für den Hauptgewinn, K für einen Kleingewinn und N für eine Niete.
Vier Personen drehen jeweils einmal am Glücksrad.
Ermitteln Sie die Wahrscheinlichkeit dafür, dass keiner von ihnen eine Niete erzielt. (2 BE)
Für einen Einsatz von 2 € darf man einmal am Glücksrad drehen. Für einen Hauptgewinn erhält der Teilnehmer 7 € und für einen Kleingewinn 3 € ausbezahlt. Bei einer Niete verfällt der Einsatz.
Berechnen Sie den Erwartungswert für die Zufallsgröße X: „Auszahlung in Euro“ und interpretieren Sie das Ergebnis im Zusammenhang mit dem Einsatz. (3 BE)
