Teil 1 Stochastik

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellungen im Original zum Ausdrucken findest du hier.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die sechs Seiten eines Laplace-Würfels sind mit den Ziffern 1,2,3,4,5 und 6 beschriftet. Dieser Würfel wird zweimal hintereinander geworfen.
Betrachtet wird folgendes Ereignis E.
E: "Die Summe der beiden gewürfelten Augenzahlen ist höchstens drei."
Geben Sie E in aufzählender Mengenschreibweise an und ermitteln Sie die zugehörige Wahrscheinlichkeit für dieses Ereignis. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ereignis
Ereignis in aufzählender Mengenschreibweise
Elemente der Ergebnismenge $\Omega$ sind Tupel der Form $\left(w_1,w_2\right)$ , wobei $w_1,w_{2\ }\in\left\{1;2;3;4;5;6\right\}$ die jeweilige Augenzahl beim ersten Wurf bzw zweiten Wurf ist.
Die aufzählende Mengenschreibweise von E: "Augensumme höchstens drei" lautet also:
$E=\left\{\left(1;1\right),\left(1;2\right),\left(2;1\right)\right\}$
Wahrscheinlichkeit des Ereignisses
Da es sich um einen Laplace-Würfel handelt, sind alle Ergebnisse, also alle Augenzahlen, gleich wahrscheinlich. Somit ist also auch jedes Tupel bei zweimaligem Werfen gleich wahrscheinlich und das zweimalige Werfen ist ebenfalls ein Laplace-Experiment, bei dem jedes Ergebnis gleich wahrscheinlich ist.
Bei einem Laplace-Experiment kann die Wahrscheinlichkeit berechnet werden durch:
$P\left(E\right)=\dfrac{\text{günstige Ergebnisse}}{\text{mögliche Ergebnisse}}=\dfrac{|E|}{|\Omega|}$
Dabei beschreiben die senkrechten Striche die Mächtigkeit einer Menge, also die Anzahl ihrer Elemente.
Es ist $\left|E\right|=3$ , denn es sind drei Tupel in der Menge enthalten.
Für $\left|\Omega\right|$ muss man sich überlegen, wie viele mögliche Kombinationen es beim zweimaligen Würfeln gibt. Beim ersten Wurf gibt es 6 mögliche Ausgänge. Für jedes dieser Ergebnisse gibt es beim 2. Wurf 6 mögliche Elemente. Insgesamt also:
$\left|\Omega\right|=6\cdot6=36$ und somit $P\left(E\right)=\frac{3}{36}\approx8{,}33\%$

Für zwei gegebene Ereignisse A und B gilt: $P\left(\overline{A}\right)=\frac{2}{3},\ P\left(A\cap B\right)=0\$ und $P\left(A\cup B\right)=\frac{4}{9}$ .

Berechnen Sie die Wahrscheinlichkeit $P\left(B\right)$ , z.B. mithilfe einer Vierfeldertafel. (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel

Initiale Werte in die Vierfeldertafel eintragen

Übertrage die gegebenen Werte in die Vierfeldertafel, dabei kannst du $P\left(A\cup B\right)$ noch nicht direkt eintragen.

	$A$	$\overline{A}$
$B$	$0$
$\overline{B}$
		$\frac{2}{3}$	$1$

Berechne mithilfe der gegebenen Werte weitere Werte:

	$A$	$\overline{A}$
$B$	$0$
$\overline{B}$
	${\color{red}\frac 1 3}$	$\frac{2}{3}$	$1$

	$A$	$\overline{A}$
$B$	$0$
$\overline{B}$	${\color{red}\frac 1 3}$
	$\frac 1 3$	$\frac{2}{3}$	$1$

Zusammengesetzte Wahrscheinlichkeit verwenden

Die zusammengesetzte Wahrscheinlichkeit $P\left(A\cup B\right)$ lässt sich wie folgt beschreiben:

$P\left(A\cup B\right)=P\left(A\cap B\right)+P\left(A\cap\overline{B}\right)+P\left(\overline{A}\cap B\right)$

Setze die gegeben Werte ein und löse die Gleichung:

$\displaystyle P\left(A\cup B\right)$	$=$	$\displaystyle P\left(A\cap B\right)+P\left(A\cap\overline{B}\right)+P\left(\overline{A}\cap B\right)$
	↓	Einsetzen
$\displaystyle \frac{4}{9}$	$=$	$\displaystyle 0+\frac 1 3 + P(\overline A \cap B)$	$\displaystyle -\frac{1}{3}$
$\displaystyle \frac{1}{9}$	$=$	$\displaystyle P\left(\overline{A}\ \cap B\right)$

Mit dieser Information lässt sich die Vierfeldertafel vervollständigen und $P (B)$ angeben:

	$A$	$\overline{A}$
$B$	$0$	$\frac{1}{9}$	${\color{red}\frac 1 9}$
$\overline{B}$	$\frac 1 3$	$\frac{5}{9}$	$\frac{8}{9}$
	$\frac 1 3$	$\frac{2}{3}$	$1$

$P\left(B\right)=\frac{1}{9}$

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Bei einem Gewinnspiel wird nebenstehendes Glücksrad gedreht, bei dem die einzelnen Kreissektoren gleich groß sind.
Diesem Zufallsexperiment wird der Ergebnisraum $\Omega=\left\{H;K;N\right\}$ zugrunde gelegt. Dabei steht H für den Hauptgewinn, K für einen Kleingewinn und N für eine Niete.
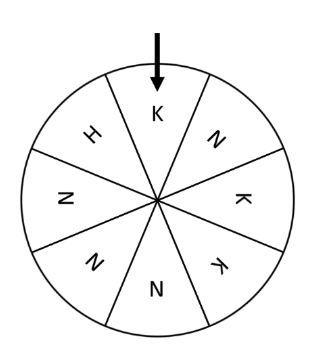
1. Vier Personen drehen jeweils einmal am Glücksrad.
  Ermitteln Sie die Wahrscheinlichkeit dafür, dass keiner von ihnen eine Niete erzielt. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kombinatorik
  Wahrscheinlichkeiten der Elementarereignisse
  Da jeder der acht Sektoren gleich groß ist, kann die Wahrscheinlichkeit der drei Ergebnisse $H, N$ und $K$ als Laplacewahrscheinlichkeit ausgedrückt werden:
  $P(\text{Sektor})=\frac{\text{Anzahl Sektoren mit diesem Buchstaben}}{\text{Anzahl aller Sektoren}}$
  also: $P(H)=\frac{1}{8},\ P\left(K\right)=\frac{3}{8},\ P\left(N\right)=\frac{4}{8}=\frac 1 2$
  Wahrscheinlichkeit für 4-mal keine Niete
  Da sich das Glücksrad nach dem Drehen nicht verändert, ist das Experiment vergleichbar zu einem Urnenexperiment "Ziehen mit Zurücklegen", da nacheinander gedreht wird, wird die Reihenfolge beachtet.
  Deshalb kann die Wahrscheinlichkeit berechnet werden durch
  $P\left(\text{"4 mal keine Niete"}\right)=p^4$ ,
  wobei $p$ die Wahrscheinlichkeit dafür ist, keine Niete zu bekommen und die $4$ von den vier Personen kommt.
  Die Wahrscheinlichkeit, keine Niete zu bekommen ist
  $P(\overline N)=1-P(N)=\frac 1 2$
  Also ist
  $P\left(\text{"4 mal keine Niete"}\right)=0{,}5^4=6{,}25\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Für einen Einsatz von 2 € darf man einmal am Glücksrad drehen. Für einen Hauptgewinn erhält der Teilnehmer 7 € und für einen Kleingewinn 3 € ausbezahlt. Bei einer Niete verfällt der Einsatz.
  Berechnen Sie den Erwartungswert für die Zufallsgröße X: „Auszahlung in Euro“ und interpretieren Sie das Ergebnis im Zusammenhang mit dem Einsatz. (3 BE)
  
  Die möglichen Auszahlungsbeträge sind 7 € (Hauptgewinn H), 3 € (Kleingewinn K) und 0 € (Niete N).
  Ein Blick auf das Glücksrad verrät dir, dass es 8 Sektoren gibt, davon 1 Sektor Hauptgewinn, 3 Sektoren Kleingewinn und 4 Sektoren Niete. Damit ergibt sich für die Wahrscheinlichkeiten:
  $P(H)=\frac 1 8, P(K)=\frac 38$ und $P(N)=\frac 4 8 =\frac 1 2$
  Bestimme den Erwartungswert, indem du jeden Auszahlungsbetrag mit seiner Wahrscheinlichkeit multiplizierst und die Produkte addierst:
  $E(X)=\frac 1 8\cdot 7 €+\frac 3 8 \cdot 3 € + \frac 1 2 \cdot 0 €= 2 €$
  Im Durchschnitt bekommt man pro Spiel 2 € ausbezahlt.
  Da der Einsatz genau so hoch ist wie der erwartete Auszahlungsbetrag, ist das Spiel fair.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Um den Erwartungswert zu bestimmen, brauchst du für jeden möglichen Auszahlungsbetrag die Wahrscheinlichkeit. Beachte, dass du den Einsatz dabei nicht berücksichtigen sollst.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Teil 1 Stochastik

Ereignis in aufzählender Mengenschreibweise

Wahrscheinlichkeit des Ereignisses

Initiale Werte in die Vierfeldertafel eintragen

Zusammengesetzte Wahrscheinlichkeit verwenden

Wahrscheinlichkeiten der Elementarereignisse

Wahrscheinlichkeit für 4-mal keine Niete

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?