1 Mitbewohner*in gesucht!
Emmy, Maryam, Carl und Bertrand wohnen zusammen in einer WG in der Weierstraße 2. Seit Kurt ausgezogen ist, suchen sie eine*n neue*n Mitbewohner*in für das freigewordene Zimmer. Nach ihrer Anzeige auf chillig-und-billig.de melden sich binnen kürzester Zeit viele Interessent*innen - so viele, dass Emmy, Maryam, Carl und Bertrand sich nach 17 Minuten und 73 Bewerbungen entscheiden, die Anzeige wieder von der Seite zu nehmen. Sie beschließen, mit den vorhandenen Bewerber*innen ein WG-Casting durchzuführen, um den*die optimale*n Mitbewohner*in zu bestimmen.
Alle sind sich einig, dass das hervorstechendste Merkmal eines guten Mitbewohners sein sollte, dass er oder sie gerne scharfes Essen isst - je schärfer, desto besser. Beim WG-Casting soll nun deshalb jede*r Bewerber*in unauffällig auf die Probe gestellt werden. Die schärferesistenteste Person soll das Zimmer bekommen.
Die Regeln von chillig-und-billig.de fordern, dass man einem*r Bewerber*in nach dem Casting sofort zu- oder absagen muss. Die Betreiber der Seite begründen das folgendermaßen: "Nach einem Casting lange auf eine Rückmeldung zu warten erschwert Bewerber*innen die Planung und damit die Wohnungssuche. Wer sich bewirbt und zu einem Casting geht, soll auch schnell eine Antwort bekommen. Denn Zeit ist nicht billig und Warten ist unchillig." Emmy, Maryam, Carl und Bertrand können also nicht erst alle 73 Bewerber*innen begutachten und danach eine Entscheidung treffen. Stattdessen müssen sie nach jedem Casting entscheiden, ob sie die Person nehmen oder nicht. Erst nach einer Absage bekommen sie die nächste Person zum Casting zugeteilt.
Um garantiert eine optimale Entscheidung zu treffen, müsste man die Zukunft voraussehen können. Aber es kann ja niemand wissen, ob nach einer bestimmten Person noch eine bessere kommt oder nicht. Deshalb müssen Emmy, Maryam, Carl und Bertrand probabilistisch vorgehen: Was wäre eine gute Casting-Strategie, um mit möglichst hoher Wahrscheinlichkeit den*die beste*n Kandidat*in zu wählen?

Abb. 1: Niemand kann die Zukunft voraussehen.
Quellen:
Abb. 1: Bild zukunft-kristallkugel-vorhersage von Rilsonav, Pixabay License, via Pixabay
2 Erste Casting-Strategien
Die vier diskutieren, wie sie am besten vorgehen sollten. Um die Ergebnisse für zukünftige WG-Castings nutzen zu können, stellen sie ihre Überlegungen für eine allgemeine Anzahl von Bewerber*innen an.
Bertrand hat eine Idee: "Lass doch einfach den ersten Bewerber nehmen. Erinnert ihr euch noch an diese Multiple-Choice Klausur letztes Semester? Da war auch die erste Option immer die richtige."
Die vier überlegen und kommen zu folgendem Ergebnis: Die Wahrscheinlichkeit, dass sich die schärferesistenteste Person ausgerechnet auf der ersten Position in der Liste der Bewerber*innen befindet, beträgt genau
Bei einer großen Zahl Bewerbungen ist es mit dieser Methode nicht besonders wahrscheinlich, die beste Person zu erwischen. Zum Beispiel würde die Erfolgswahrscheinlichkeit bei Bewerbungen nur betragen. Das ist nicht besonders viel.
Carl widerspricht dem Argument, dass die erste Option immer die beste sei: "Das war vielleicht in der Klausur so, aber bei Entscheidungen, wo es wirklich um was geht, soll man nie die erstbeste Option nehmen. Das weiß doch jeder! Lehnen wir doch den ersten Bewerber nach dem Casting einfach ab und nehmen den zweiten."
Es dauert nicht lang, bis die vier die Erfolgswahrscheinlichkeit der von Carl vorgeschlagenen Methode ermittelt haben: Die Wahrscheinlichkeit, dass sich die beste Person auf Platz 2 in der Liste der Bewerber*innen befindet, beträgt ebenfalls nur
Auch nach Emmys Vorschlag, "Die Antwort auf Alles ist 42. Was, wenn wir einfach immer den 42. nehmen?", müssen die vier feststellen, dass die Wahrscheinlichkeit, auf diese Weise den*die beste*n Bewerber*in zu wählen, genau dieselbe ist: .
"Ja nee", wirft Bertrand ein, "wenn wir jetzt schon ausmachen, nach dem*der wievielten Bewerber*in wir das Casting beenden, dann kriegen wir ja immer mit der gleichen Wahrscheinlichkeit den*die Beste*n. Dann können wir uns die Castings auch sparen und wirklich einfach den ersten nehmen!"
Maryam verliert die Geduld: "Ey Leute, ich glaub nicht, dass das zu was führt. Das muss doch noch besser gehen. Wir müssen mehr out of the box denken."
3 Die bessere Strategie
Maryam fährt fort: "Ich stimme Carl zu, dass wir nicht den*die erstbeste*n Bewerber*in nehmen sollten. Die Erfolgswahrscheinlichkeit ist viel zu gering. Aber wenn wir den*die erste*n Bewerber*in nach dem Casting ablehnen, will ich danach keinen nehmen, der*die schlechter als der*die Erste ist. Das wär ganz schön blöd."
"Ja stimmt", meint Carl. "Dann nehmen wir halt danach den*die Nächste*n, der*die besser ist als der*die Erste."
"Wenn wir so vorgehen, sollten wir aber erst einen besseren Eindruck haben, wie die Bewerber*innen überhaupt sind", gibt Emmy zu bedenken. "Ich bin dafür, dass wir anfangs noch mehr Leute ablehnen, bevor wir jemanden auswählen. Bewerbungen haben wir ja genug."
Alle finden diesen Vorschlag gut. Die vier beschließen, sich erst eine gewisse Anzahl an Bewerber*innen anzuschauen und abzulehnen. Danach interviewen sie den Rest und nehmen die nächste Person, die besser als die ersten Bewerber*innen ist.

Person r-1 war die beste unter den ersten r, die abgelehnt wurden. Danach ist Person r+4 die erste, die besser ist, und wird deshalb ausgewählt.
Nur Bertrand macht sich noch Sorgen: "Aber je mehr wir am Anfang ablehnen, desto größer ist doch die Wahrscheinlichkeit, dass sich die beste Person unter den bereits abgelehnten Personen befindet! Wie soll das funktionieren?"
"Wir müssen einfach nur klug wählen", meint Emmy. "Dann wird das schon passen."
"Dann sag doch mal, wie wir 'klug' wählen können", fordert Bertrand. Unter den erwartungsvollen Blicken der anderen sucht sich Emmy Papier und einen Bleistift und beginnt zu rechnen.
4 Mathematische Untersuchung der Strategie
Die Strategie der vier ist, die ersten der Bewerber*innen abzulehnen und danach die erste Person zu nehmen, die besser als die ersten Bewerber*innen ist. Emmy will nun so wählen, dass die Wahrscheinlichkeit , mit dieser Strategie die beste Person zu finden, maximal ist. Dafür muss sie in Abhängigkeit von berechnen.
Emmy geht die einzelnen Kandidat*innen nach den ersten Leuten durch und berechnet jeweils die Wahrscheinlichkeit, dass die Person die beste Wahl ist und sie mit der Strategie ausgewählt wird.
Was ist die Wahrscheinlichkeit, dass sie die beste Wahl ist und sie mit der Strategie ausgewählt wird?
Die Wahrscheinlichkeit, dass sie die beste Person ist, ist wieder .
Weil sie die beste Person ist, ist sie auch besser als die ersten Personen. Weil sie direkt nach den abgelehnten Personen kommt und besser als sie ist, wird sie auch ausgewählt. Also ist die Wahrscheinlichkeit, dass sie ausgewählt wird, .
Insgesamt ist die Wahrscheinlichkeit, dass die ste Person die beste ist und ausgewählt wird, gleich .
Wie sieht es mit der nächsten Bewerbung aus?
Was ist die Wahrscheinlichkeit, dass sie die beste Wahl ist und sie mit der Strategie ausgewählt wird?
Dass Person die beste ist, gilt mit einer Wahrscheinlichkeit von .
Wir wählen Person genau dann aus, wenn der*die Bewerber*in nicht besser war als die ersten Personen. Mit welcher Wahrscheinlichkeit ist Person besser als die ersten Bewerber*innen? Das ist der Fall, wenn die beste Person aus den Bewerber*innen Person ist. Das gilt mit einer Wahrscheinlichkeit von .
Unsere gesuchte Wahrscheinlichkeit ist also
Insgesamt ist die Wahrscheinlichkeit dafür, dass die te Person die beste ist und mit dieser Strategie ausgewählt wird, gleich .
Was gilt allgemeiner für die te Person, die nach den ersten kommt?
Was ist die Wahrscheinlichkeit, dass sie die beste Wahl ist und sie mit der Strategie ausgewählt wird?
Die Person ist die beste mit einer Wahrscheinlichkeit von .
Wir wählen sie genau dann aus, wenn die Personen nicht besser sind als die beste der ersten Personen. Mit welcher Wahrscheinlichkeit ist keine der Personen besser als die ersten Personen? Das gilt genau dann, wenn die beste der ersten Personen eine der Personen ist. Die Wahrscheinlichkeit dafür ist
Insgesamt ist die Wahrscheinlichkeit, dass die te Person die beste Wahl ist und mit der Strategie ausgewählt wird, gleich .
Die Gesamtwahrscheinlichkeit, mit der Strategie die beste Person auszuwählen, ist die Summe der einzelnen Wahrscheinlichkeiten für die einzelnen Personen:
Emmy präsentiert die Wahrscheinlichkeit stolz ihren Freunden.
Bertrand ist noch nicht zufrieden. "Wie sollen wir nun das richtige finden, für das maximal ist?", fragt er.
"Das ist ja einfach eine Extremwertaufgabe", meint Carl, "ich weiß, wie das geht, da muss man die Ableitung von finden und herausfinden, für welches die Ableitung Null ist!"
"Wie willst du denn bitte diese Funktion nach ableiten?!", entgegnet Maryam. "Siehst du nicht, dass auch der Index der Summe von abhängt?"
"Ich hab da eine Idee", meint Emmy. "Wir können die Summe durch ein Integral abschätzen."
"Die Summe ist dann die linke Riemannsumme des Integrals", erklärt Emmy.
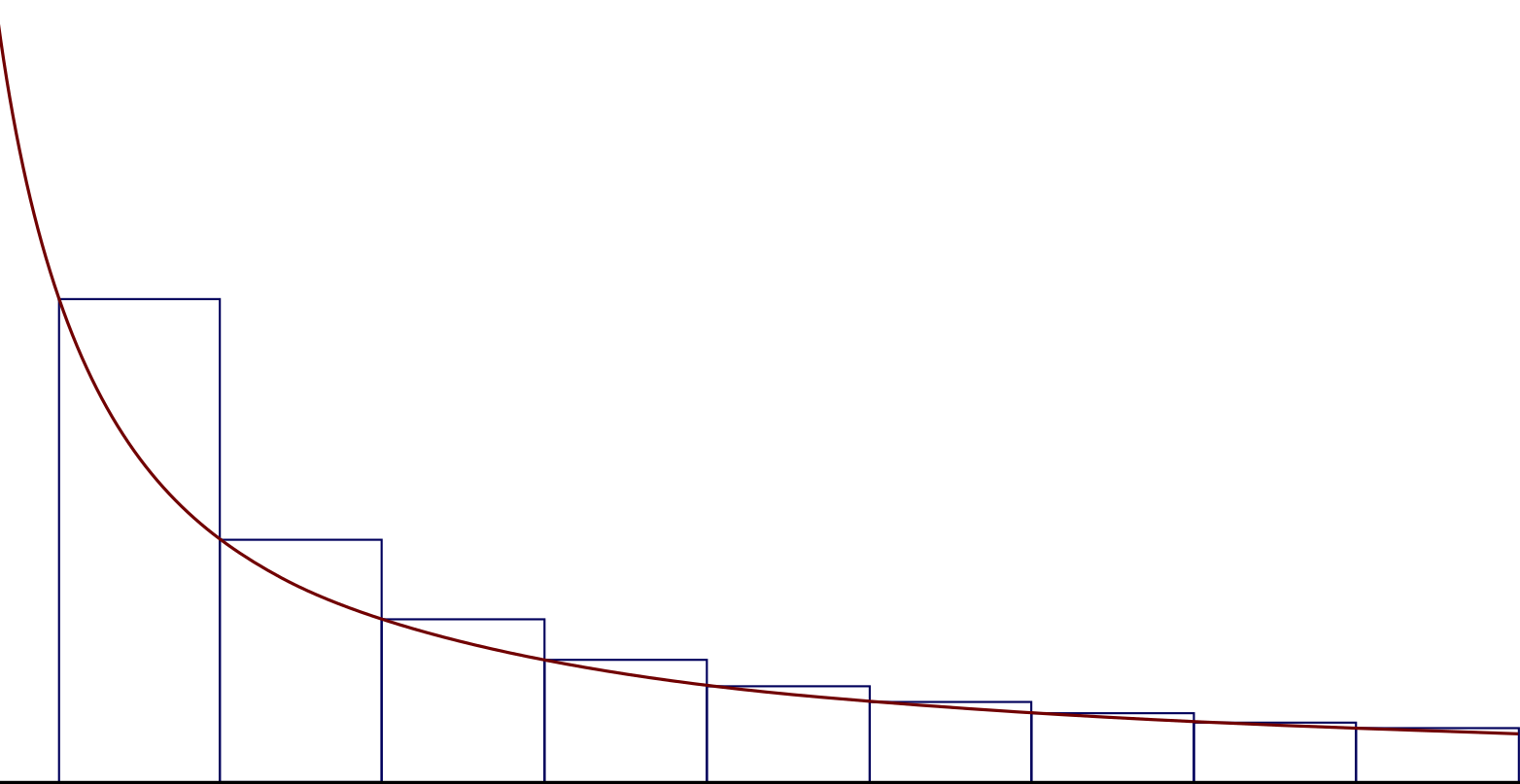
Abb.1: Linke Riemannsumme der Funktion
"Das Integral können wir ganz leicht berechnen", fährt Emmy fort.
"Das ging mir jetzt zu schnell! Wie hast du denn das Integral berechnet?", fragt Bertrand.
"Cool, das kann ich nun nach ableiten!", behauptet Carl und fängt an zu rechnen. Nach einem kurzen Moment zeigt er den anderen sein Ergebnis:
Carl fährt fort: "Wir brauchen also ein , so dass
Das gilt genau dann, wenn
Also muss gelten "
"Wir haben unser gefunden!", meint Maryam.
"Ist das nun auch ein Maximum der Funktion?", fragt Bertrand. "Es könnte ja auch ein Minimum oder ein Terrassenpunkt sein."
"Gute Frage! Lasst uns die Funktion aufmalen, dann sehen wir schon, ob unser ein Maximum ist", schlägt Carl vor.
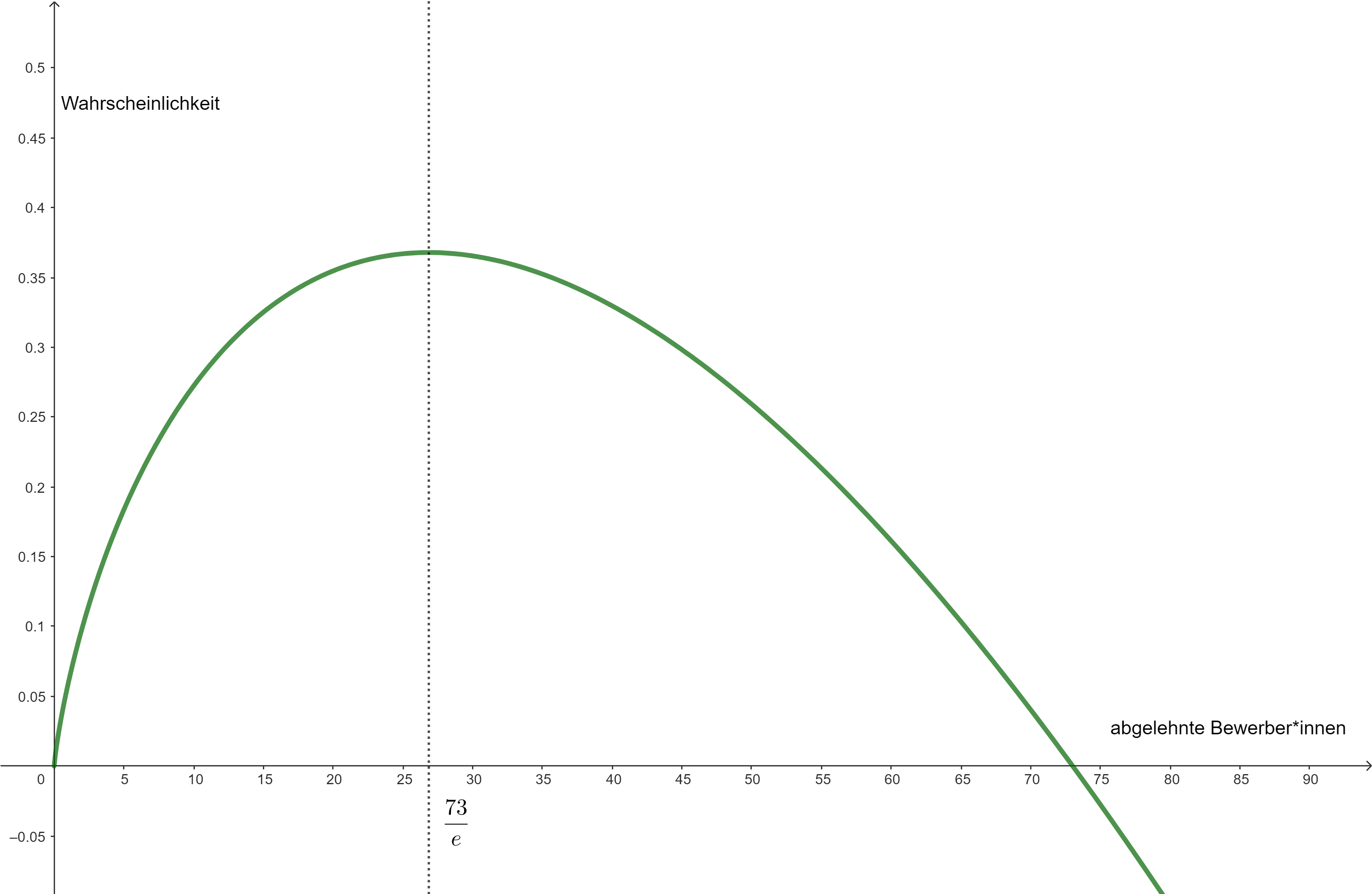
Graph der Funktion
"Ah, es gibt ein Maximum bei unserem . Das heißt, für ist die Erfolgswahrscheinlichkeit unserer Strategie maximal", meint Maryam.
"Das stimmt nicht ganz.", entgegnet Bertrand, "wir haben die Summe ja nicht genau bestimmt sondern nur abgeschätzt. Außerdem können wir in Echt nur als ganze Zahl wählen, aber bei uns ist
Wir können nicht Personen ablehnen, sondern nur oder ."
"Ok, alles ist nur abgeschätzt. Aber was ist denn nun die Wahrscheinlichkeit, dass die Strategie funktioniert, wenn wir wählen?", fragt Maryam.
"Wow, also mit einer Wahrscheinlichkeit von ungefähr finden wir mit der Strategie die beste Person!", ruft Carl.
Quellen:
Abb. 1: zugeschnittenes Bild Lefthand-Riemann-Sum-Integral-Test von Lazauya, CC BY-SA 4.0, via Wikimedia Commons
5 Anwendung der Strategie
Emmy, Maryam, Carl und Bertrand sind mit ihrer Strategie zufrieden und beschließen, sie auszuprobieren. Für ihre Bewerber*innen wollen sie zunächst Castings durchführen. Bertrand hat schon eine Tabelle vorbereitet, in der sie festhalten können, ab welchem Scoville-Grad jede dieser 27 Personen zu weinen anfängt.
27 Castings später haben sie die folgende Tabelle:
Nr. | Name | Beginnt zu weinen bei einem Scoville-Grad von ... |
|---|---|---|
Constantin | 5.000 | |
Sophie | 500 | |
Alexander | 10.000 | |
Peter | 2.500 |
Unter den 27 Castings war Alexander der beste Kandidat mit 10.000 Scoville. Von nun an werden alle Bewerber*innen mit diesem Ergebnis verglichen. Und in der Tat: Pierre-Simon, der 42. Bewerber, schlägt dieses Ergebnis mit beeindruckenden 20.000 Scoville. Mit (nicht nur Freuden-)Tränen in den Augen empfängt er die Nachricht, dass er ab nächstem Monat das Zimmer beziehen kann.
6 Einordnung und Ausblick
Die Aufgabe, aus einer Reihe einzeln betrachteter Bewerber den besten auszuwählen, wird “Sekretärinnenproblem” oder auch “Heiratsproblem” genannt. Es hat Verbindungen in die Statistik, Spieltheorie und Entscheidungstheorie.
Die von Emmy, Maryam, Carl und Bertrand gewählte Strategie nennt man “1/e-Regel” oder “37%-Regel”. Dabei schaut man sich zunächst der Bewerbungen an und akzeptiert danach die erste Person, die besser als alle bisherigen ist. Wir haben gesehen, dass die Wahrscheinlichkeit, auf diese Weise die beste Person zu wählen, mindestens beträgt.
Die 1/e-Regel ist sogar optimal: Es gibt keine Strategie, die eine größere Erfolgswahrscheinlichkeit hat. Das kann man mithilfe des Odds-Algorithmus zeigen, der im Jahr 2000 von Franz Thomas Bruss entwickelt wurde. Das Sekretärinnenproblem ist ein Spezialfall davon.
Bruss hat außerdem 1984 das "1/e-Gesetz der besten Wahl" bewiesen. Man sollte es nicht mit der “1/e-Regel” verwechseln, die Emmy, Maryam, Carl und Bertrand verwendet haben: Das 1/e-Gesetz der besten Wahl ist wesentlich allgemeiner. Es ist auch in nicht-diskreter Zeit und bei einer unbekannten Anzahl von Kandidaten anwendbar.
