Lösen Sie die folgenden Aufgaben:
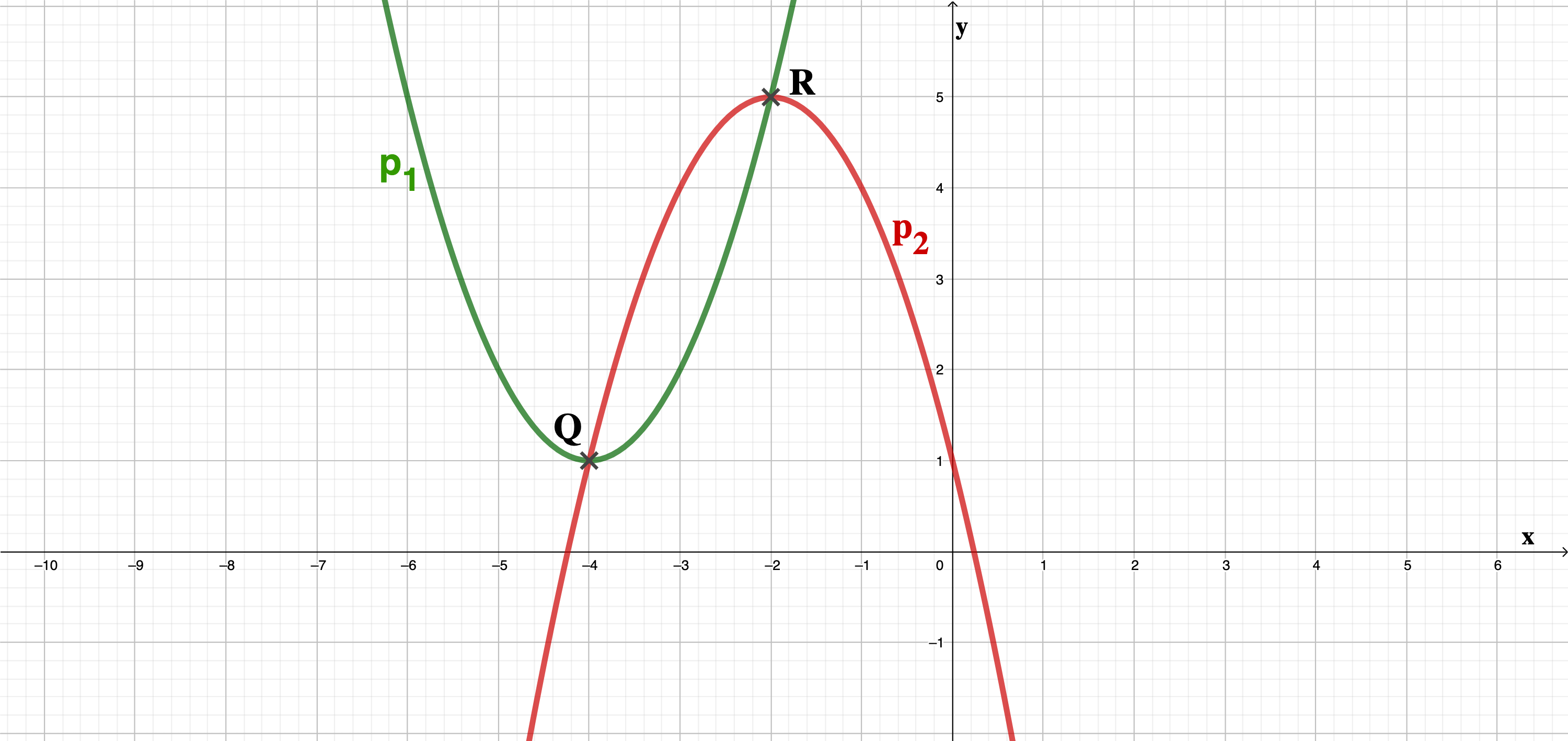
Ermitteln Sie rechnerisch die Funktionsgleichung der nach oben geöffneten Normalparabel mit dem Scheitelpunkt in der Normalform.
Die nach unten geöffnete Normalparabel geht durch die Punkte und . Ermitteln Sie rechnerisch die Funktionsgleichung von in der Scheitelpunktform und geben Sie den Scheitelpunkt an.
Bestimmen Sie zeichnerisch die Koordinaten der Schnittpunkte und der beiden Normalparabeln und in einem Koordinatensystem mit der Längeneinheit 1 cm. Geben Sie und an.
Die Normalparabeln sowie schneiden sich in den Punkten und . Berechnen Sie die Koordinaten von und und geben Sie beide Punkte an.