Die folgende Skizze zeigt die Fläche einer Werbetafel für eine Surfschule. Es gilt:
; ;
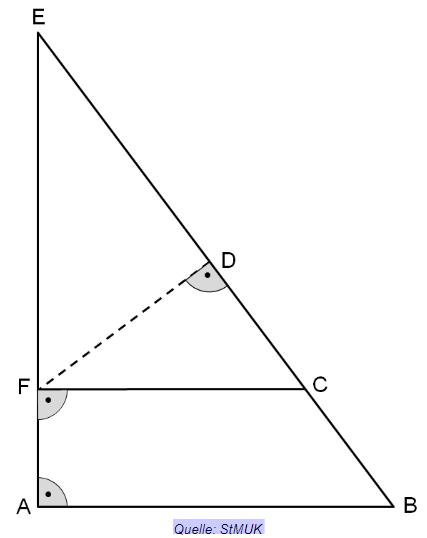
Hinweis: Skizze nicht maßstabsgetreu
Das Trapez ABCF der Werbetafel soll rot lackiert werden. Berechnen Sie den Flächeninhalt dieses Trapezes.
Der Umfang der Tafel soll entlang des Dreiecks ABE mit einem speziellen LED–Lichtschlauch beleuchtet werden. Diesen kann man nur bis zu einem Winkel von 25° biegen, damit er nicht bricht. Überprüfen Sie, ob der Lichtschlauch für dieses Dreieck geeignet ist.
