Aufgabe A 2
Gegeben ist das Viereck .
Es gilt: ; ; ; .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
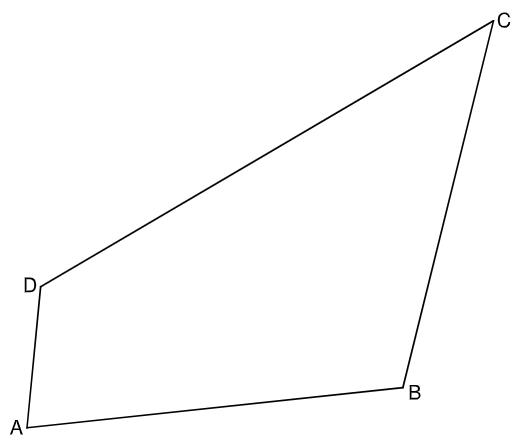
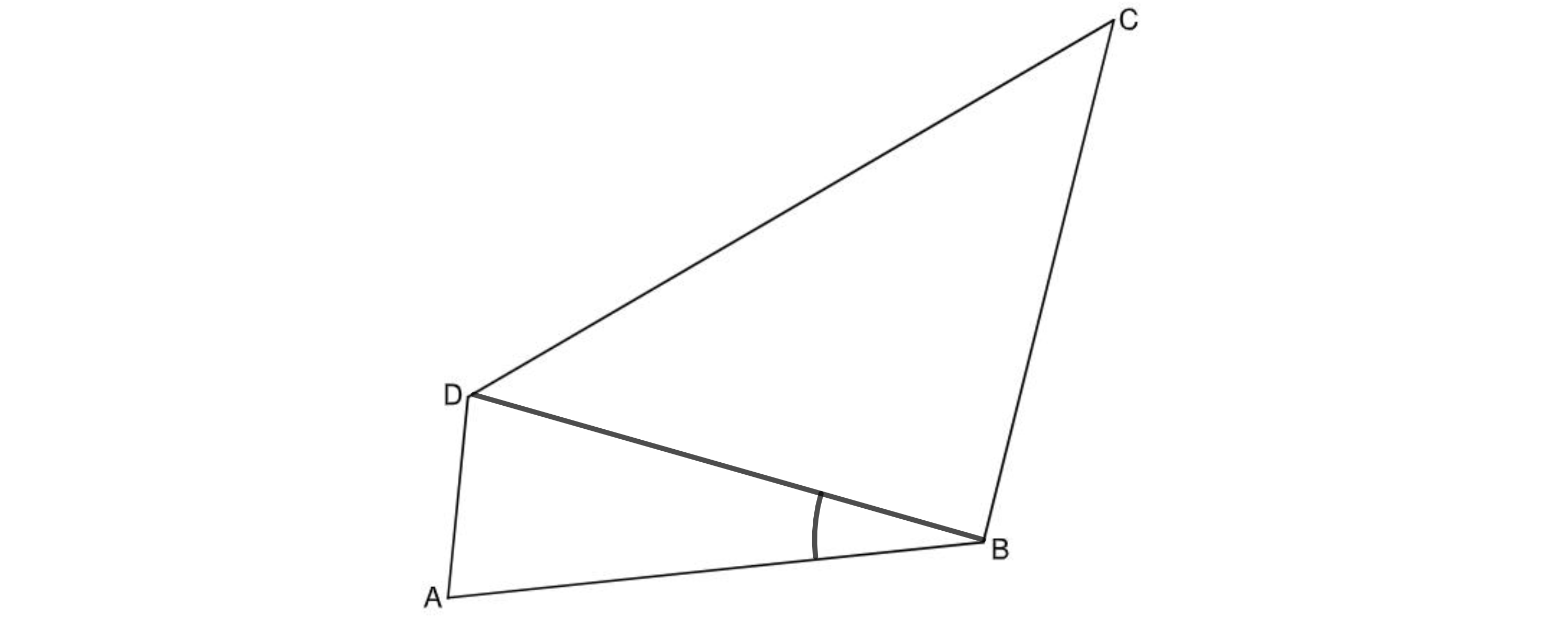
Zeichnen Sie die Strecke [BD] in die Zeichnung zu A 2.0 ein.
Berechnen Sie sodann das Maß des Winkels DBA und die Länge der Strecke [BD]. (3 P)
Teilergebnisse:
Berechnen Sie den Flächeninhalt des Vierecks . (2P)
Ergebnis
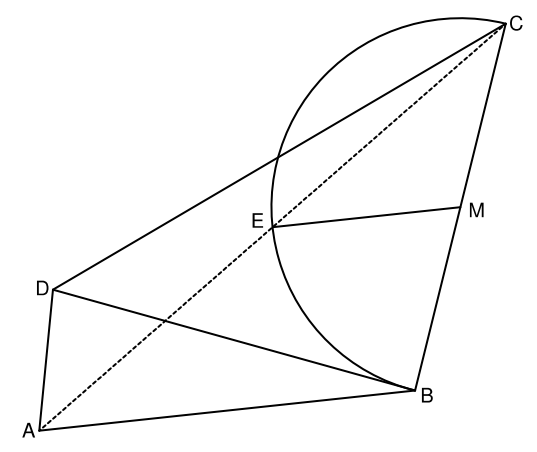
Der Punkt ist der Mittelpunkt der Strecke []. Der Kreisbogen mit dem Mittelpunkt schneidet die Strecke [] in den Punkten und .
Zeichnen Sie den Kreisbogen und Strecke [] in die Zeichnung zu 2) ein. (1 P)
Die Strecke [] ist parallel zur Strecke ].
Begründen Sie, weshalb für das Maß des Winkels gilt: .
Berechnen Sie sodann die Bogenlänge des Kreisbogens mit dem Mittelpunkt . (2 P)
cmBerechnen Sie den Flächeninhalt der Figur, die durch den Kreisbogen und die Strecken [] und [] begrenzt wird.
Bestimmen Sie sodann den prozentualen Anteil dieses Flächeninhalts am Flächeninhalt des Vierecks . (2 P)
%