Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe A 1
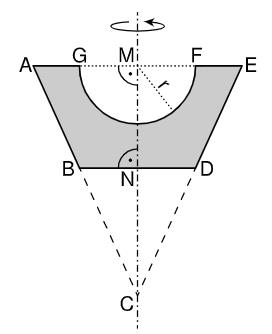
Die Vorlage eines Kerzenhalters für kugelförmige Kerzen ist ein Rotationskörper mit der Rotationsachse $MN$ . Die Skizze zeigt den Axialschnitt dieses Rotationskörpers. Der Punkt $C$ ist der Schnittpunkt der Geraden $AB$ und $ED$ .
Es gilt: $\overline{AE}=9\;\text{cm}$ ; $\overline{GF}= 5\;\text{cm}$ ; $\overline{BD}= 5\;\text{cm}$ ; ⁣ $\overline{CN}= 5{,}5\;\text{cm}$ ; $r =\overline{ MG}=\overline{ MF}$ ; $AE\Vert BD.$
1. Berechnen Sie das Volumen des Rotationskörpers.
  Runden Sie auf zwei Stellen nach dem Komma. (4 P)
  $[$ Zwischenergebnis: $\overline{CM}= 9{,}9\;\text{cm}$ ; Ergebnis: $V = 141{,}21\;\text{cm}^3$ $]$
2. Der Kerzenhalter soll aus Marmor gefertigt werden. $1\;\text{cm}^3$ des verwendeten Marmors hat eine Masse von $2{,}7 g$ .
  Berechnen Sie die Masse des Kerzenhalters. Runden Sie auf ganze Gramm. (1 P)
  g
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe A 2
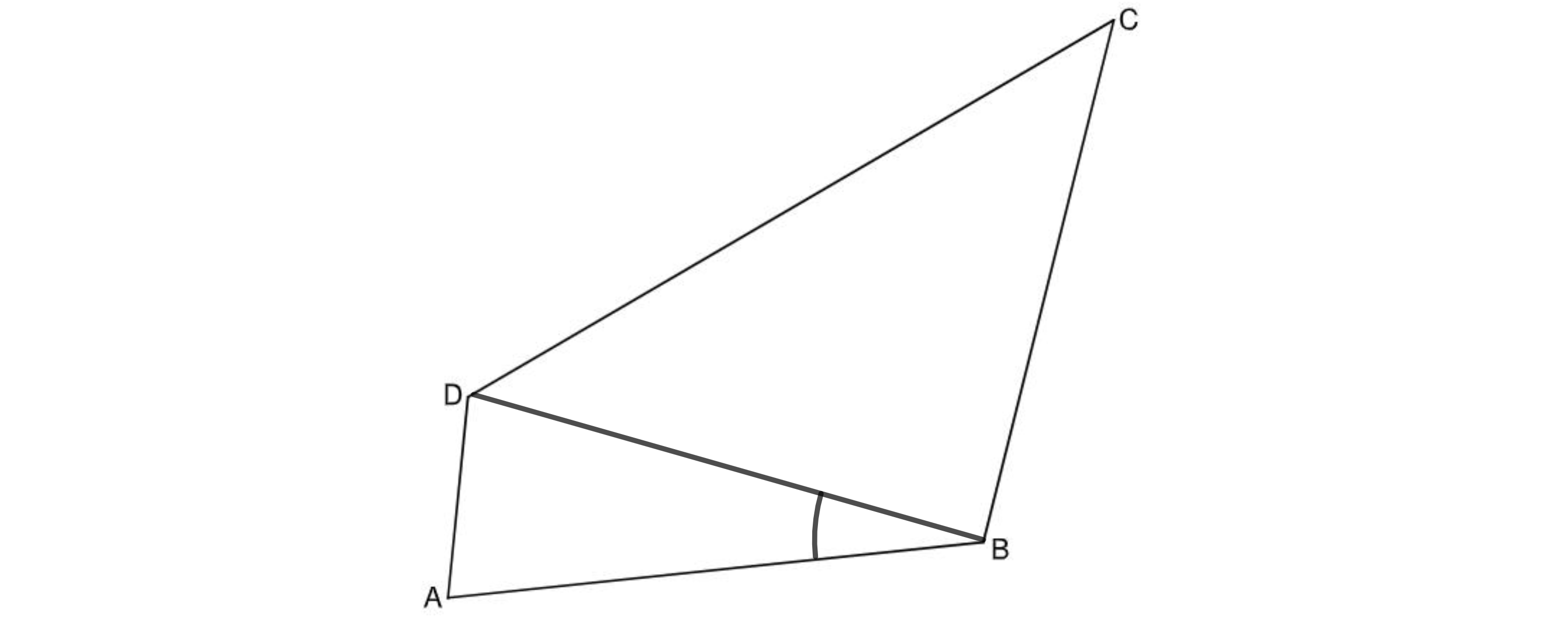
Gegeben ist das Viereck $ABCD$ .
Es gilt: $\overline{AB} = \overline{BC} = 8\;\text{cm}$ ; $\overline{AD}= 3 \;\text{cm}$ ; $\sphericalangle CBA= 110°$ ; $\sphericalangle{ADB} = 80°$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
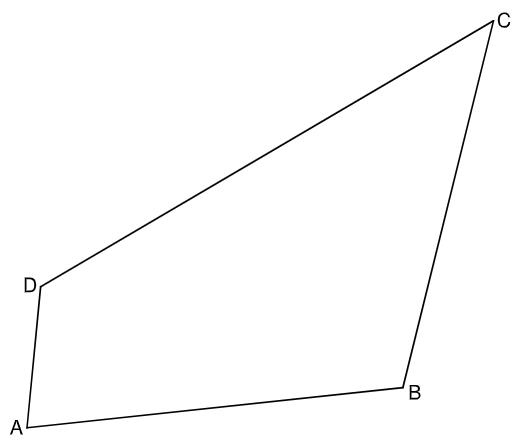
1. Zeichnen Sie die Strecke [BD] in die Zeichnung zu A 2.0 ein.
  Berechnen Sie sodann das Maß des Winkels DBA und die Länge der Strecke [BD]. (3 P)
  $[$ Teilergebnisse: $\sphericalangle DBA=21{,}67°; \overline{BD}=7{,}96\;\text{cm}]$
2. Berechnen Sie den Flächeninhalt des Vierecks $ABCD$ . (2P)
  $[$ Ergebnis $A_{ABCD}=43{,}58~\text{cm}^2$ $]$
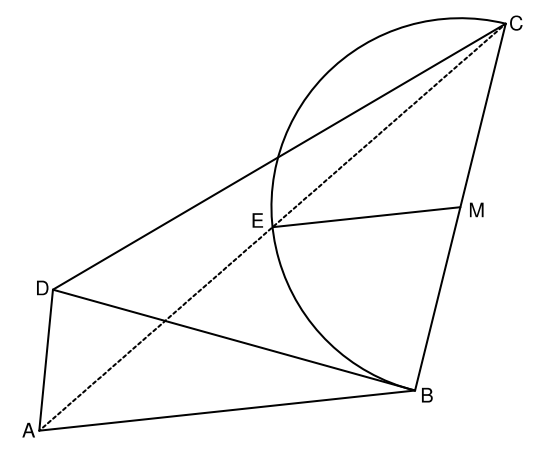
3. Der Punkt $M$ ist der Mittelpunkt der Strecke [ $BC$ ]. Der Kreisbogen $\overset\frown{CB}$ mit dem Mittelpunkt $M$ schneidet die Strecke [ $AC$ ] in den Punkten $C$ und $E$ .
  Zeichnen Sie den Kreisbogen $\overset\frown{CB}$ und Strecke [ $EM$ ] in die Zeichnung zu 2) ein. (1 P)
4. Die Strecke [ $EM$ ] ist parallel zur Strecke $[AB$ ].
  Begründen Sie, weshalb für das Maß des Winkels $EMB$ gilt: $\sphericalangle{EMB}=70°$ .
  Berechnen Sie sodann die Bogenlänge des Kreisbogens $\overset\frown{EB}$ mit dem Mittelpunkt $M$ . (2 P)
  cm
5. Berechnen Sie den Flächeninhalt der Figur, die durch den Kreisbogen $\overset\frown{EB}$ und die Strecken [ $EM$ ] und [ $BM$ ] begrenzt wird.
  Bestimmen Sie sodann den prozentualen Anteil dieses Flächeninhalts am Flächeninhalt des Vierecks $ABCD$ . (2 P)
  %
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe A 3
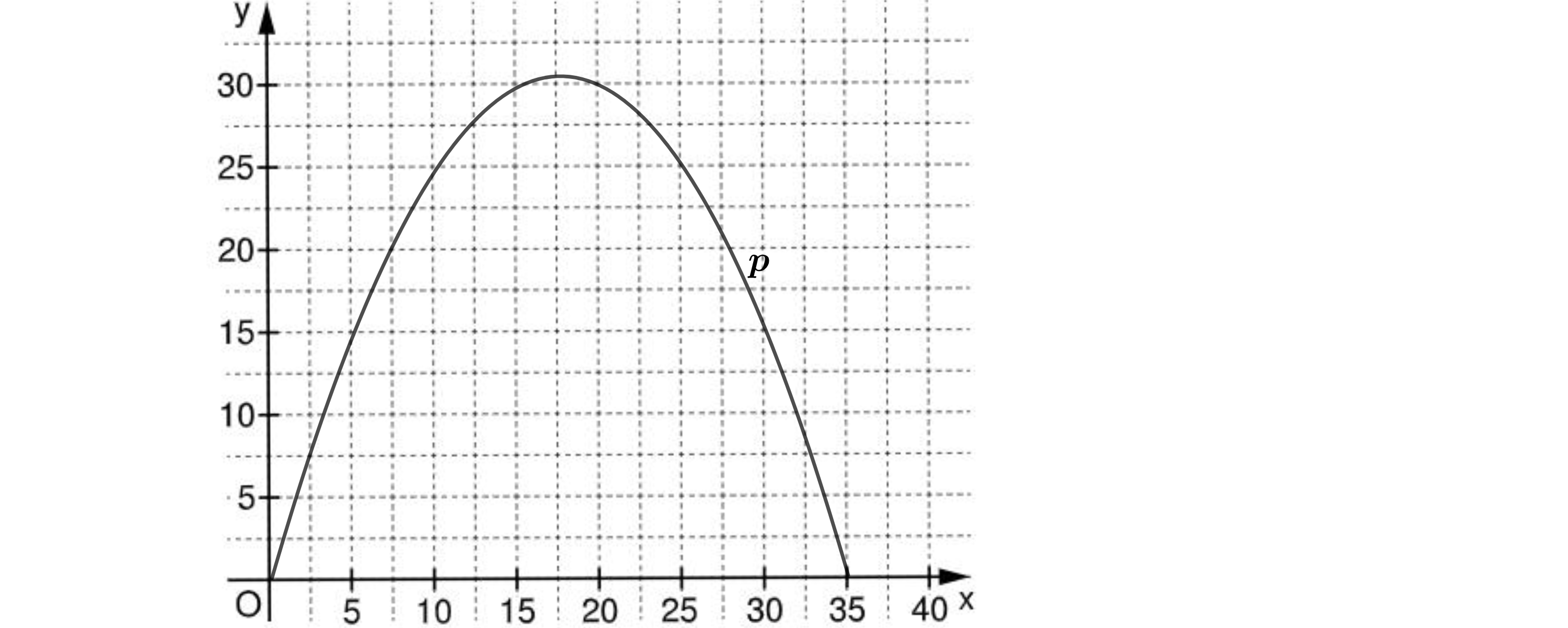
Ein Floh kann bezogen auf seine Körpergröße sehr weit und sehr hoch springen. Ein solcher Sprung kann näherungsweise durch die Parabel $p: y=-0{,}1x^2+3{,}5x$ , $(\mathbb{G}=\mathbb{R_0}^+\times\mathbb{R_0}^+)$
beschrieben werden. Dabei entspricht $x\;\text{cm}$ der horizontal gemessenen Entfernung vom Absprungpunkt $P(0|0)$ und $y\;\text{cm}$ der zugehörigen Höhe über dem Boden. Der Floh landet im Punkt $Q(x_Q|0)$ auf dem Boden.
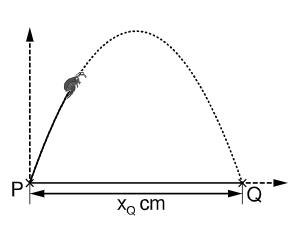
1. Berechnen Sie die Koordinaten des Scheitelpunkts $S$ der Parabel $p$ . Zeichnen Sie sodann die Parabel $p$ für $x\in[0;x_Q]$ in das Koordinatensystem ein. (3 P)
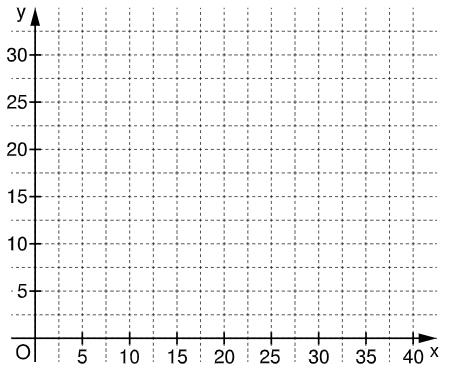
2. Geben Sie die maximale Höhe und die Weite dieses Sprungs an.
  Runden Sie auf ganze Zentimeter. (1 P)
3. Der unten abgebildete Floh kann bis zu $0{,}6\;\text{m}$ weit springen. Kreuzen Sie an, wie weit ein $1{,}80\;\text{m}$ großer Mensch ungefähr springen würde, wenn er im Verhältnis zu seiner Körpergröße genauso weit wie dieser Floh springen könnte.
  Kreuze die entsprechende Antwort an. (1 P)
  3,6m
  36m
  360m
  3600m

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Teil A

Aufgabe A 1

Aufgabe A 2

Aufgabe A 3