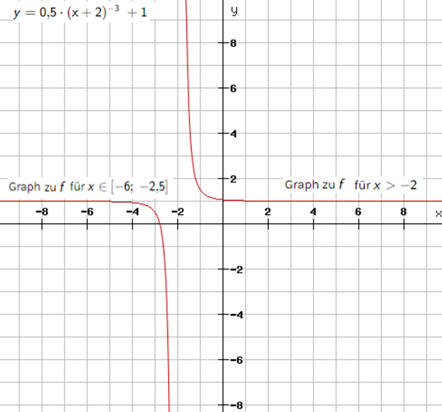
Gegeben ist die Funktion mit der Gleichung . Im Koordinatensystem ist für der Graph zu eingezeichnet.
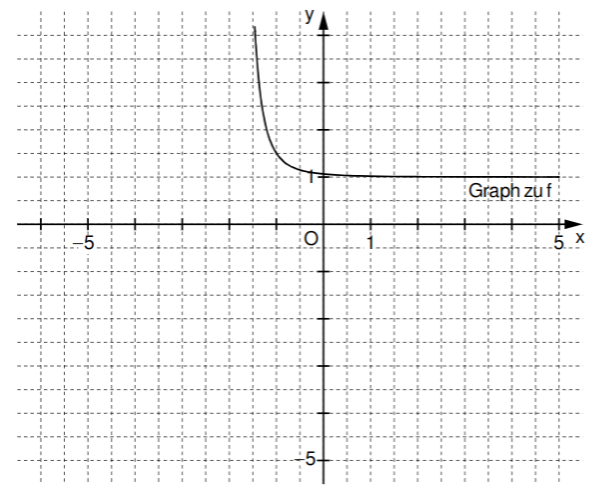
Zeichnen Sie für den Graphen zu in das Koordinatensystem zur Aufgabenstellung ein und geben Sie die Wertemenge von an.
Punkte mit der Abszisse liegen auf dem Graphen zu mit .
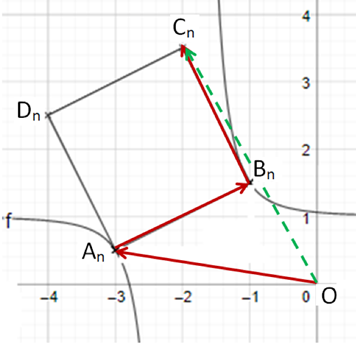
Sie legen mit Punkten und Quadrate fest.
Die x-Koordinate der Punkte ist um 2 größer als die Abszisse der Punkte , die y-Koordinate der Punkte ist um 1 größer als die -Koordinate der Punkte Zeichnen Sie die Quadrate für und für
in das Koordinatensystem zu 2.0.
Begründen Sie, weshalb alle Quadrate den gleichen Flächeninhalt haben, und geben Sie diesen an.
Zeigen Sie, dass für die Koordinaten der Punkte in Abhängigkeit von der Abszisse der Punkte gilt: .
Der Punkt des Quadrats liegt auf der –Achse. Geben Sie die Koordinaten des Punktes an.