Teil A - lernen mit Serlo!

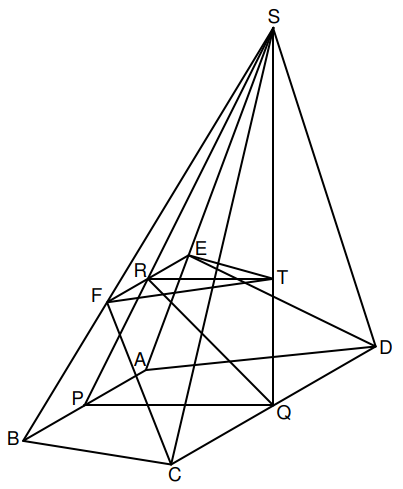
Das Schrägbild zeigt die Pyramide $ABCDS$ mit dem gleichschenkligen Trapez $ABCD$ als Grundfläche und der Höhe $[QS]$ . Der Punkt $P$ ist der Mittelpunkt der Strecke $[AB]$ und der Punkt $Q$ ist der Mittelpunkt der Strecke $[CD]$ .

Es gilt: $[AB]||[CD];\overline{AB}=6\ \text{cm};\overline{CD}=10\ \text{cm};\overline{QS}=8\ \text{cm};\overline{PQ}=4\ \text{cm}$ . Der Punkt $R$ liegt auf der Strecke $[PS]$ mit $\overline {PR}=3 \textrm{ cm}$ . Er ist der Mittelpunkt der Strecke $[EF]\textrm{ mit }E\in[AS], F\in[BS]\ \textrm{und}\ [EF]||[AB]$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

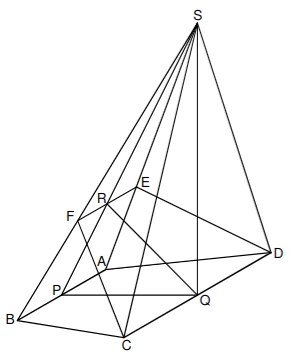
Berechnen Sie die Längen der Strecken $[PS]$ und $[EF]$ .

$[$ Ergebnis: $\overline{PS}=8{,}94\ \textrm{cm}$ ; $\overline{EF}=3{,}99\ \textrm{cm}]$

Berechnen Sie den Flächeninhalt $A$ des Trapezes $CDEF$ .

$[$ Zwischenergebnis: $\measuredangle QPS=63{,}43°]$

Um den Flächeninhalt eines Trapezes zu berechnen benötigst du die Längen, der zueinander parallelen Seiten (diese kennst du schon: $\overline{EF} = 3{,}99\ \text{cm}$ und $\overline{CD} = 10\ \text{cm}$ ), sowie die Länge der Höhe. Die Höhe ist im Trapez $CDEF$ durch die Strecke $[QR]$ gegeben, die Länge dieser Strecke musst du noch berechnen.

Um $\overline{QR}$ zu berechnen kannst du zum Beispiel das Dreieck $PQR$ betrachten, das wiederum im Dreieck $PQS$ liegt:

Du kennst bereits die Seitenlängen $\overline{PQ} = 4\;\text{cm}$ und $\overline{PR} = 3\;\text{cm}$ . Wenn du jetzt noch den Wert des Winkels $\sphericalangle QPR$ (bzw. $\sphericalangle QPS$ ) herausfindest, dann kannst du den Kosinussatz verwenden, um $\overline {QR}$ zu erhalten.

Um den Wert von $\sphericalangle QPS$ zu bestimmen, kannst du den Tangens im rechtwinkligen Dreieck $PQS$ verwenden (es funktioniert aber genauso gut mit Sinus oder Kosinus):

$\displaystyle \tan (\measuredangle PQS)$	$=$	$\displaystyle \frac{\overline{QS}}{\overline{PQ}}$
	↓	Setze die bekannten Längen ein.
	$=$	$\displaystyle \frac{8}{4}$	$\displaystyle \tan ^{-1}()$
	↓	Wende die Umkehrfunktion des Tangens an.
$\displaystyle \measuredangle QPS$	$=$	$\displaystyle \tan ^{-1}(2)$
$\displaystyle \measuredangle QPS$	$=$	$\displaystyle 63{,}43°$

Nun wendest du noch den Kosinussatz an und erhältst damit $\overline{QR}$ :

$\displaystyle \overline{QR}^2$	$=$	$\displaystyle \overline{PQ}^2+\overline{PR}^2-2\cdot \overline{PQ}\cdot \overline{PR}\cdot \cos (\measuredangle PQR)$
	↓	Setze die Werte ein.
$\displaystyle \overline{QR}^2$	$=$	$\displaystyle (4\ \text{cm})^2+(3\ \text{cm})^2-2\cdot (4\ \text{cm})\cdot (3\ \text{cm})\cdot \cos (63{,}43°)$
$\displaystyle \overline{QR}^2$	$=$	$\displaystyle 14{,}27\ \text{cm}^2$	$\displaystyle \sqrt{ }$
$\displaystyle \overline{QR}$	$=$	$\displaystyle 3{,}78\ \text{cm}$

Damit hast du jetzt alles, was du brauchst, um den Flächeninhalt des Trapezes mit der Formel zu berechnen:

$A_{CDEF} = \frac12 (\overline{AB} + \overline{CD}) \cdot \overline{QR} = \frac12(3{,}99\ \text{cm} + 10\ \text{cm})\cdot (3{,}78\ \text{cm}) = 26{,}44\ \text{cm}^2$

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Der Punkt $T$ liegt auf der Strecke $[QS]$ mit $[RT]||[PQ]$ . Das Dreieck $EFT$ ist die Grundfläche der Pyramide $EFTS$ mit der Spitze $S.$

Zeichnen Sie die Pyramide $E$ $FTS$ in das Schrägbild zur Aufgabenstellung ein. Berechnen Sie sodann das Volumen $V$ der Pyramide $EFTS$ .

Einzeichnen der Pyramide $E$ $FTS$ in das Schrägbild

Für das Pyramidenvolumen gilt:

$V=\dfrac{1}{3}\cdot G\cdot h=\dfrac{1}{3}\cdot\dfrac{1}{2}\cdot \overline{EF}\cdot \overline{RT}\cdot \overline{ST}$

In Aufgabe a) wurde $\overline{EF}=3{,}99\;\text{cm}$ berechnet. Es müssen noch die Strecken $\overline{RT}$ und $\overline{ST}$ berechnet werden. In Aufgabe b) wurde der Winkel $\measuredangle QPS=63{,}43°$ berechnet. Es gilt: $\measuredangle TRS= \measuredangle QPS=63{,}43°$

Im Dreieck $RTS$ kann der Kosinus angewendet werden:

$\displaystyle \cos\measuredangle TRS$	$=$	$\displaystyle \frac{\overline{RT}}{\overline{RS}}$
	$=$	$\displaystyle \frac{\overline{RT}}{\overline{PS}-\overline{PR}}$
	↓	Setze die Werte ein.
$\displaystyle \cos63{,}43^\circ$	$=$	$\displaystyle \dfrac{\overline{RT}}{(8{,}94-3)}$	$\displaystyle \cdot (8{,}94-3)$
$\displaystyle \cos63{,}43^\circ \cdot (8{,}94-3)$	$=$	$\displaystyle \overline{RT}$
$\displaystyle 2{,}66$	$≈$	$\displaystyle \overline{RT}$

Damit ist $\overline{RT}=2{,}66~\text{cm}$ .

Im Dreieck $RTS$ kann der Sinus angewendet werden:

$\displaystyle \sin\measuredangle TRS$	$=$	$\displaystyle \frac{\overline{ST}}{\overline{RS}}$
	$=$	$\displaystyle \dfrac{\overline{ST}}{\overline{PS}-\overline{PR}}$
	↓	Setze die Werte ein.
$\displaystyle \sin63{,}43^\circ$	$=$	$\displaystyle \dfrac{\overline{ST}}{(8{,}94-3)}$	$\displaystyle \cdot (8{,}94-3)$
$\displaystyle \sin63{,}43^\circ \cdot (8{,}94-3)$	$=$	$\displaystyle \overline{ST}$
$\displaystyle 5{,}31$	$≈$	$\displaystyle \overline{ST}$

Damit ist $\overline{ST}=5{,}31~\text{cm}$ .

Setze alle Werte in die Volumenformel ein:

$\displaystyle V$	$=$	$\displaystyle \dfrac{1}{3}\cdot\dfrac{1}{2}\cdot \overline{EF}\cdot \overline{RT}\cdot \overline{ST}$
	↓	Setze alle Werte ein.
	$=$	$\displaystyle \dfrac{1}{3}\cdot\dfrac{1}{2}\cdot 3{,}99\;\text{cm}\cdot 2{,}66\;\text{cm}\cdot 5{,}31\;\text{cm}$
	$≈$	$\displaystyle 9{,}39\;\text{cm}^3$

Das Volumen der Pyramide $EFTS$ beträgt $9{,}39\;\text{cm}^3$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

$\displaystyle \frac{\color{ff6600}{\overline{EF}}}{\color{006400}{\overline{AB}}}$	$=$	$\displaystyle \frac{\color{009999}{\overline{RS}}}{\color{660099}\overline{PS}}$
$\displaystyle \frac{\overline{EF}}{6\ \text{cm}}$	$=$	$\displaystyle \frac{8{,}94\ \text{cm}-3\ \text{cm}}{8{,}94\ \text{cm}}$	$\displaystyle \cdot 6\ \text{cm}$
$\displaystyle \overline{EF}$	$=$	$\displaystyle \frac{5{,}94\ \text{cm}\cdot 6\ \text{cm}}{8{,}94\ \text{cm}}$
$\displaystyle \overline{EF}$	$=$	$\displaystyle 3{,}99\;\text{cm}$