Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Am $22.02.2020$ kaufte sich Claudia für $2000\;€$ Aktien. Sie geht davon aus, dass der Wert $y\;€$ ihrer Aktien nach $\textrm{x}$ Jahren durch die Funktion $\textrm{f}: \textrm{y}=2000\cdot 1{,}07^\textrm{x}$ mit $(\mathbb{G}=\mathbb{R_0^\textrm{+}}\times\mathbb{R_0 ^\textrm{+}})$ dargestellt werden kann.
1. Ergänzen Sie die Wertetabelle auf Ganze gerundet. Zeichnen Sie sodann den Graphen zu $f$ in das Koordinatensystem ein.
  
  Die Wertetabelle sollte so aussehen:
  x
  0
  5
  10
  15
  20
  25
  $f(x)$
  $2000$
  $2805$
  $3934$
  $5518$
  $7739$
  $10854$
  Diese Punkte kannst du jetzt einfach in das Koordinatensystem eintragen und miteinander verbinden:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
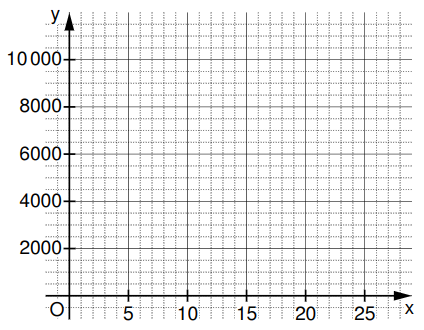
2. Ergänzen Sie die folgende Aussage. Claudia nimmt an, dass der Wert ihrer Aktien jährlich um ____ Prozent zunimmt.
  
  Claudia multipliziert den Anfangswert ihrer Aktien mit dem Faktor $1{,}07^x$ , sie geht also davon aus, dass der Wert ihrer Aktien jährlich um $7\;\%$ zunimmt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Ermitteln Sie mithilfe des Graphen, nach welcher Zeit sich das Anfangskapital verfünffacht hätte.
  
  Das fünffache des Anfangskapitals sind $5\cdot2000\;€=10000\;€$ . Suche jetzt die Stelle auf dem Graphen, an dem der y-Wert $10000$ beträgt und lies den entsprechenden x-Wert ab:
  Aus der Zeichnung kann man erkennen, dass der x-Wert ungefähr bei $23{,}..$ liegt. Wirklich verfünffacht hat sich das Anfangskapital dann also nach 24 Jahren.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Claudia plant, am $22.02.2065$ in den Ruhestand zu gehen. Bestimmen Sie rechnerisch, wie viel ihre Aktien zu diesem Zeitpunkt nach der oben getroffenen Annahme wert wären. Runden Sie auf ganze Euro.
  
  Am $22.02.2065$ sind $45$ Jahre vergangen, seit Claudia die Aktien gekauft hat. Um herauszufinden, wie viel ihre Aktien dann wert sind, setzt du einfach den Wert $45$ in die Funktion ein und erhältst:
  $f(45)=2000\cdot1{,}07^{45}=42004{,}90$
  Nach der Annahme sind die Aktien zu Claudias Ruhestand also etwa $42005\;€$ wert.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

x	0	5	10	15	20	25
$f(x)$	$2000$	$2805$	$3934$	$5518$	$7739$	$10854$

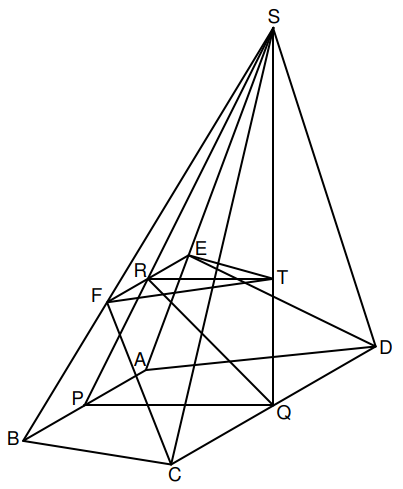
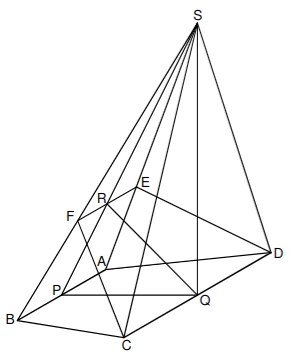
Das Schrägbild zeigt die Pyramide $ABCDS$ mit dem gleichschenkligen Trapez $ABCD$ als Grundfläche und der Höhe $[QS]$ . Der Punkt $P$ ist der Mittelpunkt der Strecke $[AB]$ und der Punkt $Q$ ist der Mittelpunkt der Strecke $[CD]$ .

Es gilt: $[AB]||[CD];\overline{AB}=6\ \text{cm};\overline{CD}=10\ \text{cm};\overline{QS}=8\ \text{cm};\overline{PQ}=4\ \text{cm}$ . Der Punkt $R$ liegt auf der Strecke $[PS]$ mit $\overline {PR}=3 \textrm{ cm}$ . Er ist der Mittelpunkt der Strecke $[EF]\textrm{ mit }E\in[AS], F\in[BS]\ \textrm{und}\ [EF]||[AB]$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Berechnen Sie die Längen der Strecken $[PS]$ und $[EF]$ .

$[$ Ergebnis: $\overline{PS}=8{,}94\ \textrm{cm}$ ; $\overline{EF}=3{,}99\ \textrm{cm}]$

Berechnen Sie den Flächeninhalt $A$ des Trapezes $CDEF$ .

$[$ Zwischenergebnis: $\measuredangle QPS=63{,}43°]$

Um den Flächeninhalt eines Trapezes zu berechnen benötigst du die Längen, der zueinander parallelen Seiten (diese kennst du schon: $\overline{EF} = 3{,}99\ \text{cm}$ und $\overline{CD} = 10\ \text{cm}$ ), sowie die Länge der Höhe. Die Höhe ist im Trapez $CDEF$ durch die Strecke $[QR]$ gegeben, die Länge dieser Strecke musst du noch berechnen.

Um $\overline{QR}$ zu berechnen kannst du zum Beispiel das Dreieck $PQR$ betrachten, das wiederum im Dreieck $PQS$ liegt:

Du kennst bereits die Seitenlängen $\overline{PQ} = 4\;\text{cm}$ und $\overline{PR} = 3\;\text{cm}$ . Wenn du jetzt noch den Wert des Winkels $\sphericalangle QPR$ (bzw. $\sphericalangle QPS$ ) herausfindest, dann kannst du den Kosinussatz verwenden, um $\overline {QR}$ zu erhalten.

Um den Wert von $\sphericalangle QPS$ zu bestimmen, kannst du den Tangens im rechtwinkligen Dreieck $PQS$ verwenden (es funktioniert aber genauso gut mit Sinus oder Kosinus):

$\displaystyle \tan (\measuredangle PQS)$	$=$	$\displaystyle \frac{\overline{QS}}{\overline{PQ}}$
	↓	Setze die bekannten Längen ein.
	$=$	$\displaystyle \frac{8}{4}$	$\displaystyle \tan ^{-1}()$
	↓	Wende die Umkehrfunktion des Tangens an.
$\displaystyle \measuredangle QPS$	$=$	$\displaystyle \tan ^{-1}(2)$
$\displaystyle \measuredangle QPS$	$=$	$\displaystyle 63{,}43°$

Nun wendest du noch den Kosinussatz an und erhältst damit $\overline{QR}$ :

$\displaystyle \overline{QR}^2$	$=$	$\displaystyle \overline{PQ}^2+\overline{PR}^2-2\cdot \overline{PQ}\cdot \overline{PR}\cdot \cos (\measuredangle PQR)$
	↓	Setze die Werte ein.
$\displaystyle \overline{QR}^2$	$=$	$\displaystyle (4\ \text{cm})^2+(3\ \text{cm})^2-2\cdot (4\ \text{cm})\cdot (3\ \text{cm})\cdot \cos (63{,}43°)$
$\displaystyle \overline{QR}^2$	$=$	$\displaystyle 14{,}27\ \text{cm}^2$	$\displaystyle \sqrt{ }$
$\displaystyle \overline{QR}$	$=$	$\displaystyle 3{,}78\ \text{cm}$

Damit hast du jetzt alles, was du brauchst, um den Flächeninhalt des Trapezes mit der Formel zu berechnen:

$A_{CDEF} = \frac12 (\overline{AB} + \overline{CD}) \cdot \overline{QR} = \frac12(3{,}99\ \text{cm} + 10\ \text{cm})\cdot (3{,}78\ \text{cm}) = 26{,}44\ \text{cm}^2$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Der Punkt $T$ liegt auf der Strecke $[QS]$ mit $[RT]||[PQ]$ . Das Dreieck $EFT$ ist die Grundfläche der Pyramide $EFTS$ mit der Spitze $S.$

Zeichnen Sie die Pyramide $E$ $FTS$ in das Schrägbild zur Aufgabenstellung ein. Berechnen Sie sodann das Volumen $V$ der Pyramide $EFTS$ .

Einzeichnen der Pyramide $E$ $FTS$ in das Schrägbild

Für das Pyramidenvolumen gilt:

$V=\dfrac{1}{3}\cdot G\cdot h=\dfrac{1}{3}\cdot\dfrac{1}{2}\cdot \overline{EF}\cdot \overline{RT}\cdot \overline{ST}$

In Aufgabe a) wurde $\overline{EF}=3{,}99\;\text{cm}$ berechnet. Es müssen noch die Strecken $\overline{RT}$ und $\overline{ST}$ berechnet werden. In Aufgabe b) wurde der Winkel $\measuredangle QPS=63{,}43°$ berechnet. Es gilt: $\measuredangle TRS= \measuredangle QPS=63{,}43°$

Im Dreieck $RTS$ kann der Kosinus angewendet werden:

$\displaystyle \cos\measuredangle TRS$	$=$	$\displaystyle \frac{\overline{RT}}{\overline{RS}}$
	$=$	$\displaystyle \frac{\overline{RT}}{\overline{PS}-\overline{PR}}$
	↓	Setze die Werte ein.
$\displaystyle \cos63{,}43^\circ$	$=$	$\displaystyle \dfrac{\overline{RT}}{(8{,}94-3)}$	$\displaystyle \cdot (8{,}94-3)$
$\displaystyle \cos63{,}43^\circ \cdot (8{,}94-3)$	$=$	$\displaystyle \overline{RT}$
$\displaystyle 2{,}66$	$≈$	$\displaystyle \overline{RT}$

Damit ist $\overline{RT}=2{,}66~\text{cm}$ .

Im Dreieck $RTS$ kann der Sinus angewendet werden:

$\displaystyle \sin\measuredangle TRS$	$=$	$\displaystyle \frac{\overline{ST}}{\overline{RS}}$
	$=$	$\displaystyle \dfrac{\overline{ST}}{\overline{PS}-\overline{PR}}$
	↓	Setze die Werte ein.
$\displaystyle \sin63{,}43^\circ$	$=$	$\displaystyle \dfrac{\overline{ST}}{(8{,}94-3)}$	$\displaystyle \cdot (8{,}94-3)$
$\displaystyle \sin63{,}43^\circ \cdot (8{,}94-3)$	$=$	$\displaystyle \overline{ST}$
$\displaystyle 5{,}31$	$≈$	$\displaystyle \overline{ST}$

Damit ist $\overline{ST}=5{,}31~\text{cm}$ .

Setze alle Werte in die Volumenformel ein:

$\displaystyle V$	$=$	$\displaystyle \dfrac{1}{3}\cdot\dfrac{1}{2}\cdot \overline{EF}\cdot \overline{RT}\cdot \overline{ST}$
	↓	Setze alle Werte ein.
	$=$	$\displaystyle \dfrac{1}{3}\cdot\dfrac{1}{2}\cdot 3{,}99\;\text{cm}\cdot 2{,}66\;\text{cm}\cdot 5{,}31\;\text{cm}$
	$≈$	$\displaystyle 9{,}39\;\text{cm}^3$

Das Volumen der Pyramide $EFTS$ beträgt $9{,}39\;\text{cm}^3$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die untenstehende Skizze zeigt das Dreieck $ABC$ mit $\overline{AB}=7\;\textrm{cm},\overline{BC}=5\;\textrm{cm}$ und $\measuredangle{ACB}=40°$ . Die Strecke $[DE]$ wird durch die Punkte $D\in[AC]$ und $E\in[BC]$ festgelegt. Es gilt: $[AB]||[DE];\overline{DE}=3{,}6\;\textrm{cm}$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
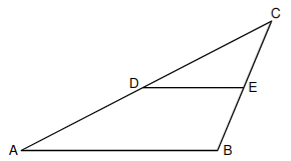
1. Berechnen Sie die Länge der Strecke $[BE]$ .
  $[$ Ergebnis: $\overline{BE}=2{,}43\;\textrm{cm}]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz
  Lösung Teilaufgabe a
  $\overline{BE}=\overline{BC}-\overline{EC}$
  Berechne zunächst $\overline{EC}$ und verwende hierfür den Strahlensatz.
  $\dfrac{\overline{EC}}{\overline{BC}}=\dfrac{\overline{DE}}{\overline{AB}}$
  $\dfrac{\overline{EC}}{5\;\textrm{cm}}=\dfrac{3{,}6\;\textrm{cm}}{7\;\textrm{cm}}$
  $\overline{EC}=2{,}57\;\textrm{cm}$
  $\overline{BE}=5\;\textrm{cm}-2{,}57\;\textrm{cm}=2{,}43\;\textrm{cm}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Berechnen Sie den Abstand $d$ der Strecken $[AB]\textrm{und}[DE]$ .
  
  Lösung Teilaufgabe b
  $d$ ist der Abstand der Strecken [AB] und [DE].
  Dann gilt:
  $\cos\left(\sphericalangle CBA-90°\right)= \dfrac{d}{\overline{BE}}$
  Um den Winkel $\sphericalangle CBA$ zu bestimmen, berechne zunächst den Winkel $\sphericalangle BAC$ . Wende hierzu den Sinussatz auf das Dreieck $ACB$ an.
  $$
  $\dfrac{\sin( \sphericalangle BAC)}{\overline{BC}}=\dfrac{\sin40°}{7\;\textrm{cm}}$
  $\dfrac{\sin( \sphericalangle BAC)}{\overline{5\;\textrm{cm}}}=\dfrac{\sin40°}{7\;\textrm{cm}}$
  $\sin( \sphericalangle BAC)=\dfrac{\sin40°\cdot 5\;\textrm{cm}}{7\;\textrm{cm}}=\dfrac{3{,}2139\;\textrm{cm}}{7\;\textrm{cm}}=0{,}4591$ $$
  $\sphericalangle BAC=\sin^{-1}(0{,}4591)=27{,}33°$
  Da die Winkelsumme im Dreieck $180°$ beträgt, ergibt sich
  $\sphericalangle CBA=180°-40°-27{,}33°=112{,}67°$
  $\cos(112{,}67°-90°)=\dfrac{d}{2{,}43\;\text{cm}}$
  $d=\cos(22{,}67°)\cdot 2{,}43\;\text{cm}=2{,}24\;\text{cm}$
  Der Abstand $d$ der Strecken $[AB]$ und $[DE]$ beträgt $2{,}24\;\text{cm}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \frac{\color{ff6600}{\overline{EF}}}{\color{006400}{\overline{AB}}}$	$=$	$\displaystyle \frac{\color{009999}{\overline{RS}}}{\color{660099}\overline{PS}}$
$\displaystyle \frac{\overline{EF}}{6\ \text{cm}}$	$=$	$\displaystyle \frac{8{,}94\ \text{cm}-3\ \text{cm}}{8{,}94\ \text{cm}}$	$\displaystyle \cdot 6\ \text{cm}$
$\displaystyle \overline{EF}$	$=$	$\displaystyle \frac{5{,}94\ \text{cm}\cdot 6\ \text{cm}}{8{,}94\ \text{cm}}$
$\displaystyle \overline{EF}$	$=$	$\displaystyle 3{,}99\;\text{cm}$

Teil A

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösung Teilaufgabe a

Hast du eine Frage oder Feedback?

Lösung Teilaufgabe b

Hast du eine Frage oder Feedback?