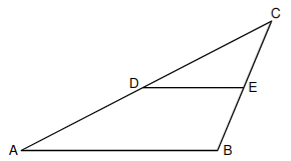
Lösung Teilaufgabe a

$\overline{BE}=\overline{BC}-\overline{EC}$

Berechne zunächst $\overline{EC}$ und verwende hierfür den Strahlensatz.

$\dfrac{\overline{EC}}{\overline{BC}}=\dfrac{\overline{DE}}{\overline{AB}}$

$\dfrac{\overline{EC}}{5\;\textrm{cm}}=\dfrac{3{,}6\;\textrm{cm}}{7\;\textrm{cm}}$

$\overline{EC}=2{,}57\;\textrm{cm}$

$\overline{BE}=5\;\textrm{cm}-2{,}57\;\textrm{cm}=2{,}43\;\textrm{cm}$

Lösung Teilaufgabe b

$d$ ist der Abstand der Strecken [AB] und [DE].

Dann gilt:

$\cos\left(\sphericalangle CBA-90°\right)= \dfrac{d}{\overline{BE}}$

Um den Winkel $\sphericalangle CBA$ zu bestimmen, berechne zunächst den Winkel $\sphericalangle BAC$. Wende hierzu den Sinussatz auf das Dreieck $ACB$ an.

$$

$\dfrac{\sin( \sphericalangle BAC)}{\overline{BC}}=\dfrac{\sin40°}{7\;\textrm{cm}}$

$\dfrac{\sin( \sphericalangle BAC)}{\overline{5\;\textrm{cm}}}=\dfrac{\sin40°}{7\;\textrm{cm}}$

$\sin( \sphericalangle BAC)=\dfrac{\sin40°\cdot 5\;\textrm{cm}}{7\;\textrm{cm}}=\dfrac{3{,}2139\;\textrm{cm}}{7\;\textrm{cm}}=0{,}4591$$$

$\sphericalangle BAC=\sin^{-1}(0{,}4591)=27{,}33°$

Da die Winkelsumme im Dreieck $180°$beträgt, ergibt sich

$\sphericalangle CBA=180°-40°-27{,}33°=112{,}67°$

$\cos(112{,}67°-90°)=\dfrac{d}{2{,}43\;\text{cm}}$

$d=\cos(22{,}67°)\cdot 2{,}43\;\text{cm}=2{,}24\;\text{cm}$

Der Abstand $d$ der Strecken $[AB]$ und $[DE]$ beträgt $2{,}24\;\text{cm}$.