Das bei rechtwinklige Dreieck ist die Grundfläche der Pyramide mit der Spitze . Der Punkt ist der Fußpunkt der Pyramidenhöhe , die senkrecht auf der Grundfläche steht.
Es gilt:
Die untenstehende Zeichnung zeigt ein Schrägbild der Pyramide . In der Zeichnung gilt: liegt auf der Schrägbildachse.
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
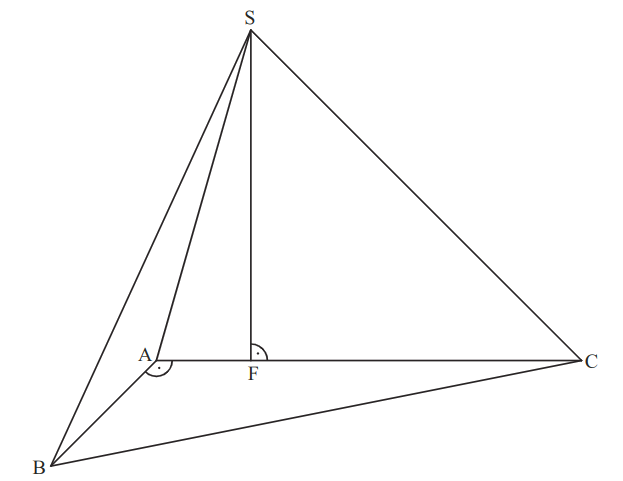
Berechnen Sie das Maß des Winkels .
[Ergebnis: ]
Punkte liegen auf der Strecke . Die Winkel haben das Maß mit . Das Dreieck ist die Grundfläche der Pyramiden mit den Spitzen und den Höhen . Zeichnen Sie die Pyramide sowie deren Höhe für in das Schrägbild zur Aufgabenstellung ein.
Begründen Sie die obere Intervallgrenze für .
Zeigen Sie, dass für die Länge der Strecken in Abhängigkeit von gilt:
.
Berechnen Sie das Volumen der Pyramiden in Abhängigkeit von .







