Die Raute hat die Diagonalenlängen und . Für die Seitenlängen gilt:
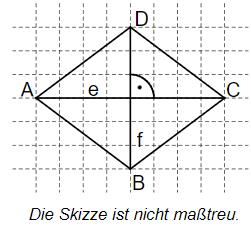
Gib den Flächeninhalt der Raute an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Die Raute hat die Diagonalenlängen und . Für die Seitenlängen gilt:

Gib den Flächeninhalt der Raute an.