2023

Die Aufgabestellung findest du hier als PDF.

1
Berechne
1. $\dfrac{2}{3}+\dfrac{1}{6}=$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche addieren
  Der Hauptnenner ist $6$ .
  $\dfrac{2}{3}=\dfrac{4}{6}$
  $\dfrac{4}{6}+\dfrac{1}{6}=\dfrac{5}{6}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  ermittle zunächst den Hauptnenner
2. $8{,}4\cdot 0{,}1=$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Multiplikation von Dezimalzahlen
  Dazu verschieben wir das Komma der ersten Zahl um 1 nach rechts, der zweiten Zahl um 1 nach rechts und berechnen
  $84\cdot 1=84$
  Anschließend müssen wir das Komma im Ergebnis noch setzen.
  In diesem Fall haben wir
  1+1=2 Nachkommastellen.
  Damit ist $8{,}4\cdot 0{,}1=0{,}84$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Wir multiplizieren die beiden Zahlen zunächst ohne Komma.
3. $1{,}5-0{,}5\cdot 3=$
  
  Beachte die Regel "Punkt vor Strich".
  $1{,}5-0{,}5\cdot 3=1{,}5-1{,}5=0$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $- (2 - 4) + 3 =$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Klammern auflösen
  $- (2 - 4) + 3 = - 2 + 4 + 3 = 5$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte die Vorzeichen beim Auflösen der Klammer.
2
Eine Figur wurde aus gleichartigen Spielsteinen gelegt, die sich nur in der Farbe unterscheiden. Gib in Prozent an, welcher Anteil der Figur aus dunklen Spielsteinen besteht.

Die Figur besteht aus $10\cdot 5=50$ Kästchen.
Sie besteht aus 25 hellen und 25 dunklen Kästchen.
$50 \mathop{\widehat{=}} 100$ %
Dividiere durch 2.
$=> 25 \mathop{\widehat{=}} 50$ %
Der Anteil der dunklen Spielsteine beträgt $50$ %.
3
Mila hat schon 8 neue Englischvokabeln gelernt. Das sind 25% aller Vokabeln, die sie für die nächste Englischstunde zu lernen hat. Gib an, wie viele Vokabeln sie noch lernen muss.

$\displaystyle 8$ $≘$ $\displaystyle 25\ \%$
↓
Multipliziere mit 4.
$\displaystyle 32$ $=$ $\displaystyle 100\ \%$
Mila hat bereits 8 Vokabeln gelernt:
$32 - 8 = 24$
Mila muss insgesamt $32$ Vokabeln lernen. Da sie schon $8$ Vokabeln gelernt hat, muss sie noch $24$ Vokabeln lernen.
Berechne, wie viele Vokabeln $100~\%$ entsprechen.
Ziehe die Vokabeln ab, die Mila schon gelernt hat.
4
Setze bei den beiden Faktoren jeweils ein Komma, so dass eine wahre Aussage entsteht.
$4001 \cdot 5002 = 20013{,}002$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Multiplikation von Dezimalzahlen
Bei einem Produkt von Dezimalzahlen ergibt sich die Anzahl der Kommastellen des Ergebnisses aus der Summe der Kommastellen der beiden Faktoren.
$20013,002$ hat drei Kommastellen.
Beispiele für eine mögliche Lösung sind
$4{,}001 \cdot 5002 = 20013{,}002$
$40{,}01 \cdot 500{,}2 = 20013{,}002$
$400{,}1 \cdot 50{,}02 = 20013{,}002$
Zähle die Anzahl der Kommastellen des Ergebnisses
5
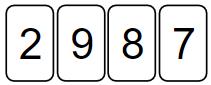
Die abgebildeten Ziffernkärtchen stehen jeweils einmal zur Verfügung. Wähle vier dieser Kärtchen aus und bilde damit die Zahl, deren Wert so nah wie möglich bei 3000 liegt.

Die gesuchte Zahl ist
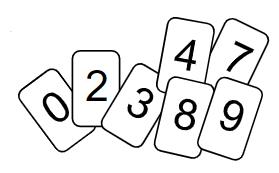
6
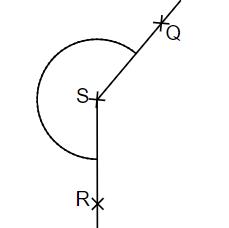
Für das Maß $α$ des Winkels $Q S R$ gilt: $α = 220 °$ . Ergänze den zweiten Schenkel des Winkels und kennzeichne diesen Winkel mit einem Bogen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel
Ein $220$ ° Winkel ist ein überstumpfer Winkel, d.h. $220 ° = 180 ° + 40 °$
Lege das Geodreieck am Scheitelpunkt $S$ des Winkels $\alpha$ an und markiere zunächst den 180° Winkel. Drehe nun das Geodreieck um weitere 40° weiter und zeichne mit der Unterkante des Geodreiecks den gesuchten Schenkel.
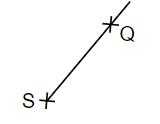
7
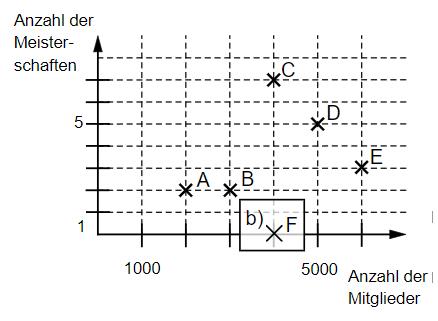
Im abgebildeten Diagramm sind jeweils die Mitgliederzahl und die Anzahl der gewonnenen Meisterschaftenvon fünf Handballvereinen dargestellt.
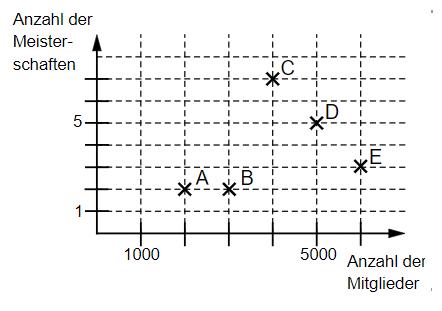
1. Eine Aussage zum Diagramm ist falsch. Kreuze diese an.
  Die Vereine A und B haben die gleiche Anzahl an Mitgliedern.
  Alle Vereine haben zusammen 19 Meisterschaften gewonnen.
  Verein D hat mehr als doppelt so viele Mitglieder wie Verein A.
  Die Vereine A, B, D und E haben zusammen 5 Meisterschaften mehr gewonnen als Verein C.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Aus dem Diagramm kannst du folgendes ablesen.
  Verein $A$ hat $2000$ Mitglieder und Verein $B$ hat $3000$ Mitglieder.
  Alle Vereine zusammen haben $2 + 2 + 7 + 5 + 3 = 19$ Meisterschaften gewonnen.
  Verein $D$ hat $5000$ Mitglieder, also mehr als doppelt so viele wie Verein $A .$
  Die Vereine $A, B, D$ und $E$ haben zusammen $2 + 2 + 5 + 3 = 12$ Meisterschaften und Verein $C$ hat $7$ Meisterschaften gewonnen. $12 - 7 = 5$ .
  $= >$ Die Vereine $A, B, D$ und $E$ haben zusammen $5$ Meisterschaften mehr gewonnen als Verein $C$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Der Verein F hat noch nie eine Meisterschaft gewonnen und halb so viele Mitglieder wie die Vereine A und E zusammen. Trage das Kreuz für den Verein F in das Diagramm ein.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8
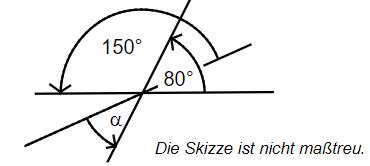
Drei Geraden schneiden sich in einem Punkt. Gib das Winkelmaß $α$ an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel
Nebenwinkel: $150 ° + 30 ° = 180 °$
$80 ° - 30 ° = 50 °$
$\alpha$ ist ein Scheitelwinkel zu dem $50 °$ Winkel.
$\Rightarrow \alpha=50°$
9
Gib einen Bruch mit dem Wert $0,25$ an, der aus einem einstelligen Zähler und einem zweistelligen Nenner besteht.
$0{,}25=\dfrac{\square}{\square}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
$0{,}25=\dfrac{1}{4}$
Beispiele:
Erweitern mit 3: $\dfrac{1}{4}=\dfrac{1\cdot 3}{4\cdot 3}=\dfrac{3}{12}$
Erweitern mit 4: $\dfrac{1}{4}=\dfrac{1\cdot 4}{4\cdot 4}=\dfrac{4}{16}$
Schreibe $0,25$ als Bruch und erweitere diesen Bruch.
10
Erkan hat das Dreieck $S T U$ mit $|\overline{ST}|= 4cm$ gezeichnet. Stefan soll mit der bereits vorgegebenen Seite $\overline{PQ}$ mit $|\overline{PQ}|= 4 cm$ ein Dreieck $P Q R$ zeichnen, so dass gilt:
- Beide Dreiecke haben den gleichen Flächeninhalt A.
- Stefans Dreieck ist gleichschenklig mit der Basis $\overline{PQ}$ .
Zeichne die fehlenden Schenkel des Dreiecks $P Q R$ ein.

Fläche Parallelogramm: $A_{Parallelogramm}= g\cdot h$
Fläche Dreieck: $A_{Dreieck}=\dfrac{1}{2}\cdot g\cdot h$
Das linke Dreieck ist ein halbes Parallelogramm mit $g = 4 c m$ und $h = 2 c m$
$A_{STU}=\dfrac{1}{2}\cdot 4\cdot 2=4$
Das rechte Dreieck ist gleichschenklig und hat $g = 4 c m$ und $h = 2 c m$ .
$A_{PQR}=\dfrac{1}{2}\cdot 4\cdot 2=4$
Beide Dreiecke haben die Fläche $4 c m^{2}$ .
11
Welche der folgenden fünf Zahlen ist die kleinste Zahl, die gerundet $0,73$ ergibt? Kreuze an.
0,7252
$0,7248$
0,7349
0,7350
0,7007
Für diese Aufgabe benötigst Du folgendes Grundwissen: Runden
Wenn diese Stelle eine 0,1,2,3 oder 4 ist, wird abgerundet.
Wenn diese Stelle eine 5,6,7,8 oder 9 ist, wird aufgerundet.
$0,7252$ wird auf $0,73$ aufgerundet und ist die kleinste der angegebenen Zahlen, die gerundet $0,73$ ergibt.
Wenn auf Hunderstel gerundet wird, musst du die 3. Stelle hinter dem Komma betrachten.
12
Ein quaderförmiger Karton hat folgende Innenmaße: Länge $l = 9\ cm$ , Breite $b = 6\ cm$ und Höhe $h = 7\ cm$ . In diesen Karton werden $12$ Würfel mit der Kantenlänge $a = 3\ cm$ in zwei Schichten aufeinandergestapelt (siehe Skizze).
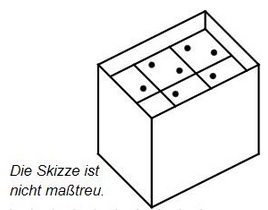
Da die Würfel den Karton nicht bis oben hin ausfüllen, soll das restliche Volumen $V$ zum Transport mit Füllmaterial ausgestopft werden. Gib an, wie groß das restliche Volumen $V$ ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quader
$L_{\text{Quader}}=l\cdot b\cdot h$
$L_{\text{Karton}}=\mathrm{9\ cm\cdot 6\ cm\cdot 7\ cm=378\ cm^3}$
$L_{\text{Würfel}}=\mathrm{3\ cm\cdot 3\ cm\cdot 3\ cm=27\ cm^3}$
Gesamtvolumen der $12$ Würfel: $\mathrm{27\ cm^3\cdot 12=324\ cm^3}$
$\mathrm{378\ cm^3-324\ cm^3=54\ cm^3}$
Das restliche Volumen $V$ beträgt $\mathrm{54\ cm^3}$ .
Alternative:
Du kannst auch so rechnen:
In eine Schicht passen $6$ Würfel, da die Länge des Kartons $3\cdot3\text{ cm}=9\text{ cm}$ und Breite $2\cdot 3\text{ cm}=6\text{ cm}$ beträgt.
Zwei Schichten Würfel sind dann $2\cdot 3\text{ cm} =6\text{ cm}$ hoch, es bleibt also noch $7\text{ cm}-6\text{ cm}= 1\text{ cm}$ an Höhe übrig. Das Restvolumen ist dann $V=6\text{ cm} \cdot 9\text{ cm} \cdot\text{ 1 cm} =54\text{ cm}^3$ .
Das restliche Volumen $V$ beträgt $54\text{ cm}^3$ .
13
Die Raute $A B C D$ hat die Diagonalenlängen $e = 8~\text{cm}$ und $f = 6~\text{cm}$ . Für die Seitenlängen gilt:
$a = b = c = d = 5~\text{cm}$
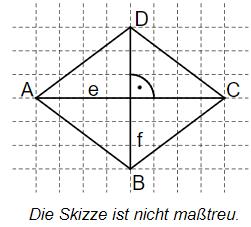
Gib den Flächeninhalt $A$ der Raute $A B C D$ an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Raute
$A_{\text{Raute}}=\frac12\cdot e\cdot f$
$A_{\text{Raute}}=\dfrac{1}{2}\cdot 8\text{ cm}\cdot 6\text{ cm}=24\text{ cm}^2$
Der Flächeninhalt der Raute beträgt $24~\text{cm}^2$ .
14
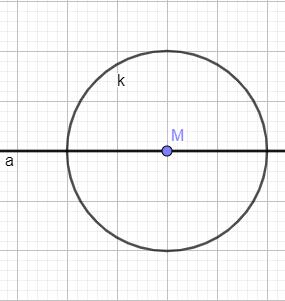
Ein Kreis $k$ mit dem Radius $r = 2~\text{cm}$ soll durch Achsenspiegelung an der Achse $a$ auf sich selbst abgebildet werden. Zeichne einen möglichen Mittelpunkt $M$ eines solchen Kreises ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Achsenspiegelung
Wenn der Kreis durch Achsenspiegelung an der Achse $a$ auf sich selbst abgebildet werden soll, dann muss der Kreismittelpunkt $M$ auf der Spiegelachse $a$ liegen.
15
Die Abbildung zeigt maßstabsgetreu eine Autobahnbrücke mit sechs Pfeilern. Der längste Pfeiler ist nur $60~\text{m}$ kürzer als der Eiffelturm, der $330~\text{m}$ hoch ist. Wie lang ist die Brücke?
Gib deinen Lösungsweg an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Maßstab
Länge des längsten Pfeilers: $3 c m$ ;
$3cm \mathop{\widehat{=}} 330m-60m=270m$
$3cm \mathop{\widehat{=}} 270m$
Länge der Brücke: $9 c m$ ;
$9cm \mathop{\widehat{=}} 3\cdot 270m=810m.$
$9cm \mathop{\widehat{=}}810m$
Die Brücke ist $810 m$ lang.
Vergleiche die in der Zeichnung gemessenen Längen mit der Realität.
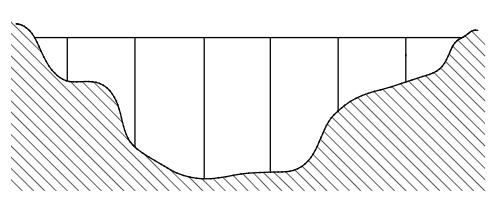
16
Mia wünscht sich ein rechteckiges Freigehege für ihre Hühner mit einem Flächeninhalt von mindestens $40~\text{m²}$ . Ihr Vater zeigt ihr einen Plan, bei dem der Zaun wie in der Skizze dargestellt an die $5~\text{m}$ lange Wand des Hühnerstalls anschließt. Für die fehlenden 3 Seiten des Geheges sollen insgesamt $19~\text{m}$ Zaun vollständig verbaut werden.
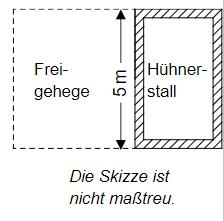
Begründe rechnerisch, dass Mias Wunsch nach einem Gehege mit mindestens $40\text{ m²}$ Flächeninhalt nicht erfüllt werden kann.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
$U_\mathrm{\text{Rechteck}}=2\cdot l+2\cdot b$
Der Gesamtumfang des Rechtecks beträgt $19\text{ m}+5 \text{ m}=24\text{ m}.$
Somit ergibt sich für die Breite des Rechtecks $(24\text{ m}-2\cdot 5\text{ m}):2=14\text{ m}:2=7\text{ m}$
$A_{\text{Rechteck}}=l\cdot b$
$A_{\text{Rechteck}}=5\text{ m}\cdot 7\text{ m}=35\text{ m}^2<40\text{ m}^2$

Gib die Lösungsmenge L der folgenden Gleichung an $(\mathbb{G}=\mathbb{Q}).$

$–3 \cdot x = –10 – 2$

L={_____}

18
Gegeben ist der Term $T (x) = 2 x – 1$ $(\mathbb{G}=\mathbb{Q})$ . Kreuze an, welche Wertepaare zu diesem Term gehören.
$x = - 1; T (x) = 0$
$x = 0; T (x) = 1$
$x = 2; T (x) = 2$
$x = - 1; T (x) = - 3$
$x = 0; T (x) = 0$
$x = 2; T (x) = 3$
$x = - 1; T (x) = - 3$
$x = 0; T (x) = - 1$
$x = 2; T (x) = 3$
$x = - 1; T (x) = - 3$
$x = 0; T (x) = - 1$
$x = 2; T (x) = 1$
$x=-1 \Rightarrow T(-1)=-3 \neq0$
$x=0 \Rightarrow T0)=-1 \neq1$
$x=2 \Rightarrow T(2)=3 \neq2$
$\Rightarrow$ Diese Wertepaare gehören nicht zu dem Term $T (x) = 2 x - 1$
$x=-1 \Rightarrow T(-1)=-3$
$x=0 \Rightarrow T(0)=-1 \neq0$
$x=2 \Rightarrow T(2)=3$
$\Rightarrow$ Diese Wertepaare gehören nicht zu dem Term $T (x) = 2 x - 1$
$x=-1 \Rightarrow T(-1)=-3$
$x=0 \Rightarrow T0)=-1$
x $=2 \Rightarrow T(2)=3$
$\Rightarrow$ Alle Werte stimmen mit den angegeben Wertepaaren überein.
$x=-1 \Rightarrow T(-1)=-3$
$x=0 \Rightarrow T(0)=-1$
$x=2 \Rightarrow T(2)=3 \neq1$
$\Rightarrow$ Diese Wertepaare gehören nicht zu dem Term $T (x) = 2 x - 1$ .
Setze $x$ in den Term ein und bereche $T (x) .$
19
Von einem $7{,}1~\text{cm}$ dicken Holzbrett werden mit einer Hobelmaschine $6~\text{mm}$ abgehobelt. Gib an, wie dick das Brett danach ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Längeneinheiten
$7{,}1~\text{cm}=71~\text{mm}$
$71~\text{mm}-6~\text{mm}=65~\text{mm}$
Das Brett ist $65~\text{mm}$ oder $6{,}5~\text{cm}$ dick.
Rechne in mm um.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle -3\cdot x$	$=$	$\displaystyle -10-2$
	↓	fasse zusammen
$\displaystyle -3\cdot x$	$=$	$\displaystyle -12$	$\displaystyle :\left(-3\right)$
	↓	dividiere
$\displaystyle x$	$=$	$\displaystyle 4$
	↓	multipiliziere

$\displaystyle 8$	$≘$	$\displaystyle 25\ \%$
	↓	Multipliziere mit 4.
$\displaystyle 32$	$=$	$\displaystyle 100\ \%$

2023

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?