Teil 1 Stochastik

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellungen zum Ausdrucken findest du hier als PDF.

Die Aufgaben im ersten Teil der Abschlussprüfung sind ohne Hilfsmittel (Taschenrechner, Merkhilfe oder Formelsammlung, Tafelwerk) zu lösen.

Versuch es also nur mit Blatt und Stift.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
A und B sind vereinbare Ereignisse des Ergebnisraums $\Omega$ . (3 BE)
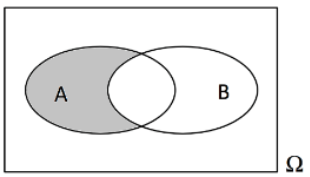
1. Geben Sie das im nebenstehenden Venn-Diagramm grau markierte Ereignis $E_1$ möglichst einfach als Verknüpfung der Ereignisse A und B an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Venn-Diagramm
  Der Kreis mit der Beschriftung A ist ausgemalt, aber nicht komplett: Der Bereich, indem A und B sich schneiden, ist ausgespart. Es soll also A erfüllt sein, aber B nicht:
  $E_1=A\cap\overline B$ oder $E_1=A\backslash B$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überlege dir, was für Elemente der Menge zutreffen soll und was nicht.
2. Veranschaulichen Sie das Ereignis $E_2=A\cup \overline B$ in einem Venn-Diagramm.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Venn-Diagramm
  Da bei Vereinigungen entweder die linke Seite oder die rechte Seite oder beide Seiten zutreffen dürfen, darfst du alles ausmalen, bei dem mindestens eins zutrifft.
  Male zuerst A an:
  Male nun zusätzlich $\overline B$ an, wobei $\overline B$ alles außer dem Kreis B ist:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Um Vereinigungen $\cup$ zu malen, kannst du jedes Element nacheinander komplett ausmalen.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Ein Handballspieler trainiert Siebenmeter-Würfe, wobei der Torhüter seines Vereins im Tor steht.
Erfahrungsgemäß trifft er bei 80% seiner Würfe ins Tor.
1. Der Spieler führt zwei Siebenmeter-Würfe aus.
  Berechnen Sie jeweils die Wahrscheinlichkeit folgender Ereignisse:
  $E_3:$ "Der Spieler trifft jedes Mal."
  $E_4:$ "Der Spieler trifft mindestens einmal."
  (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pfadregeln
  Wahrscheinlichkeit von $E_3$
  Da der Spieler mit einer Wahrscheinlichkeit von 80% trifft und zweimal wirft, ergibt sich mit der Pfadregel:
  $P(E_3)=0{,}8^2=0{,}8\cdot0{,}8=0{,}64$
  Die Wahrscheinlichkeit, dass er zweimal trifft, beträgt deshalb 64%
  Wahrscheinlichkeit von $E_4$
  Wenn der Spieler mindestens einmal trifft, bedeutet dass ausführlich: Er trifft entweder nur beim ersten Mal oder nur beim zweiten Mal oder beide Male.
  Es ist hier leichter mit dem Gegenereignis zu rechnen und von 100% die Wahrscheinlichkeit abzuziehen, dass er beide Würfe verfehlt.
  Die Wahrscheinlichkeit für einen verfehlten Wurf ist dabei 20%:
  $P(E_4)=1-0{,}2^2=1-0{,}04=0{,}96$
  Mit einer Wahrscheinlichkeit von 96% trifft er also mindestens einmal.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bei diesem sehr kleinen Bernoulli-Experiment kannst du dir auch mit einem kleinen Baumdiagramm helfen. Anschließend verwendest du die Pfadregeln.
2. Formulieren Sie zwei Ereignisse $E_5$ und $E_6$ im Sachzusammenhang, deren Wahrscheinlichkeiten sich wie folgt berechnen lassen:
  $P(E_5)=0{,}8^{20}$
  $P(E_6)=\binom{50}{30}\cdot0{,}8^{30}\cdot0{,}2^{20}$
  (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bernoulli-Kette
  Ereignis $E_5$
  Aus der Angabe weißt du, dass $80\%=0{,}8$ die Wahrscheinlichkeit dafür ist, dass das Tor getroffen wird.
  Der Exponent gibt an, wie oft dieses Ergebnis eintritt.
  Insgesamt ist das Ereignis $E_5$ , dass der Spieler bei 20 Würfen 20 Treffer erzielt.
  Ereignis $E_6$
  Hier siehst du die klassische Bernoulli-Formel. Da $0{,}8^{30}$ berechnet wird, trifft der Spieler diesmal 30 Mal. Durch den Binomialkoeffizient $\binom{50}{30}$ kannst du erkennen, dass er von 50 Würfen genau 30 Würfe trifft, die Position der Würfe aber nicht relevant ist.
  Kurz: $E_6$ ist das Ereignis, dass der Spieler bei 50 Würfen genau 30 Würfe trifft.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Achte bei der Struktur der Terme auf folgende Punkte:
  Was ist die Bedeutung hinter den Exponenten?
  Was bedeutet 0,8 bzw 0,2 in dieser Situation?
  Bei welchen Aufgaben verwendest du den Binomialkoeffizienten $\binom n k$ ?

Einer Gruppe von fünf Jugendlichen werden zwei Freikarten für ein Rockkonzert zur Verfügung gestellt. Um diese zu verteilen, werden nacheinander Lose gezogen, ohne diese zurückzulegen. Jeder Jugendliche zieht dabei genau einmal. Neben den zwei Gewinnlosen für die Freikarten befinden sich drei Nieten in der Lostrommel.

Entscheiden Sie unter Zuhilfenahme einer geeigneten Rechnung, ob der Zweite, der zieht, die gleiche Chance auf eine Freikarte hat wie der Erste. (4 BE)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Laut der 2. Pfadregel addierst du die Wahrscheinlichkeiten der einzelnen Pfade.
	↓
$\displaystyle P(\text{"zweite Person gewinnt"})$	$=$	$\displaystyle P(E_1)+P(E_2)$
	↓	Verwende die 1. Pfadregel
	$=$	$\displaystyle \frac{2}{5}\cdot\frac{1}{4}+\frac{3}{5}\cdot\frac{2}{4}$
	$=$	$\displaystyle 0{,}1+0{,}3$
	$=$	$\displaystyle 0{,}4$

Teil 1 Stochastik

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit von $E_3$

Wahrscheinlichkeit von $E_4$

Hast du eine Frage oder Feedback?

Ereignis $E_5$

Ereignis $E_6$

Hast du eine Frage oder Feedback?

Gewinnwahrscheinlichkeit der ersten Person

Gewinnwahrscheinlichkeit der zweiten Person

Fazit

Teil 1 Stochastik

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Wahrscheinlichkeit von E3E_3E3​

Wahrscheinlichkeit von E4E_4E4​

Hast du eine Frage oder Feedback?

Ereignis E5E_5E5​

Ereignis E6E_6E6​

Hast du eine Frage oder Feedback?

Gewinnwahrscheinlichkeit der ersten Person

Gewinnwahrscheinlichkeit der zweiten Person

Fazit

Wahrscheinlichkeit von $E_3$

Wahrscheinlichkeit von $E_4$

Ereignis $E_5$

Ereignis $E_6$