Venn-Diagramm

Venn-Diagramme werden in der Mengenlehre und Wahrscheinlichkeitsrechnung dazu verwendet, Zusammenhänge zwischen zwei Mengen oder Ereignissen grafisch darzustellen. Wenn man tatsächliche Werte von Mengen oder Wahrscheinlichkeiten von Ereignissen darstellen will, verwendet man eher Balkendiagramme oder Kreisdiagramme.

Aufbau

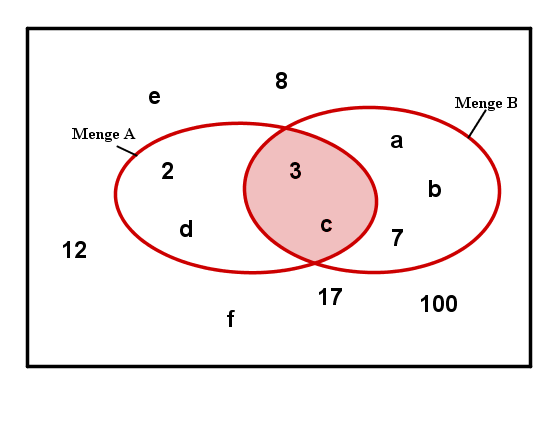
Ein Venn-Diagramm besteht aus einem Rechteck, das sinnbildlich für den Raum aller Mengen oder den Ereignisraum steht (man sagt auch das gesamte Universum) und Kreisen, die für die einzelnen Mengen oder Ergebnisse stehen. Jedes Element (durch einen Punkt veranschaulicht), das innerhalb eines Kreises liegt, liegt dann in den Mengen, die die Kreise darstellen.

Beispiel

Gegeben sind die Mengen $A$ und $B$ mit

$A=\left\{2{,}3,\mathrm c,\mathrm d\right\}$

$B=\left\{3{,}7,\mathrm a,\mathrm b,\mathrm c\right\}$

Dann ist $A\cap B=\left\{3,\mathrm c\right\}$ die Schnittmenge von $A$ und $B$ .

Die nebenstehende Abbildung veranschaulicht das Beispiel mithilfe eines Venn-Diagramms.

Da man normalerweise Kreise gleicher Größe verwendet, kann man keine Aussagen über die Mächtigkeit der einzelnen Mengen oder die Wahrscheinlichkeit der einzelnen Ereignisse machen. Es kann auch sein, dass dargestellte Mengen oder Schnittmengen leer sind.

Man kann beliebig viele Mengen in einem Venn-Diagramm darstellen. Solange man aber echte Kreise verwendet, bekommt man Probleme, alle möglichen Schnittmengen der Mengen darzustellen.

Beispiele von Venn-Diagrammen zweier Mengen A und B

Hier folgen ein paar wichtige Mengen, im Venn-Diagramm rot markiert.

Die Leere Menge $\emptyset$ , enthält keine Elemente.

Alle Elemente von $A$ werden rot markiert.

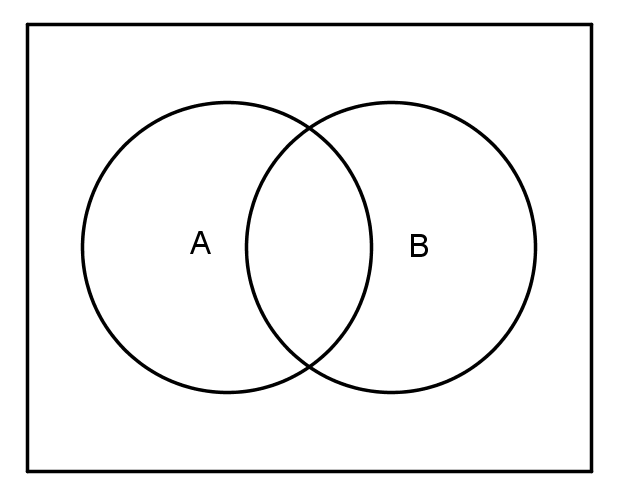
Der Ereignisraum $\Omega$ enthält alle Elemente.

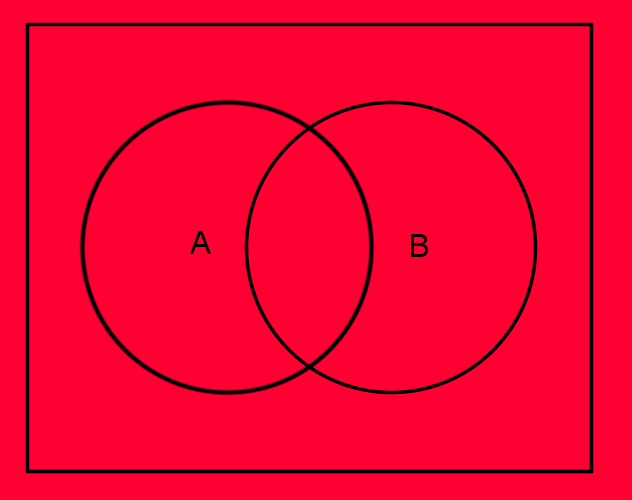
Das Komplement von $A$ geschnitten $B$ , also $\overline{A\cap B}$ , enthält alle Elemente, die nicht in $A$ und $B$ liegen.

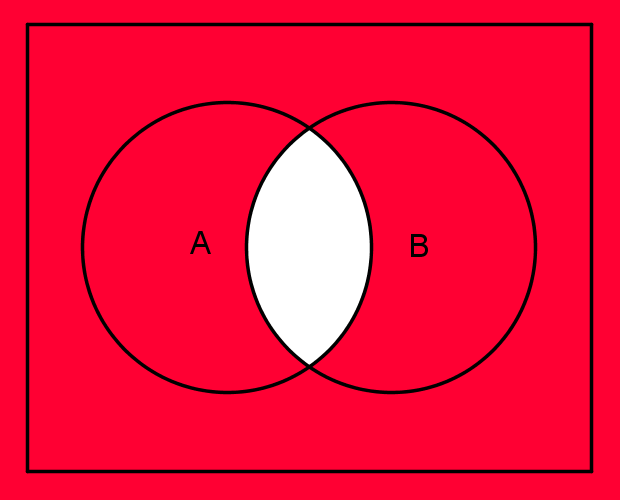
Das Komplement von $A$ vereinigt $B$ , also $\overline{A\cup B}$ , enthält alle Elemente, die nicht in $A$ oder $B$ liegen.

$A$ ohne $B$ , also $A\setminus B$ , enthält alle Elemente von $A$ , die nicht in $B$ liegen.

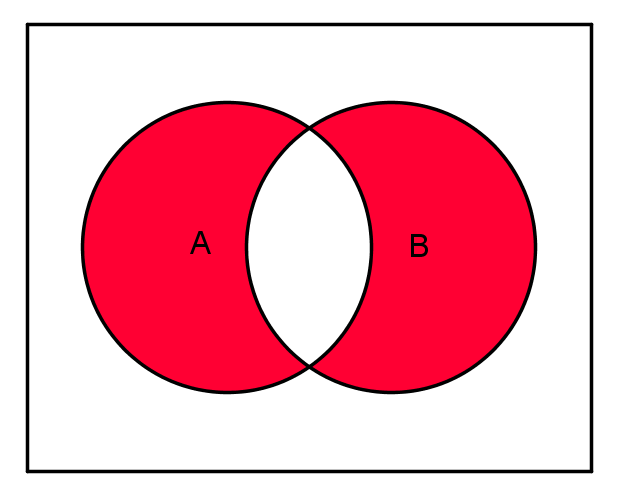
Die symmetrische Differenz $A\Delta B$ enthält alle Elemente, die nur in $A$ oder nur in $B$ liegen, aber nicht in $A$ und $B$ .

Hier findest du Aufgaben zu Venn-Diagrammen.

Übungsaufgaben: Venn-Diagramm

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Venn-Diagramm

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?