Mathe Prüfungsaufgaben mit Lösungen

Wahlaufgabe 1 - Körperberechnung

Die Abbildung zeigt einen kugelförmigen Gasspeicher in Braunschweig. Er hat den Außendurchmesser $d = 27 ~\text{m}$ .

Berechne die Oberfläche des kugelförmigen Gasspeichers. (2 BE)

Der Pfeil zeigt auf einen Ring, der kreisförmig um die Mitte des Gasspeichers verläuft. Der Ring ist $90 ~\text{m}$ lang.

Berechne den Abstand zwischen dem Gasspeicher und dem Ring. (3 BE)

Für Reparaturarbeiten am Gasspeicher wird ein Kran aufgestellt. (2 BE)

Berechne die Länge der Strecke x.

Die Metallwand des Gasspeichers ist $0{,}03 ~\text{m}$ dick.

Berechne das innere Volumen des Gasspeichers. (2 BE)

Der Radius eines anderen kugelförmigen Gasspeichers ist $\sqrt[3]{2}$ - mal so groß wie der Radius des Gasspeichers in Braunschweig.

Zeige mithilfe einer Rechnung, dass das Volumen dieses Gasspeichers doppelt so groß ist. (1 BE)

2

Wahlaufgabe 2 - Wahrscheinlichkeit

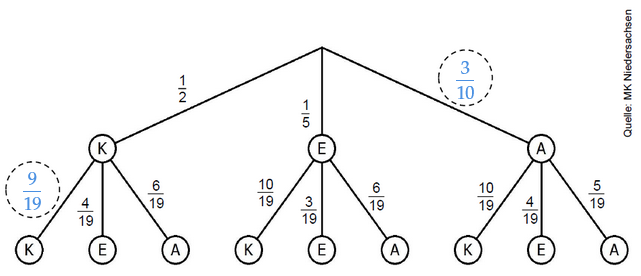
Pia und Lea trinken gerne Tee. Diese Teebeutel liegen unsortiert in einer Teebox:

10 Beutel Kamillentee (K)
4 Beutel Erdbeertee (E)
6 Beutel Apfeltee (A).

Pia greift ohne hinzusehen in die Teebox und zieht nacheinander zwei Teebeutel heraus.
Ergänze im Baumdiagramm die fehlenden Wahrscheinlichkeiten. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
In der ersten Stufe muss die Wahrscheinlichkeit:
betragen.
In der zweiten Stufe muss die Wahrscheinlichkeit:
betragen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Verwende die Knotenregel. Die Wahrscheinlichkeiten aller Äste aus einem Knoten müssen zusammen $1$ ergeben.
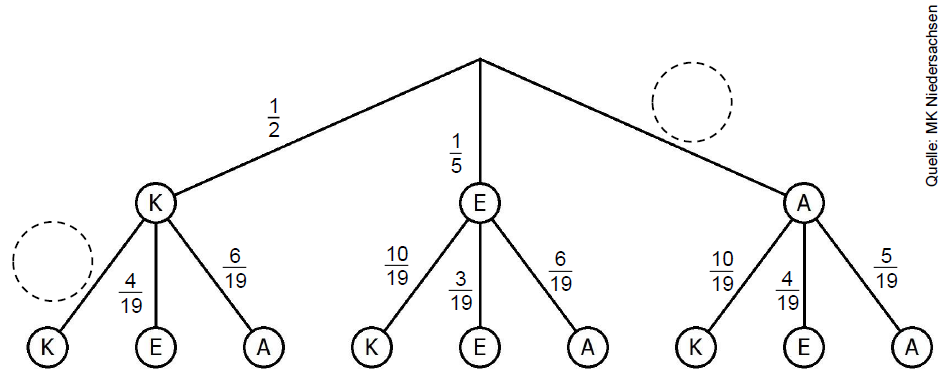
Berechne die Wahrscheinlichkeit, dass Pia erst Kamillentee und dann Apfeltee zieht.
(2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Pfadregeln
Die Wahrscheinlichkeit für Kamillentee ist:
$P(K)=\dfrac12$
Im zweiten Zug Apfeltee zu ziehen, kann man im Baumdiagramm auslesen:
$P(A)=\dfrac{6}{19}$
Insgesamt werden die Wahrscheinlichkeiten multipliziert:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Wahrscheinlichkeit, indem du die einzelnen Wahrscheinlichkeiten entlang eines Pfades multiplizierst.

Pia und Lea mögen keinen Erdbeertee.

Berechne die Wahrscheinlichkeit, dass Pia keinen Erdbeertee zieht. (3 BE)

Lea berechnet die Wahrscheinlichkeit für ein Ereignis mit der folgenden Rechnung:
Gib das passende Ereignis an. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gegenereignis
Die Wahrscheinlichkeit stellt folgendes Ereignis dar:
Lea zieht keinen Kamillen- und Erdbeertee.
$P=1-\left(\underbrace{\dfrac{1}{2}\cdot \dfrac{4}{19}}_{\text{P(KE)}}+\underbrace{\dfrac{1}{5}\cdot \dfrac{10}{19}}_{\text{P(EK)}}\right)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der Term stellt ein Gegenereignis dar.
Die einzelnen Terme können im Baumdiagramme mit Teesorten abgeglichen werden.
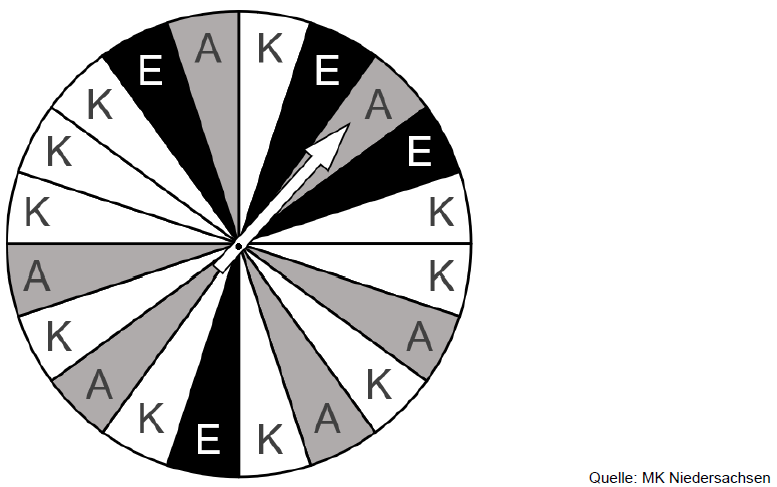
Pia und Lea wollen mit dem abgebildeten Glücksrad entscheiden, welchen Tee sie als nächstes trinken. Sie drehen das Glücksrad zweimal.
Begründe, dass das Zufallsexperiment nicht zum Baumdiagramm aus Aufgabenteil a) passt. (1 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Urnenmodell
Beim Ziehen aus der Teebox verändern sich die Wahrscheinlichkeit innerhalb der Stufen.
Beim Drehen am Glücksrad verändert sich die Wahrscheinlichkeit nicht zwischen den Stufen.
$\rightarrow$ Wenn sie das Glücksrad zweimal drehen, kann das Zufallsexperiment nicht gleich sein.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Vergleiche beide Zufallsexperimente:
Beim Ziehen aus der Teebox - wird zurückgelegt oder nicht?
Beim Drehen am Glücksrad - bleiben die Felder gleich oder nicht?

3

Wahlaufgabe 3 - Trigonometrie

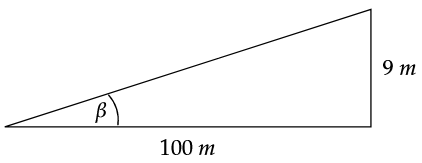
Eine Bergbahn im Harz fährt von einer Talstation zu einer Bergstation. Danny hat eine Skizze gezeichnet und einige Streckenlängen eingetragen.

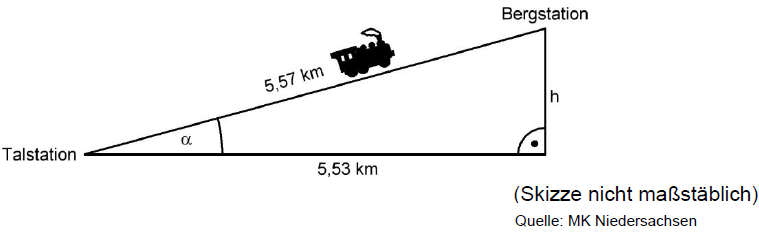
Berechne den Höhenunterschied $h$ . (2 BE)

Danny hat den Steigungswinkel $\alpha$ der Bergbahn berechnet. Sein Ergebnis für $\alpha$ ist ungefähr $7°$ .

Bestätige mithilfe einer Rechnung, dass Dannys Ergebnis richtig ist. (2 BE)

Eine Bergbahn in den Alpen hat eine Steigung von 9 %. (3 BE)

Entscheide mithilfe einer Rechnung, welche Bergbahn die größere Steigung hat.

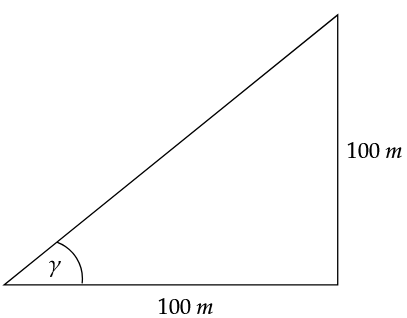
Danny behauptet: „Die Steigung einer Strecke kann höchstens $100 ~\%$ betragen.“
Zeige, dass Dannys Behauptung falsch ist. (1 BE)
Skizze mit $100~\%$ .
$100~\%$ Steigung entspricht dem Aufbau dieser Skizze.
Da dies ein gleichschenkliges Dreieck mit rechtem Winkel ist, beträgt der Winkel $\gamma$ $45°$ .
Definitiv kann der Winkel größer sein als $45°$ . Dannys Behauptung ist falsch.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Welchem rechtwinkligen Dreieck entspricht der Aufgabe mit $100~\%$ Steigung?
Bestimme den Winkel dieses Dreiecks. Kann der Winkel noch größer werden?

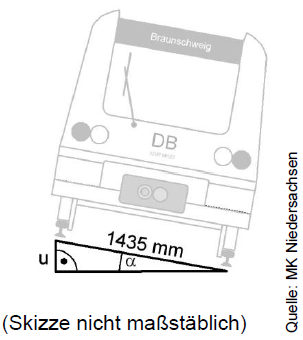
Damit Züge in Kurven schneller fahren können, werden die Gleise etwas geneigt. Die maximale Geschwindigkeit hängt vom Neigungswinkel $\alpha$ ab.

Bestimme die maximale Geschwindigkeit, mit der ein Zug bei einem Höhenunterschied von $u = 217 ~\text{mm}$ durch die Kurve fahren darf. (2 BE)

4

Wahlaufgabe 4 - Quadratische Funktionen

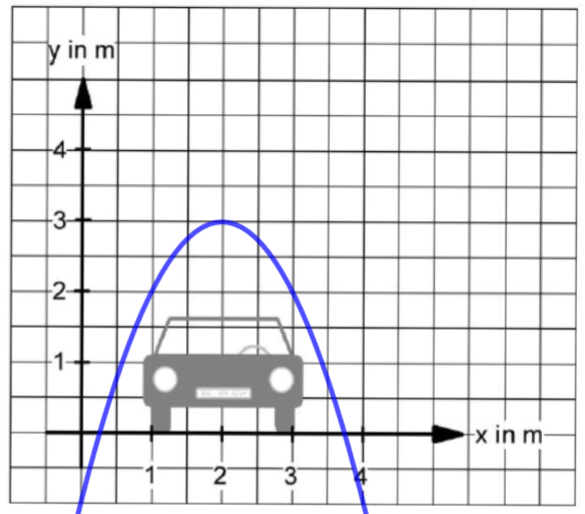
Es wird eine Toreinfahrt in Form einer Parabel gebaut.

Die Parabel hat die Funktionsgleichung $y = – x² + 4x – 1.$

Ergänze den fehlenden Wert in der Wertetabelle. (1 BE)

Skizziere die parabelförmige Toreinfahrt in das Koordinatensystem. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel zeichnen
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Verwende die Wertetabelle aus Aufgabenteil (a) und skizziere die Parabel.
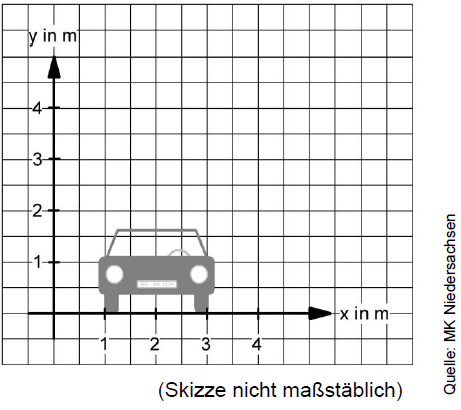
Notiere die Funktionsgleichung in der Scheitelpunktform. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform
Aus der Wertetabelle bzw. der Skizze kann man den Scheitel bestimmen:
Der Öffnungsfaktor der Parabel ist $a=-1$ . Zusammen ergibt sich eingesetzt:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme den Scheitel aus der Wertetabelle bzw. der Skizze oben.
Den Vorfaktor $a$ in der Scheitelform $y=a(x-d)^2+e$ ist der Öffnungsfaktor der Parabel.

Michel hat begonnen, die Breite der Toreinfahrt am Boden zu berechnen.

Vervollständige Michels Rechnung und berechne die Breite der Toreinfahrt am Boden.

(4 BE)

$\displaystyle 0$	$=$	$\displaystyle -x^2+4x-1$	$\displaystyle :\left(-1\right)$
$\displaystyle 0$	$=$	$\displaystyle x^2-4x+1$

Um die Breite der Toreinfahrt am Boden zu berechnen, hat Michel die Gleichung $y = – x² + 4x – 1$ im ersten Schritt folgendermaßen geändert: $0 = – x² + 4x – 1$ .
Begründe Michels ersten Schritt. (1 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: pq-Formel
An den Schnittpunkten des Graphen mit der $x$ -Achse ist der $y$ -Wert $0$ .
Also wird dieser $0$ gesetzt und die Gleichung im Anschluss gelöst.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$\displaystyle O$	$=$	$\displaystyle 4\pi\ r^2$
	↓	Einsetzen
	$=$	$\displaystyle 4\pi\ 13{,}5^2$
	$=$	$\displaystyle 2290{,}221...$
	$≈$	$\displaystyle 2290{,}22\ m^2$

$\displaystyle U$	$=$	$\displaystyle 2\pi r$	$\displaystyle :2\pi$
$\displaystyle r$	$=$	$\displaystyle \frac{U}{2\pi}$
	↓	Einsetzen
	$=$	$\displaystyle \frac{90}{2\pi}$
	$=$	$\displaystyle 14{,}323...$
	$≈$	$\displaystyle 14{,}32\ m$

$\displaystyle x^2+17^2$	$=$	$\displaystyle 19^2$	$\displaystyle -17^2$
$\displaystyle x^2$	$=$	$\displaystyle 19^2-17^2$	$\displaystyle \sqrt{ }$
$\displaystyle x$	$=$	$\displaystyle \sqrt{19^2-17^2}$
	$=$	$\displaystyle 8{,}485...$
	$≈$	$\displaystyle 8{,}49\ m$

$\displaystyle V$	$=$	$\displaystyle \frac{4}{3}\pi\ r^3$
	↓	$r=13{,}5~\text{m}-0{,}03~\text{m}=13{,}47~\text{m}$
	$=$	$\displaystyle \frac{4}{3}\pi\ 13{,}47^3$
	$=$	$\displaystyle 10237{,}440...$
	↓	Runden
	$≈$	$\displaystyle 10237{,}44\ m^3$

$\displaystyle V'$	$=$	$\displaystyle \frac{4}{3}\pi\ r'^3$
	↓	$r'=\sqrt[3]{2}\cdot r$
	$=$	$\displaystyle \frac{4}{3}\pi\ \left(\sqrt[3]{2}\cdot r\right)^3$
	↓	Potenzgesetze
	$=$	$\displaystyle \frac{4}{3}\pi\ \cdot\sqrt[3]{2}^3\cdot r^3$
	$=$	$\displaystyle \frac{4}{3}\pi\ \cdot \color{green}2\color{black}\cdot r^3$

Wahlteil

Wahlaufgabe 1 - Körperberechnung

Hast du eine Frage oder Feedback?

Radius des Ringes

Vergleich der Radien

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Wahlaufgabe 2 - Wahrscheinlichkeit

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösung über das Gegenereignis

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Wahlaufgabe 3 - Trigonometrie

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Wahlaufgabe 4 - Quadratische Funktionen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Nullstellen berechnen

Abstand der Nullstellen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

$\displaystyle P(\text{Erdbeertee})$	$=$	$\displaystyle P(KE)+P(EK)+P(EE)+P(EA)+P(AE)$
	$=$	$\displaystyle \frac{1}{2}\cdot\frac{4}{19}+\frac{1}{5}\cdot\frac{10}{19}+\frac{1}{5}\cdot\frac{3}{19}+\frac{1}{5}\cdot\frac{6}{19}+\frac{3}{10}\cdot\frac{4}{19}$
	$=$	$\displaystyle \frac{4}{38}+\frac{10}{95}+\frac{3}{95}+\frac{6}{95}+\frac{12}{190}$
	$=$	$\displaystyle \frac{70}{190}$

$\displaystyle h^2+5{,}53^2$	$=$	$\displaystyle 5{,}57^2$	$\displaystyle -5{,}53^2$
$\displaystyle h^2$	$=$	$\displaystyle 5{,}57^2-5{,}53^2$	$\displaystyle \sqrt{ }$
$\displaystyle h$	$=$	$\displaystyle \sqrt{5{,}57^2-5{,}53^2}$
	$=$	$\displaystyle 0{,}666...$
	$≈$	$\displaystyle 0{,}67\ km$

$\cos\alpha=\dfrac{\text{Ankathete}}{\text{Hypotenuse}}$
	↓
$\displaystyle \cos\alpha$	$=$	$\displaystyle \frac{5{,}53}{5{,}57}$	$\displaystyle \cos^{-1}\left(\right)$
$\displaystyle \alpha$	$=$	$\displaystyle \cos^{-1}\left(\frac{5{,}53}{5{,}57}\right)$
	$=$	$\displaystyle 6{,}870...$
	$≈$	$\displaystyle 6{,}87°$

$\displaystyle \tan\beta$	$=$	$\displaystyle \frac{9}{100}$	$\displaystyle \tan^{-1}\left(\right)$
$\displaystyle \beta$	$=$	$\displaystyle \tan^{-1}\left(\frac{9}{100}\right)$
	$=$	$\displaystyle 5{,}142...$
	$≈$	$\displaystyle 5{,}14°$

$\displaystyle \sin\alpha$	$=$	$\displaystyle \frac{217}{1435}$	$\displaystyle \sin^{-1}\left(\right)$
$\displaystyle \alpha$	$=$	$\displaystyle \sin^{-1}\left(\frac{217}{1435}\right)$
	$=$	$\displaystyle 8{,}697...$
	$≈$	$\displaystyle 8{,}70°$

$\displaystyle y$	$=$	$\displaystyle -x^2+4x-1$
	↓	$x=0{,}5$
	$=$	$\displaystyle -0{,}5^2+4\cdot0{,}5-1$
	$=$	$\displaystyle -0{,}25+2-1$
	$=$	$\displaystyle 0{,}75$

$\displaystyle 0$	$=$	$\displaystyle x^2-4x+1$
	↓	$p=-4\qquad q=1$
$\displaystyle x_{1{,}2}$	$=$	$\displaystyle -\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}$
	$=$	$\displaystyle -\frac{\left(-4\right)}{2}\pm\sqrt{\left(\frac{-4}{2}\right)^2-1}$
	$=$	$\displaystyle 2\pm\sqrt{3}$
$\displaystyle \Rightarrow\ x_1$	$=$	$\displaystyle 2+\sqrt{3}=3{,}73\$
$\displaystyle \Rightarrow\ x_2$	$=$	$\displaystyle 2-\sqrt{3}=0{,}27$