Wahlteil 1
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Aufgaben zu Prüfung IGS E 2023, Wahlteil 1. Zum Download hier.
- 1
Aufgabe 5
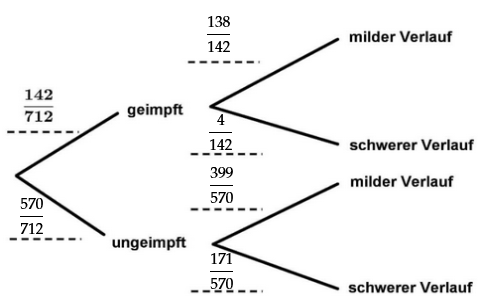
FSME ist eine Viruserkrankung, die durch Zecken übertragen wird. Eine Impfung kann vor einem schweren Verlauf der Erkrankung schützen.
Im Jahr 2020 wurde bei 712 Personen eine FSME-Infektion festgestellt. Davon waren 142 geimpft.
Von den geimpften Personen hatten 4 einen schweren Verlauf.
der Ungeimpften hatten einen milden Verlauf.

Bestätige durch eine Rechnung, dass von den Infizierten ca. geimpft waren. (1 BE)
Vervollständige die Vierfeldertafel. (3 BE)
Von den 712 Infizierten wird eine Person zufällig ausgewählt.
Im Baumdiagramm in Teilaufgabe (d) ist bereits der Wert eingetragen.
Gib die Bedeutung des Werts im Sachzusammenhang an. (2 BE)
Trage die fehlenden Wahrscheinlichkeiten in das Baumdiagramm ein. (3 BE)
Berechne die Wahrscheinlichkeit, dass die zufällig ausgewählte Person geimpft ist und einen milden Verlauf hat. Gib deine Lösung auch in Prozent an. (2 BE)
Berechne die Wahrscheinlichkeit, dass die zufällig ausgewählte Person einen milden Verlauf hat. Gib deine Lösung auch in Prozent an. (2 BE)
Eine Person mit schwerem Verlauf wird zufällig ausgewählt.
Berechne die Wahrscheinlichkeit, dass die Person geimpft ist. Gib deine Lösung auch in Prozent an. (2 BE)
Hanke möchte zum Campen ins Emsland fahren. Das Emsland ist ein FSME-Risikogebiet.
Bei der Zeckenbisse wird die Person infiziert. Hanke überlegt, ob er sich impfen lässt.
Berechne die Wahrscheinlichkeit, dass Hanke nicht infiziert wird, falls er von zwei Zecken gebissen wird. (2 BE)
Für den Fall, dass Hanke von vier Zecken gebissen wird, rechnet er:
Hanke sagt: „Wenn ich als Ungeimpfter von vier Zecken gebissen werde, beträgt die Wahrscheinlichkeit, schwer zu erkranken, ."
Erkläre, wie Hanke mithilfe seiner Rechnungen zu der Aussage kommt. (3 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?