Wahlteil 2
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Aufgaben zu Prüfung IGS E 2021, Wahlteil 2. Zum Download hier.
- 1
Aufgabe 5
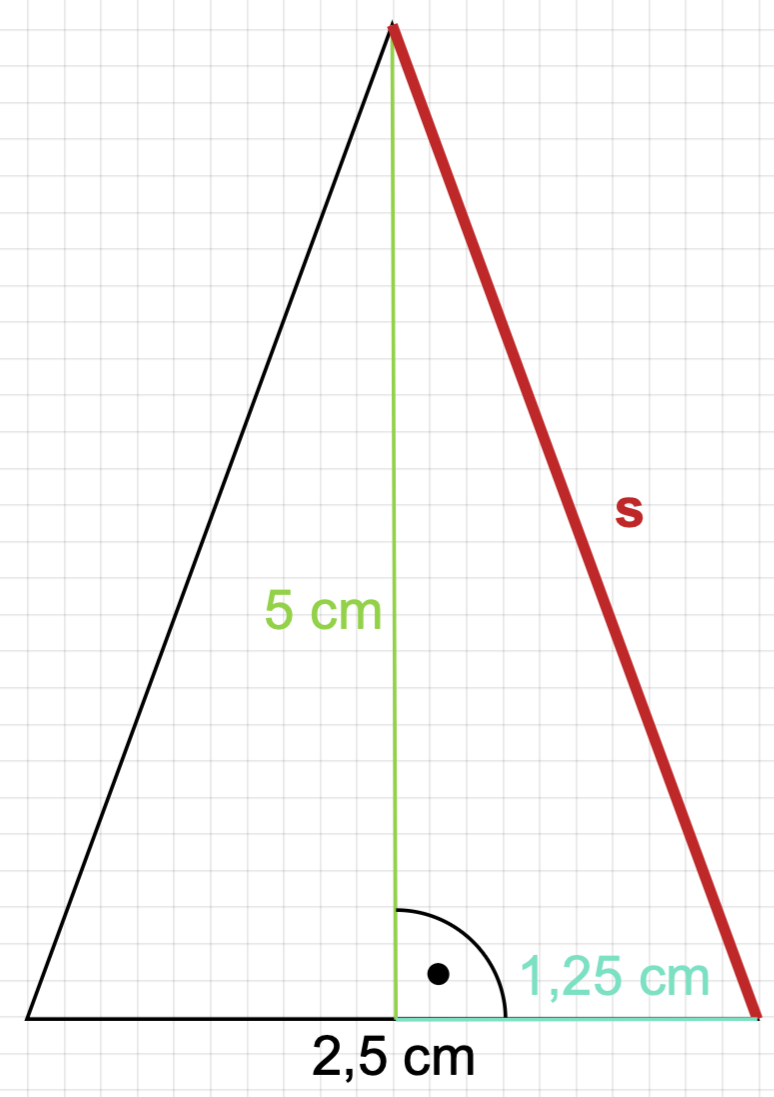
Eine Süßwarenfabrik stellt Pralinen aus Marzipan her.
Die Pralinen haben die Form eines Kegels.
Die Grundfläche hat einen Durchmesser von
Die Höhe des Kegels beträgt .

Abbildung nicht maßstabsgerecht
Berechne das Volumen einer Praline. (2 BE)
Berechne die Seitenhöhe des Kegels.
Erstelle eine Skizze zu deiner Rechnung. (3 BE)
Die gesamte Oberfläche der Praline wird mit Kakaopulver bedeckt.
Bestimme diese bedeckte Fläche. (2 BE)
(Wenn du b) nicht gelöst hast, verwende .)
Die Verpackung der Pralinen hat die Form eines Quaders mit einer Länge von , einer Breite von und einer Höhe von .
In einer Verpackung sind 10 Pralinen.
Zeige, dass weniger als des Volumens der Verpackung mit Pralinen gefüllt ist. (3 BE)
(Wenn du a) nicht gelöst hast, verwende .)
Die Süßwarenfirma möchte neue Pralinen auf den Markt bringen, die das gleiche Volumen wie die kegelförmigen Pralinen haben. Die neuen Pralinen sollen die Form einer Kugel haben.
Zeige durch eine Rechnung, dass der Radius der kugelförmigen Praline ist. (2 BE)

Abbildung nicht maßstabsgerecht
Die kugelförmige Praline soll einen dicken Schokoladenüberzug erhalten.
Bestimme den neuen Durchmesser der Praline mit Schokoladenüberzug. (1 BE)
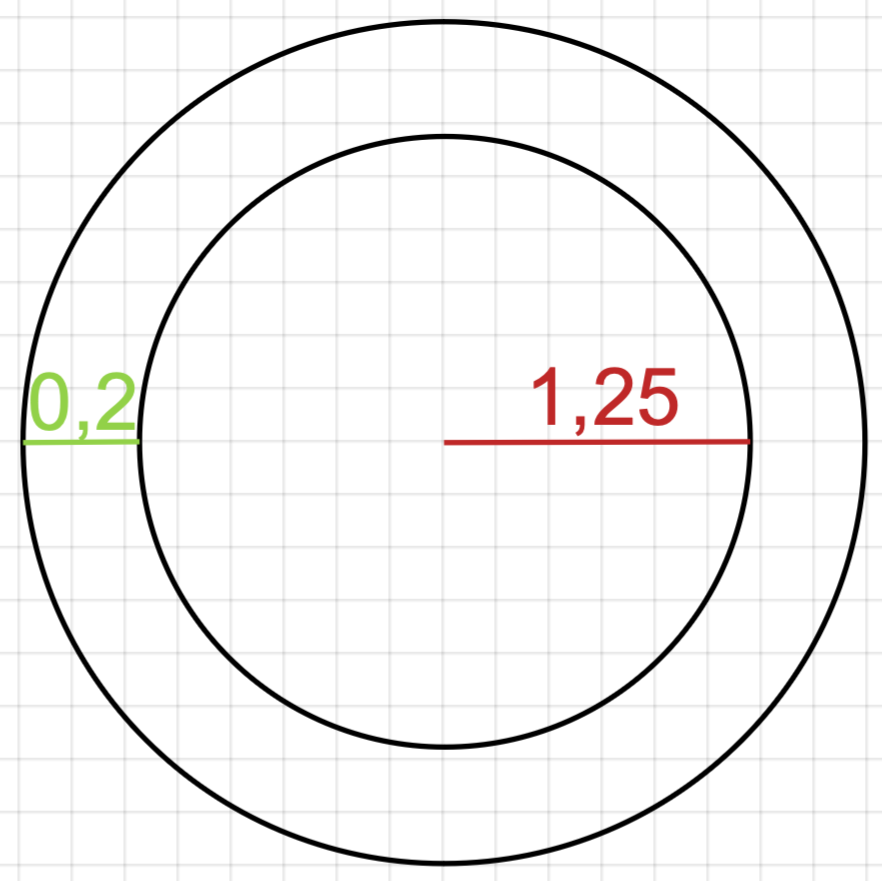
Hier ist ein Querschnitt durch die Mitte der Praline ohne Schokoladenüberzug abgebildet.
Berechne den Maßstab des Querschnitts.
Zeichne in diesem Querschnitt den Schokoladenüberzug maßstabsgerecht ein. (3 BE)
Berechne das Volumen des Schokoladenüberzugs einer Praline. (3 BE)
Der Kegel und die Kugel haben ohne den Schokoladenüberzug das gleiche Volumen.
Martin wundert sich, dass in diesem Fall auch die Radien von Kugel und Kegel gleich sind. Er vergleicht beide Volumenformeln und sagt: „Die Radien müssen gleich sein, weil ist.“
Nimm Stellung zu Martins Aussage. (1 BE)
Vergleiche dazu die Volumenformeln des Kegels und der Kugel.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?