Springe zum Inhalt oder Footer
SerloDie freie Lernplattform
Dieser Inhalt wurde gelöscht.

Aufgabe 1C

Gegeben ist die auf R\mathbb{R} definierte Funktion ff mit f(x)=−1100⋅(1500x4−18x3+52x2−45x)f(x)=-\frac{1}{100} \cdot\left(\frac{1}{500} x^{4}-\frac{1}{8} x^{3}+\frac{5}{2} x^{2}-45 x\right). Der Querschnitt eines Deichs wird durch die von dem Graphen der Funktion ff und der xx-Achse eingeschlossenen Fläche modelliert. Dabei werden xx und f(x)f(x) in Metern (m)(m) angegeben.

  1. Die Abbildung zeigt den Graphen von ff. Markieren Sie in der Abbildung auf der xx-Achse das Intervall, in dem der Deich mindestens 5m5 m hoch ist.

    Ein moderner Deich ist etwa fünfmal so breit wie er hoch ist.

    Entscheiden Sie, ob dieser Deich diese Regel erfüllt, und begründen Sie Ihre Entscheidung nur mithilfe der Abbildung. (5BE)

    Bild

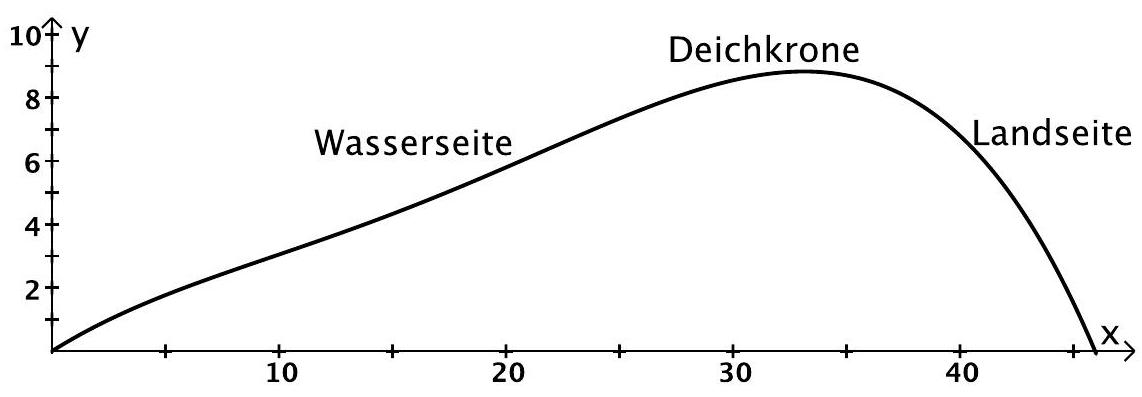
  2. Berechnen Sie die durchschnittliche Steigung des Deichs im Intervall [0;30][0 ; 30].

    Bestimmen Sie die größte Steigung des Deichs im Intervall [0;30].[0;30].

    Berechnen Sie den Neigungswinkel des Deichs an der Stelle x=0x=0. (9BE)

  3. In den Deich eindringendes Wasser teilt den Querschnitt des Deiches in einen unteren feuchten und einen oberen trockenen Bereich. Die Trennlinie zwischen dem trockenen und feuchten Bereich nennt man Sickerlinie. Bei einem bestimmten Wasserstand wird die Sickerlinie innerhalb des Deichs durch die auf R\mathbb{R} definierte Funktion gg mit g(x)=20⋅e−0,1xg(x)=20 \cdot e^{-0{,}1 x} beschrieben. xx und g(x)g(x) werden in Metern (m)(m) angegeben.

    Berechnen Sie die Höhe, in der die Sickerlinie auf der Wasserseite des Deichs beginnt.

    Begründen Sie ohne Rechnung, dass die Sickerlinie stets oberhalb des Bodens verläuft.

    Berechnen Sie den prozentualen Anteil des feuchten Bereichs im Querschnitt des

    Deichs. (10BE)

  4. Die Sickerlinie verändert sich mit dem Wasserstand. Sie wird beschrieben durch die auf R\mathbb{R} definierte Funktion hh mit h(x)=a⋅e−0,1x,xh(x)=a \cdot e^{-0{,}1 x}, x und h(x)h(x) in Metern (m)(m).

    Bestimmen Sie einen Näherungswert für aa, sodass hh den Beginn der Sickerlinie in der Höhe von 2m2 m auf der Wasserseite beschreibt. (4BE)

  5. Der Bereich der Deichkrone soll abgeplattet werden. Dazu wird Material abgetragen. Der Querschnitt des Deichs wird dabei so verändert, dass der obere Rand im Bereich der Deichkrone parallel zur Horizontalen verläuft.

    Berechnen Sie die Breite des abgeplatteten Bereichs, wenn der Deich genau 8 m8 \mathrm{~m} hoch sein soll.

    Berechnen Sie die Höhe des Deichs, wenn der abgeplattete Bereich 9m9 m breit ist. (7BE)