Bestimmen Sie die Wahrscheinlichkeit dafür, dass von $100$ zufällig ausgewählten Paketen

• genau neun das Ziel B haben.

• weniger als neun das Ziel B haben.

(4BE)

Unter $100$ zufällig ausgewählten Paketen haben genau neun das Ziel B.

Berechnen Sie die prozentuale Abweichung dieser Anzahl vom Erwartungswert für die

Anzahl von Paketen mit dem Ziel B unter 100 zufällig ausgewählten Paketen. (3BE)

Im Paketzentrum werden $20$ Pakete zufällig ausgewählt.

Eines der anderen Ziele ist Ziel C. Die Wahrscheinlichkeit dafür, dass von den $20$ ausgewählten Paketen keines das Ziel C hat, beträgt etwa $54 \%$.

Ermitteln Sie den Anteil der Pakete mit dem Ziel $\mathrm{C}$ unter allen Paketen, die pro Jahr im Paketzentrum angeliefert werden. (4BE)

Die Wahrscheinlichkeit eines Ereignisses im Sachzusammenhang kann mit dem Term

$\def\arraystretch{1.25} 0{,}9^{14} \cdot\left[0{,}9^{6}+\left(\begin{array}{l}6 \\ 1\end{array}\right) \cdot 0{,}1 \cdot 0{,}9^{5}+\left(\begin{array}{l}6 \\ 2\end{array}\right) \cdot 0{,}1^{2} \cdot 0{,}9^{4}+\left(\begin{array}{l}6 \\ 3\end{array}\right) \cdot 0{,}1^{3} \cdot 0{,}9^{3}\right]$

berechnet werden.

Geben Sie ein passendes Ereignis an. (2BE)

Alle im Paketzentrum angelieferten Pakete werden im Rahmen der Sortierung gewogen.

$5 \%$ der Pakete haben ein Gewicht von mehr als $10 \mathrm{~kg}$ und gelten damit als schwer. Von den Paketen mit dem Ziel A sind $8 \%$ schwer.

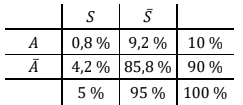
Untersuchen Sie, ob der Anteil der Pakete mit Ziel A unter den schweren Paketen ebenso groß ist wie unter den nicht-schweren Paketen. (4BE)

Von den Paketen, die das Ziel B haben, sind $2 \%$ schwer.

Berechnen Sie den Anteil der schweren Pakete unter denen, die weder Ziel A noch Ziel B haben. (3BE)