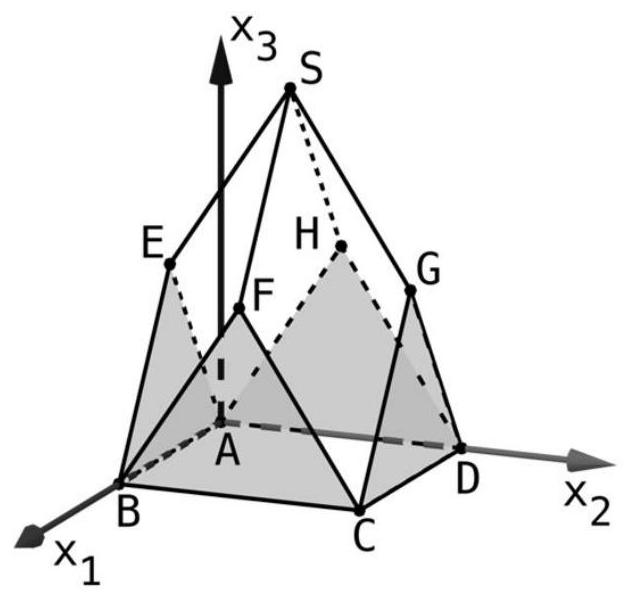
Die Ebene $L$ enthält die Punkte $C, G$ und $F$.

Geben Sie eine Gleichung von $L$ in Parameterform an und zeigen Sie, dass auch $S$ in $L$ liegt. (4BE)

Weisen Sie nach, dass das Viereck CGSF eine Raute ist. (3BE)

Berechnen Sie die Größe des Innenwinkels des Vierecks $CGSF$ im Punkt $S$ sowie den gesamten Flächeninhalt der Dachflächen. (5BE)

Die Gerade $q_{1}$ verläuft durch $S$ und $F$, die Gerade $q_{2}$ durch $S$ und $G$. Die beiden Geraden schneiden die $x_{1} x_{2}$-Ebene in den Punkten $Q_{1}$ bzw. $Q_{2}$.

Geben Sie das Verhältnis des Abstands von $Q_{1}$ und $Q_{2}$ zum Abstand von $F$ und $G$ an.

Begründen Sie Ihre Angabe, ohne die Koordinaten von $Q_{1}$ und $Q_{2}$ zu berechnen. (3BE)

Zur Stabilisierung wird zwischen den durch $E$ und $G$ dargestellten Giebelspitzen ein gerader Stahlträger montiert. Vom Mittelpunkt dieses Stahlträgers aus soll eine möglichst kurze Stütze zum durch $\overline{S F}$ dargestellten Balken verlaufen. Der Punkt, in dem die Stütze auf den Balken trifft, wird im Modell mit $R$ bezeichnet.

Berechnen Sie die Koordinaten von $R$. (5BE)