Teil 1 Analysis

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgaben zum Ausdrucken als PDF findest du hier.

Die Aufgaben in diesem Ordner sollen ohne Hilfsmittel wie Taschenrechner oder Formelsammlung bearbeitet werden.

1
Gegeben ist die Funktion $g : x \to \frac{(x + 2) (x - 2)}{- x (x - 2)}$ mit ihrer maximalen Definitionsmenge $D_{g} \subseteq ℝ$ . Ihr Graph wird mit $G_{g}$ bezeichnet. Geben Sie $D_{g}$ sowie die Art der Definitionslücken von $g$ an und untersuchen Sie $g$ auf Nullstellen. Geben Sie auch jeweils die Art und die Gleichung aller Asymptoten von $G_{g}$ an.
2
In der untenstehenden Abbildung ist ein Ausschnitt des Graphen $G_{f}$ einer gebrochenrationalen Funktion $f$ mit der Definitionsmenge $D_{f} = ℝ$ dargestellt. $G_{f}$ besitzt den absoluten Hochpunkt $H (0,8 | f (0,8))$ , ist im Intervall $[0,8; + \infty [$ streng monoton fallend und besitzt die x-Achse als waagrechte Asymptote. Für die Funktion $h$ gilt: $h (x) = \ln (f (x))$ . Die maximale Definitionsmenge der Funktion $h$ ist $D_{h} =] - 2; + \infty [$ .
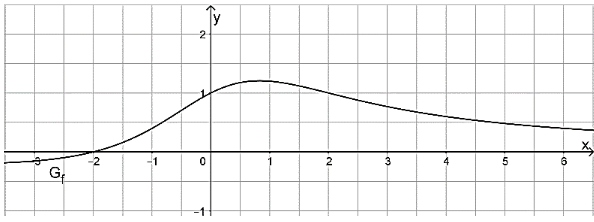
1. Geben Sie das Verhalten der Funktionswerte von $h$ an den Rändern von $D_{h}$ an. [3 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwert bestimmen
  Gib das Verhalten der Funktionswerte von $h$ an den Rändern von $D_{h}$ an
  Gegeben: $D_{h} =] - 2; + \infty [$
  Linker Rand: $x = - 2^{+}$ und $f (- 2) = 0$
  $\lim_{x \to - 2^{+}} \ln (\underset{0}{\underset{⏟}{f (x)}}) = - \infty$
  Rechter Rand:
  $\lim_{x \to + \infty} \ln (\underset{\to 0}{\underset{⏟}{f (x)}}) = - \infty$ (Die $x$ -Achse ist waagrechte Asymptote.)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Gegeben: $D_{h} =] - 2; + \infty [$
  Linker Rand: $x = - 2^{+}$ und $f (- 2) = 0$
  Berechne $\lim_{x \to - 2^{+}} \ln (f (x))$ .
  Rechter Rand: Berechne $\lim_{x \to + \infty} \ln (f (x))$ . Beachte, die $x$ -Achse ist waagrechte Asymptote.
2. Geben Sie mithilfe der Abbildung die Nullstellen der Funktion $h$ an. Die abzulesenden Werte sind ganzzahlig. [2 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
  Gib mithilfe der Abbildung die Nullstellen der Funktion $h$ an
  $h (x) = 0 \Leftrightarrow f (x) = 1$
  Aus der Abbildung folgt: $f (0) = 1$ und $f (2) = 1$
  Die Nullstellen der Funktion $h$ sind $x = 0$ und $x = 2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  $h (x) = 0 \Leftrightarrow f (x) = 1$
  Wo gilt $f (x) = 1 ?$
3. Begründen Sie, dass der Graph der Funktion $h$ genau einen Extrempunkt hat und geben Sie die Art sowie die x-Koordinate dieses Extrempunktes an. [3 BE]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
  Begründe, dass der Graph der Funktion $h$ genau einen Extrempunkt hat und gib die Art sowie die x-Koordinate dieses Extrempunktes an
  $h (x) = \ln (f (x)) \Rightarrow h^{'} (x) = \frac{1}{f (x)} \cdot f^{'} (x) = \frac{f^{'} (x)}{f (x)}$ (Beachte beim Ableiten die Kettenregel.)
  Dabei ist $f (x) > 0$ in $D_{h}$ $\Rightarrow$ der Vorzeichenwechsel von $h^{'} (x)$ entspricht dem Vorzeichenwechsel von $f^{'} (x)$ .
  ⁣ $G_{f}$ besitzt den absoluten Hochpunkt $H (0,8 | f (0,8))$ und ist im Intervall $[0,8; + \infty [$ streng monoton fallend, mit der $x$ -Achse als waagrechte Asymptote.
  Damit besitzt auch $G_{h}$ bei $x = 0,8$ einen Hochpunkt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $h^{'} (x)$ . Beachte beim Ableiten die Kettenregel.
  Es ist $f (x) > 0$ in $D_{h}$ $\Rightarrow$ der Vorzeichenwechsel von $h^{'} (x)$ entspricht dem Vorzeichenwechsel von $f^{'} (x)$ .
3
Gegeben ist die Funktion $k : x \to \frac{x + 1}{e^{x} - 1}$ mit ihrer maximalen Definitionsmenge $D_{k} = ℝ$ $∖ {0}$ . Entscheiden Sie begründet, welche der folgenden Aussagen jeweils wahr oder falsch sind. [4 BE]
1. Der Graph der Funktion $k$ hat eine senkrechte Asymptote.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Asymptote
  Der Graph der Funktion $k$ hat eine senkrechte Asymptote
  Die Aussage ist wahr.
  $x = 0$ ist eine senkrechte Asymptote von $G_{k}$ .
  $G_{k}$ hat eine Polstelle bei $x = 0$ , denn $N (x) = e^{x} - 1$ ist null für $x = 0 \Rightarrow N (0) = e^{0} - 1 = 1 - 1 = 0$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  $G_{k}$ hat eine Polstelle bei $x = 0$ . Was bedeutet das?
2. $x \to \infty \Rightarrow k (x) \to - 1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwert bestimmen
  $x \to \infty \Rightarrow k (x) \to - 1$ ?
  Berechne $\lim_{x \to \infty} \frac{\overset{\to \infty}{\overset{⏞}{x + 1}}}{\underset{\to \infty}{\underset{⏟}{\underset{\to \infty}{\underset{⏟}{e^{x}}} - 1}}} = 0 \neq - 1$
  Die e-Funktion ( $e^{x}$ ) wächst für $x$ gegen unendlich schneller als jede Potenzfunktion ( $x^{n}$ ), deshalb erhält man den Grenzwert null.
  Die Aussage ist also falsch.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $\lim_{x \to \infty} \frac{x + 1}{e^{x} - 1}$ .
4
Berechnen Sie den Wert des bestimmten Integrals $\int_{1}^{2} (\frac{1}{x^{2}} - 2 x + 5) d x$ . [4 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrale
Berechne den Wert des bestimmten Integrals
$\int_{1}^{2} (\frac{1}{x^{2}} - 2 x + 5) d x = {[- \frac{1}{x} - x^{2} + 5 x]}_{1}^{2} = (- \frac{1}{2} - 4 + 10) - (- 1 - 1 + 5) = 5,5 - 3 = 2,5$
Der Wert des bestimmten Integrals beträgt $2,5 FE$ .
Berechne das bestimmte Integral.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Teil 1 Analysis

Gib das Verhalten der Funktionswerte von h an den Rändern von Dh an

Hast du eine Frage oder Feedback?

Gib mithilfe der Abbildung die Nullstellen der Funktion h an

Hast du eine Frage oder Feedback?

Begründe, dass der Graph der Funktion h genau einen Extrempunkt hat und gib die Art sowie die x-Koordinate dieses Extrempunktes an

Hast du eine Frage oder Feedback?

Der Graph der Funktion k hat eine senkrechte Asymptote

Hast du eine Frage oder Feedback?

x→∞⇒k(x)→−1 ?

Hast du eine Frage oder Feedback?

Berechne den Wert des bestimmten Integrals

Gib das Verhalten der Funktionswerte von $h$ an den Rändern von $D_{h}$ an

Gib mithilfe der Abbildung die Nullstellen der Funktion $h$ an

Begründe, dass der Graph der Funktion $h$ genau einen Extrempunkt hat und gib die Art sowie die x-Koordinate dieses Extrempunktes an

Der Graph der Funktion $k$ hat eine senkrechte Asymptote

$x \to \infty \Rightarrow k (x) \to - 1$ ?