Aufgabe 3B
Betrachtet wird der Stumpf der schiefen Pyramide . Die Grundfläche mit und sowie die Deckfläche des Stumpfs mit , und sind quadratisch.
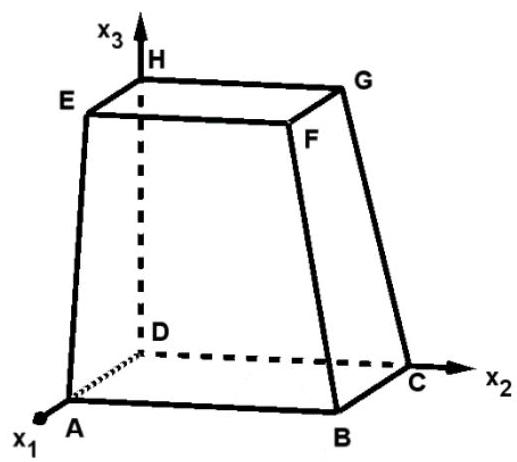
Berechnen Sie
die Länge der Strecke
die Koordinaten des Mittelpunktes der Strecke .
(3BE)
Erläutern Sie den folgenden Ansatz zur Berechnung der Koordinaten der Pyramidenspitze :
(3BE)
Bestimmen Sie das Volumen des Stumpfs. (3BE)
Der Pyramidenstumpf wird soweit um die Kante gedreht bis die Fläche in der-Ebene liegt.
Geben Sie die Koordinaten eines Bildpunktes an. (2BE)
Der Mittelpunkt der Kante und der Mittelpunkt der Kante liegen auf der Gerade mit .
Die Punkte der Kante lassen sich in der Form darstellen.
Für einen Punkt der Kante schneidet die Gerade durch und die Gerade .
Berechnen Sie den zugehörigen Wert von . (4BE)
Es gibt Punkte der Kante , für die der von den Strecken und eingeschlossene Winkel größer als ist.
Ermitteln Sie die zugehörigen Werte von . (5BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
