Prüfungsteil 2 2023
🎓 Prüfungsbereich für Nordrhein-Westfalen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Aufgaben aus dem Prüfungsteil 2 der ZP 10 Mathe 2023 für die gymnasiale Differenzierung mit ausführlichen Musterlösungen.
Für diese Aufgaben stehen dir in der Zentralen Prüfung 90 Minuten Bearbeitungszeit zur Verfügung. Taschenrechner und Formelsammlung sind für diesen Prüfungsteil erlaubt.
- 1
Aufgabe 1: Herzlich willkommen
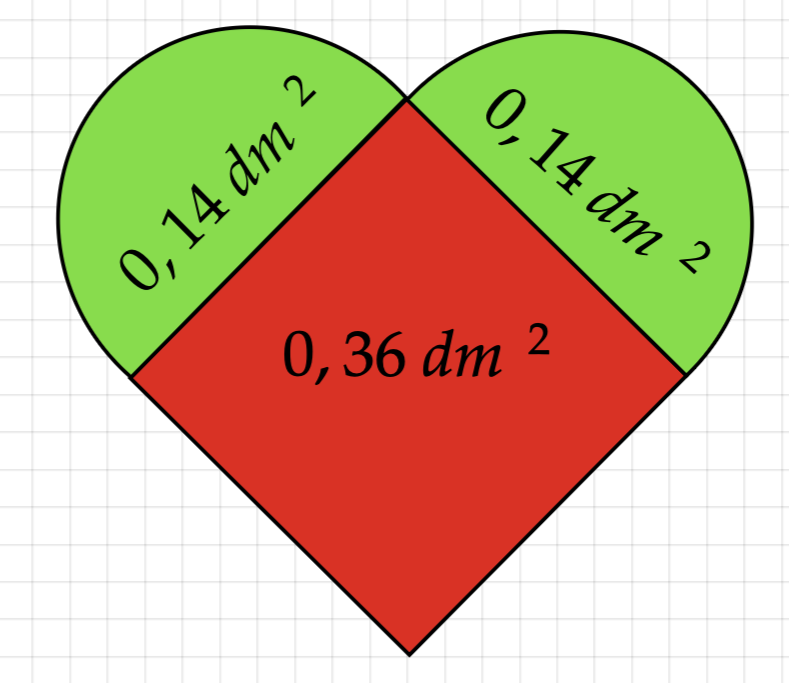
Eine Firma produziert herzförmige Dekoanhänger aus Metall. Jedes Herz besteht aus einem Quadrat mit der Kantenlänge , an das zwei Halbkreise mit einem Radius von jeweils angesetzt sind (Abbildung).
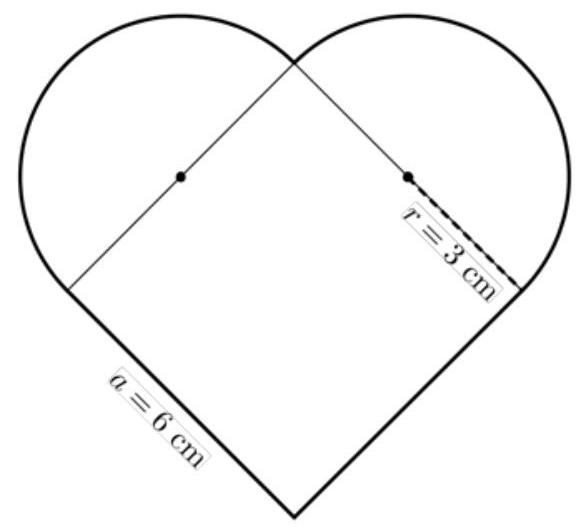
Abbildung: geometrische Form eines Herzens
Zeichne ein Herz in Originalgröße in dein Heft. (3 P)
Die Herzen werden aus dünnen Metallblechen hergestellt. des Metallblechs wiegt .
Berechne das Gewicht eines Herzens. (3 P)
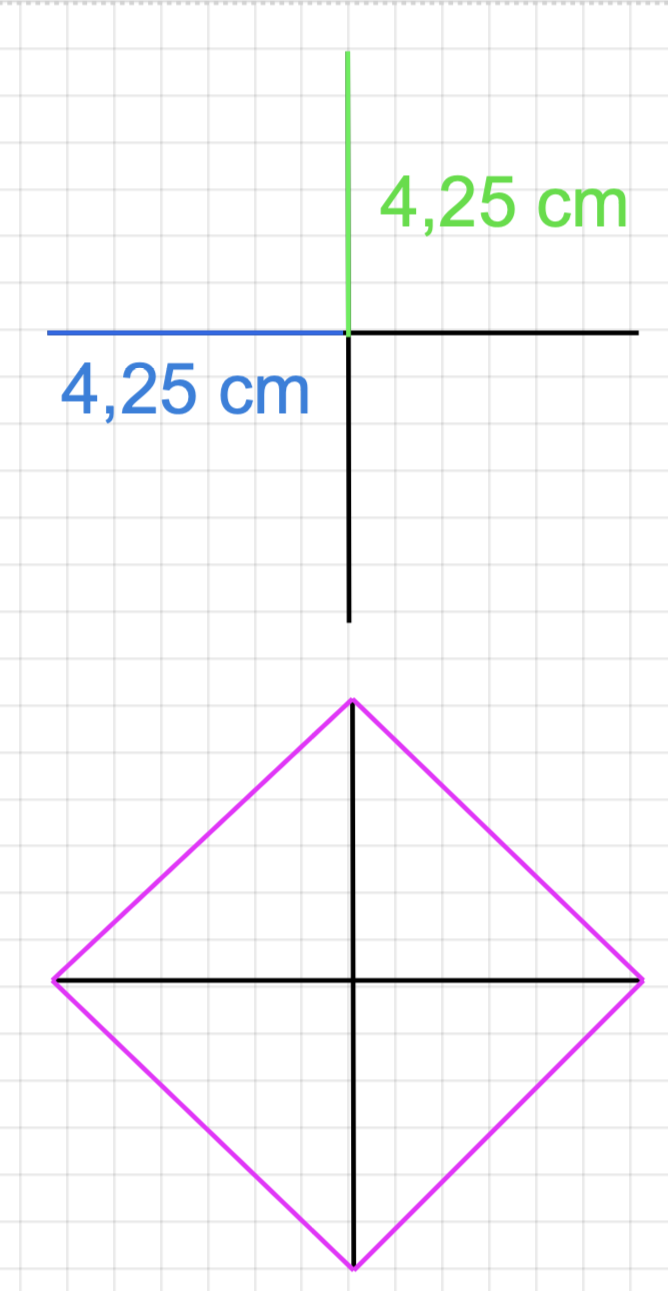
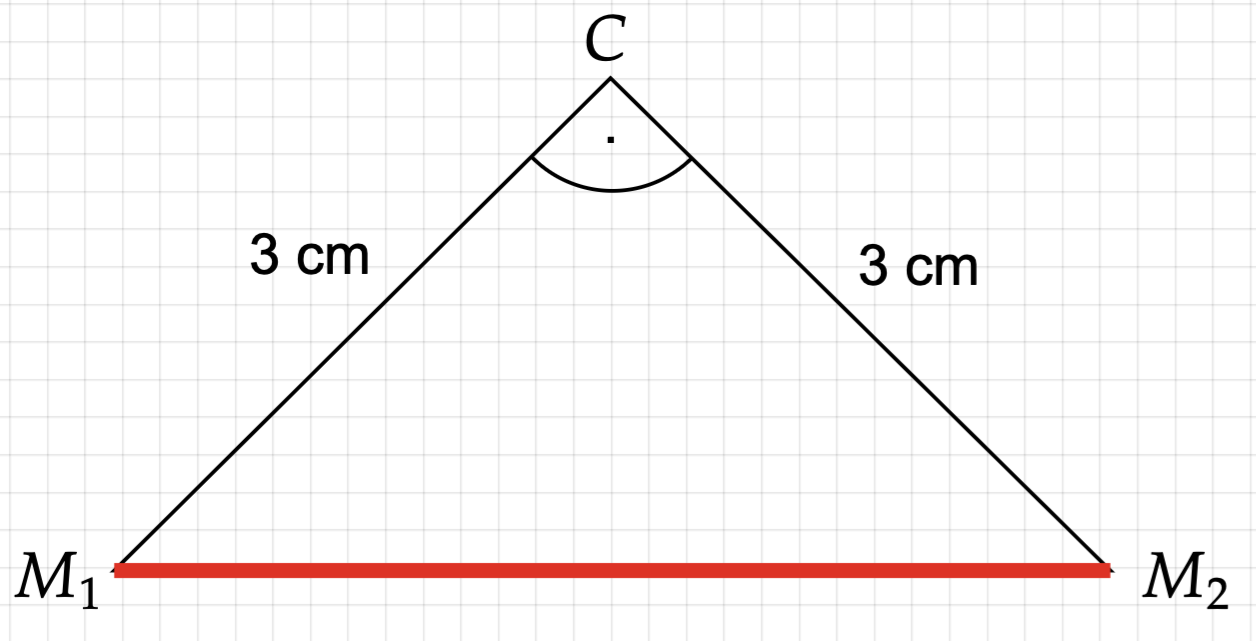
Um die Breite und die Höhe eines Herzens zu bestimmen, wird eine Skizze angefertigt. Hier gilt: Die Strecke entspricht der Breite geht durch die Mittelpunkte und der angesetzten Halbkreise.
Berechne die Breite eines Herzens. (3 P)
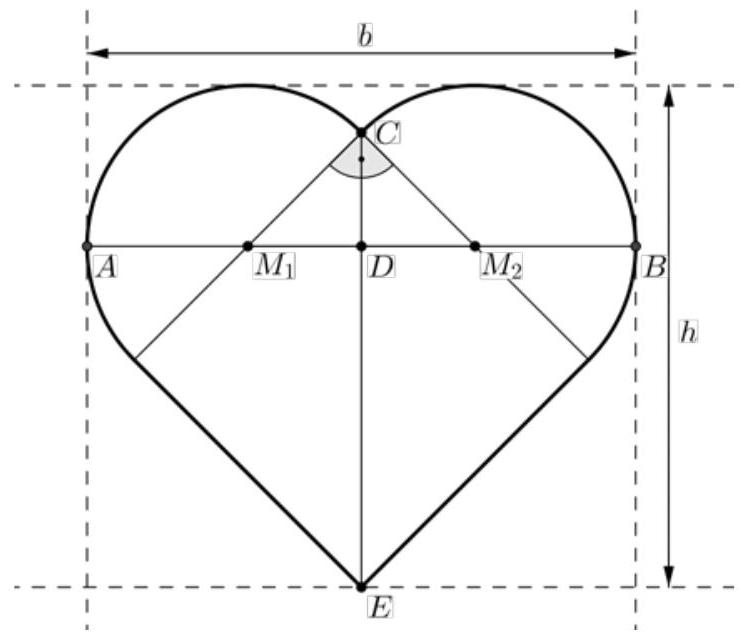
Skizze zur Berechnung der Breite und der Höhe
Mithilfe der Abbildung in (c) kann die Höhe der Herzen berechnet werden.
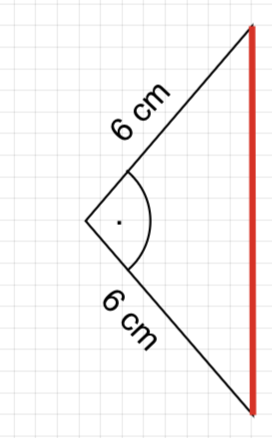
(1) Berechne die Länge der Strecke . (3 P)
(2) Begründe, dass für die Höhe der Herzen gilt: . (1 P)
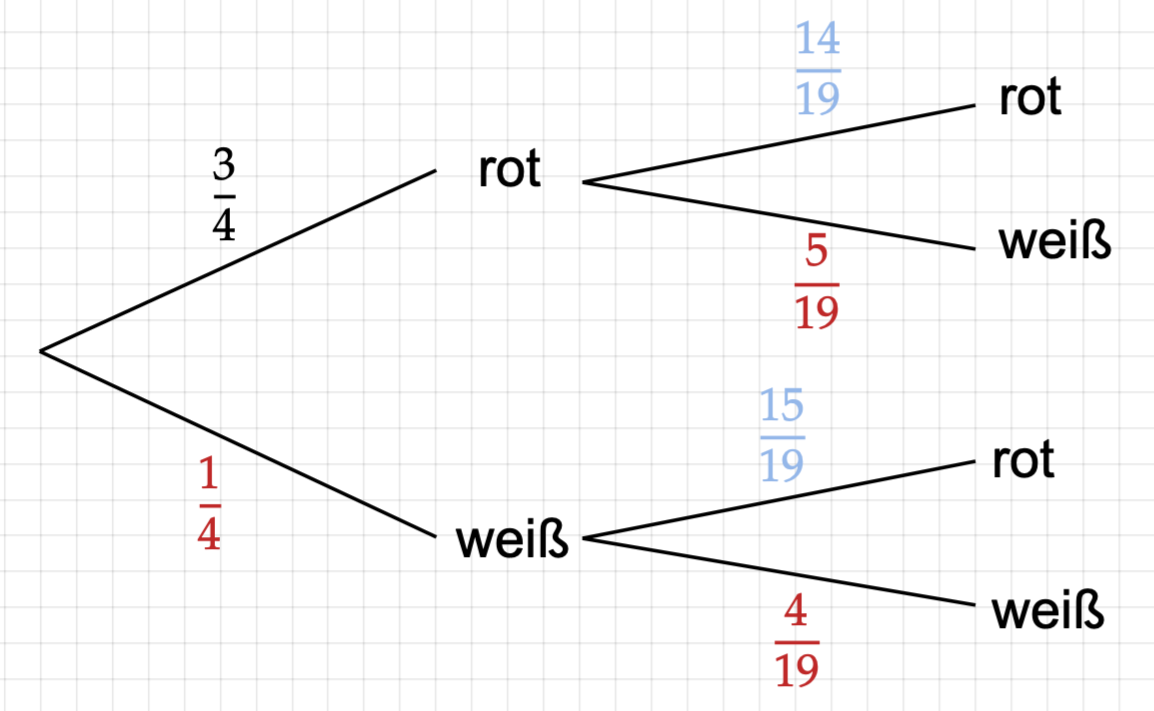
Die Herzen werden in den Farben rot und weiß produziert und farblich gemischt in Kartons verpackt. Beim Fabrikverkauf werden die Herzen angeboten. Die Kunden dürfen ohne hinzusehen nacheinander zwei Herzen aus dem Karton ziehen. Zu diesem Zufallsversuch gehört das folgende Baumdiagramm.
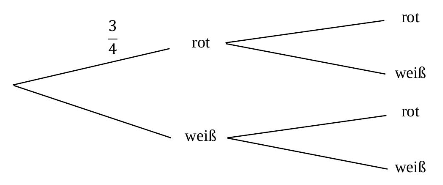
In einem Karton sind 15 Herzen rot, die restlichen Herzen sind weiß.
Begründe, dass sich in dem Karton insgesamt 20 Herzen befinden. (2 P)
Gesucht ist die Wahrscheinlichkeit, dass zwei verschiedenfarbige Herzen gezogen werden.
(1) Ergänze im Baumdiagramm die dafür notwendigen Wahrscheinlichkeiten. (2 P)
(2) Berechne die gesuchte Wahrscheinlichkeit. (2 P)
- 2
Aufgabe 2: Varroa-Milbe
Die Varroa-Milbe ist ein Schädling, der in jedem Bienenvolk lebt. Die Schülerinnen und Schüler der Bienen-AG untersuchen die Milbe mit einem Mikroskop.

Abbildung 1: Varroa-Milbe (vergrößert) Quelle: https://www.mikroskopieforum.de/index.php?topic=16864.0 (verändert)
Berechne die Länge und Breite der Milbe durch Messen der Pfeillängen und Anwenden des Maßstabs (Abbildung 1). (3 P)
Im Frühjahr ermitteln sie die Anzahl der Milben im Bienenvolk.
Im Internet finden sie die Faustregel, dass sich die Anzahl der Milben alle vier Wochen etwa verdoppelt. Sie kalkulieren die voraussichtliche Anzahl der Milben für die kommenden vier und acht Wochen. Die Werte halten sie in einer Tabelle fest.

Ergänze die fehlenden Werte in der Tabelle. (2 P)
Um die Entwicklung der Milben pro Woche vorauszusagen, beschreiben sie die Anzahl der Milben mit der folgenden Exponentialfunktion :
Gib die Bedeutung der Werte 308 und 1,19 im Zusammenhang an. (2 P)
Bestätige mithilfe der Funktionsgleichung, dass nach 12 Wochen ca. 2500 Milben vorhanden sind. (3 P)
Bei einer Anzahl von ca. 10000 Milben würde das Bienenvolk so großen Schaden nehmen, dass es nicht überleben kann.
Bestimme, nach wie vielen Wochen die Anzahl von 10000 Milben überschritten wird. (3 P)
Damit das Bienenvolk überlebt, wird nach 12 Wochen Ameisensäure eingesetzt. Dadurch wird die Anzahl von ca. 2500 Milben einmalig um reduziert.
Weise nach, dass durch die Behandlung mit der Ameisensäure die Anzahl von 10000 Milben 21 Wochen nach Beobachtungsbeginn nicht überschritten wird. (3 P)
- 3
Aufgabe 3: Zahlenpaare
Merle hat Spaß an Zahlen und ist immer auf der Suche nach Tricks, um den Rechenaufwand einer Aufgabe zu verringern. Bei der Addition der Zahlen von 1 bis 10 bemerkt sie:
„Die beiden Zahlen 1 und 10 ergeben zusammen 11, ebenso wie die beiden Zahlen 2 und 9, die Zahlen 3 und 8 usw. Da ich so fünf Zahlenpaare jeweils mit dem Wert 11 bilden kann, muss ich nur rechnen und erhalte das Ergebnis 55.“ (Abbildung 1)
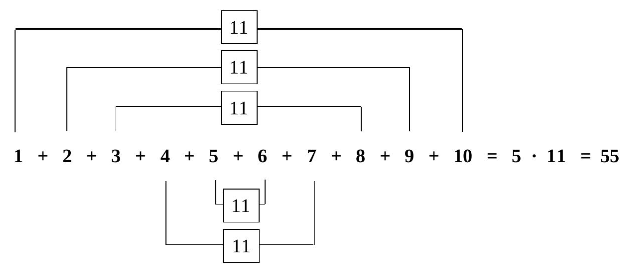
Abbildung 1: Rechentrick für die Addition der Zahlen von 1 bis 10
Merle verwendet den Trick für aufwendigere Additionen. Damit die Rechnungen übersichtlich bleiben, ersetzt sie fehlende Summanden durch Pünktchen. In Abbildung 2 ist Merles Berechnung für die Summe der Zahlen von 1 bis 30 dargestellt.
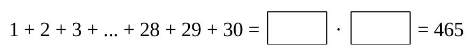
Abbildung 2: Addition der Zahlen von 1 bis 30
Begründe, dass in den Kästchen die Zahlen 15 bzw. 31 stehen müssen. (2 P)
Merle findet einen allgemeinen Term, um die Summe der Zahlen von 1 bis zu berechnen.
Sie notiert .
(1) Berechne mit dem Term den Wert der Summe für . (2 P)
(2) Erläutere die Bedeutung der Faktoren und im Zusammenhang mit dem Rechentrick. (2 P)
Merles Freund Silas nutzt ebenfalls den Term und notiert dafür .
Begründe, warum diese Rechnung nicht zu dem Rechentrick passen kann. (2 P)
Merle formt den Term um und erhält .
Berechne den Wert der Summe für mit diesem vereinfachten Term. (2 P)
(1) Berechne die beiden Lösungen der Gleichung . (4 P)
(2) Erkläre, warum nur eine Lösung für den Kontext sinnvoll ist. (2 P)
„Bei meinem Rechentrick muss man die Summanden paarweise zusammenfassen. Daher nehme ich an, dass meine Formel für ungerade Zahlen nicht gilt“, meint Merle.
Silas hat eine Idee: „Wenn eine ungerade Zahl ist, dann ist eine gerade Zahl. Für gerade Zahlen kann ich Merles Formel nutzen und anschließend die fehlende Zahl addieren.“
Zeige mit Silas Idee, dass für ungerade Zahlen der gilt. (3 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?