Heft 2 - B3

🎓 Prüfungsbereich für Schleswig-Holstein

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Hier findest du die Aufgaben und Lösungen des Mathe MSA 2021 Prüfungsteil 2 Aufgabe 3.

Link zur Formelsammlung

Ein Taschenrechner ist in diesem Prüfungsteil erlaubt.

1
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Fläche des gleichschenkligen Dreiecks $A B C$ ist begrenzt durch die $x$ -Achse und die Geraden $f$ und $g$ .
Die Eckpunkte des Rechtecks liegen auf der $x$ -Achse und den Geraden $f$ und $g$ .
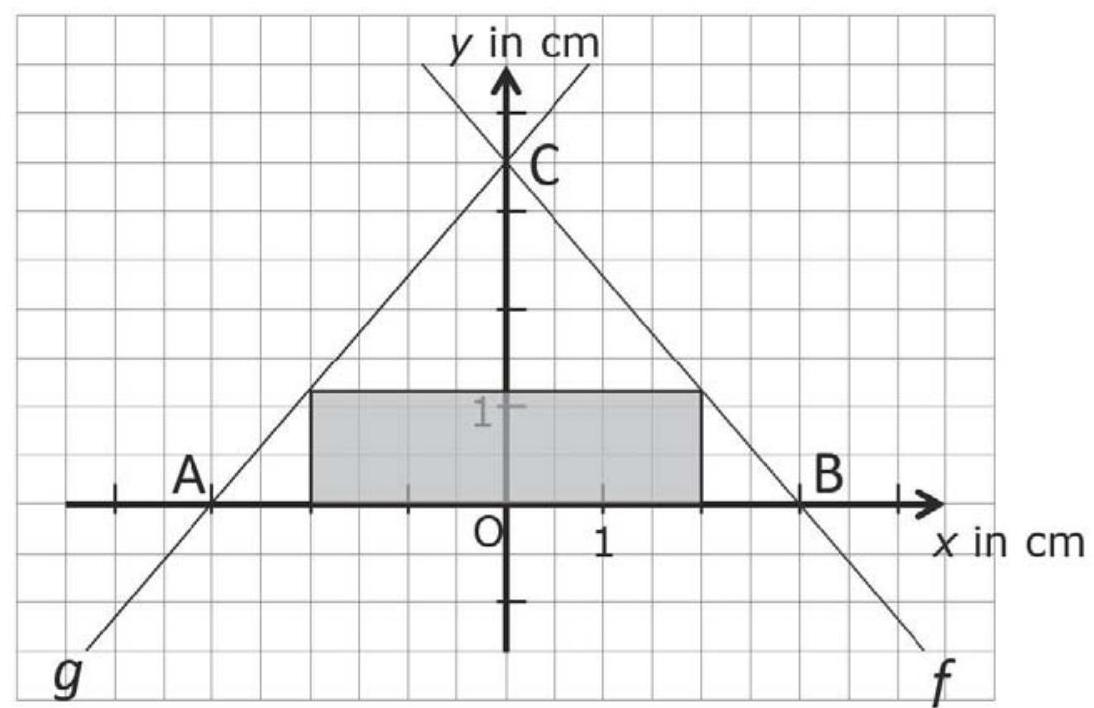
Die Gerade $g$ wird durch die Funktionsgleichung $g (x) = \frac{7}{6} x + 3,5$ beschrieben.
Gib die Funktionsgleichung für die Gerade $f$ an. (2 Punkte)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Bestimmen der Funktionsgleichung der Geraden $f :$
Allgemeine Form einer Geradengleichung:
$y = m x + b;$ $y - A c h s e n a b s c h n i t t b = 3,5$ (siehe Skizze)
$y = m x + 3,5$ einsetzen der Koordinaten des Punktes $A (3 | 0)$
$0 = 3 m + 3,5$
$- 3 m = 3,5$
$m = - \frac{3,5}{3}$ erweitern des Bruches mit $2 \Rightarrow m = - \frac{7}{6}$
Die Funktionsgleichung der Geraden $f$ lautet dann:
$f (x) = - \frac{7}{6} x + 3,5$
Schreibe die Funktionsgleichung in die Lücke.
Die allgemeine Form einer Geradengleichung lautet: $y = m x + b$ .
Der $y$ -Achsenabschnitt ist bekannt, setze die Koordinaten eines beliebigen Punktes der Geraden $f$ in die allgemeine Form ein und bestimme die Funktionsgleichung der Geraden $f$ .
2
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Tim untersucht den Flächeninhalt des Rechtecks. Er möchte wissen, wann es den größten Flächeninhalt hat.
1. Den Flächeninhalt des Rechtecks aus dem Beispiel bestimmt Tim auf die folgende Weise:
  Breite $b$ des Rechtecks: $4 c m$
  Höhe $h$ des Rechtecks: $g (- 2) = \frac{7}{6} \cdot (- 2) + 3,5 = 1,1 6 c m$
  Flächeninhalt des Rechtecks: $A = 4 \cdot 1,1 6 {c m}^{2} \approx 4,67 {c m}^{2}$
  Beschreibe, wie Tim vorgegangen ist. (3 Punkte)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt von Rechteck und Quadrat
  Bestimmen der Breite
  Aus der Zeichnung ist erkennbar, dass die Breite 4 Einheiten beträgt. Somit ist die Breite $b$ der Rechtecke: $4 c m$
  Bestimmen der Höhe
  Das Rechteck berührt den Funktionsgraphen von $g (x)$ aus Aufgabe 1 beim X-Wert $- 2$ . Durch Einsetzen in die Funktion erhält Tim:
  $g (- 2) = \frac{7}{6} \cdot (- 2) + 3,5 = 1,1 6$
  Die Höhe $h$ beträgt also: $1,1 6 c m$
  Berechnen des Flächeninhalts
  Der Flächeninhalt eines Rechtecks wird mit der Formel:
  $A = b \cdot h$
  Durch Einsetzen der Werte erhält Tim:
  $A = 4 \cdot 1,1 6 \approx 4,67$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme $b$ Mithilfe der Zeichnung
  Bestimme $h$ mithilfe der Funktionsgleichung
  Berechne den Flächeninhalt
2. Tim untersucht weitere solcher Rechtecke und notiert seine Ergebnisse in einer Tabelle.
  Breite $b$ in $cm$
  Flächeninhalt $A$ in ${cm}^{2}$
  1
  2,92
  2
  4,67
  3
  5,25
  4
  4,67
  5
  2,92
  Tim behauptet: „Mehr Möglichkeiten muss ich nicht untersuchen. Das Rechteck mit dem größten Flächeninhalt hat eine Breite von $3 c m$ .“
  Zeige, dass Tim recht hat. (2 Punkte)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertetabelle
  Der Zusammenhang zwischen der Breite der Rechtecke und dem Flächeninhalt ist quadratisch. Wir haben hier also die Wertetabelle einer Parabel vorliegen.
  In der Wertetabelle sind die Funktionswerte um $b = 3$ symmetrisch. Das heißt an dieser Stelle befindet sich der Scheitel der Parabel.
  Da der Scheitel der höchste bzw. tiefste Punkt einer Parabel ist, stimmt die Aussage von Tim.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Vergleiche die Wertetabelle mit einer Wertetabelle einer Parabel. Was fällt auf bezüglich der Symmetrie dieser Werte?
3. Stelle die Angaben aus der Tabelle in einem Koordinatensystem dar. (2 Punkte)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Das Koordinatensystem
  Einzeichnen der Werte
  Zeichne ein Koordinatensystem und trage die Werte in das Koordinatensystem ein. Achte dabei auf die richtige Beschriftung der Achsen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
In der Tabelle hat Tim seine Ergebnisse notiert.
Breite $b$ in $cm$
Flächeninhalt $A$ in ${cm}^{2}$
1
2,92
2
4,67
3
5,25
4
4,67
5
2,92
1. Die Angaben in Tims Tabelle lassen sich mithilfe der Gleichung einer quadratischen Funktion beschreiben.
  Tim behauptet: „Mit der Scheitelpunktform ergibt sich
  $k (x) = (x - 3)^{2} + 5,25$ .“
  Zeige, dass diese Scheitelpunktform nicht richtig ist. (1 Punkt)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
  Nachweis, dass diese Scheitelpunktform nicht richtig ist:
  Einsetzen von z. B. $4$ in $k (x)$
  $k (4) = (4 - 3)^{2} + 5,25$
  $k (4) = 6,25$
  $6,25 \neq 4,67 \Rightarrow$ Die Scheitelpunktform ist also nicht richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze einen Wert für $b$ aus der Tabelle in $k (x)$ ein und löse die Gleichung.
  Vergleiche das Ergebnis mit dem entsprechenden Wert des Flächeninhalts
  $A$ aus der Tabelle.
2. Bestimme die korrekte Funktionsgleichung von $k$ . (3 Punkte)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Öffnungsfaktor bestimmen
  Bestimmen der korrekten Funktionsgleichung $k (x)$ :
  $k (x) = a (x - 3)^{2} + 5,25$ Einsetzen eines Zahlenpaars aus der Tabelle
  $4,67 = a (4 - 3)^{2} + 5,25$
  $4,67 = a + 5,25 \Rightarrow a = - 0,58$
  Die korrekte Scheitelpunktform lautet dann:
  $k (x) = - 0,58 \cdot (x - 3)^{2} + 5,25$
  Hinweis:
  Der Funktionswert 4,67 ist ein gerundeter Wert. Der exakte Funktionswert ist $4 \frac{2}{3}$ , wenn Du mit diesem Wert rechnest, erhältst Du:
  $a = - \frac{7}{12}; \Rightarrow k (x) = - \frac{7}{12} \cdot (x - 3)^{2} + 5,25$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze ein Wertpaar aus der Tabelle in $k (x)$ ein und berechne den Öffnungsfaktor $a$ .
3. Erläutere für jede der beiden Nullstellen ihre Bedeutung für das Rechteck. (2 Punkte)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
  Bedeutung der Nullstellen:
  Das Rechteck hat die Breite $6 c m$ und somit eine Höhe
  von $0 c m$ , d.h. einen Flächeninhalt von $0 c m^{2}$ .
  Das Rechteck hat die Breite $0 c m$ und somit einen
  Flächeninhalt von $0 c m^{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Breite $b$ in $cm$	Flächeninhalt $A$ in ${cm}^{2}$
1	2,92
2	4,67
3	5,25
4	4,67
5	2,92

Breite $b$ in $cm$	Flächeninhalt $A$ in ${cm}^{2}$
1	2,92
2	4,67
3	5,25
4	4,67
5	2,92

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Heft 2 - B3

Bestimmen der Funktionsgleichung der Geraden f:

Bestimmen der Breite

Bestimmen der Höhe

Berechnen des Flächeninhalts

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Einzeichnen der Werte

Hast du eine Frage oder Feedback?

Nachweis, dass diese Scheitelpunktform nicht richtig ist:

Hast du eine Frage oder Feedback?

Bestimmen der korrekten Funktionsgleichung k(x):

Hast du eine Frage oder Feedback?

Bedeutung der Nullstellen:

Hast du eine Frage oder Feedback?

Bestimmen der Funktionsgleichung der Geraden $f :$

Bestimmen der korrekten Funktionsgleichung $k (x)$ :