Teil 1 lineare Algebra und analytische Geometrie

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Für die Vektoren $\vec{a_{k}}$ , $\vec{b}$ und $\vec{c}$ mit $k \in ℝ$ im $ℝ^{𝟛}$ gilt:
$\vec{a_{k}} = (\begin{array}{c} - 1 \\ 0 \\ 2 k \end{array})$ und $\vec{b} \times \vec{c} = (\begin{array}{c} 1 \\ 2 \\ - 2 \end{array})$
1. Bestimmen Sie die Maßzahl des Flächeninhalts des von den Vektoren $\vec{b}$ und $\vec{c}$ aufgespannten Dreiecks.
2. Ermitteln Sie, für welchen Wert für $k$ die Vektoren $\vec{a_{k}}$ , $\vec{b}$ und $\vec{c}$ linear abhängig sind.
2
In einem kartesischen Koordinatensystem des $ℝ^{𝟛}$ sind die Ebene $E : x_{1} + 3 x_{3} = 0$ und die Gerade $g : \vec{x} = (\begin{array}{c} - 1 \\ 0 \\ 1 \end{array}) + λ \cdot (\begin{array}{c} 2 \\ 1 \\ 0 \end{array})$ mit $λ \in ℝ$ gegeben.
1. Geben Sie jeweils die besondere Lage von $g$ und $E$ im Koordinatensystem an.
2. Ermitteln Sie die Koordinaten eines Punktes $D$ , der von der Ebene $E$ den Abstand $d = \sqrt{10}$ LE besitzt.
3
Die Abbildung zeigt ein Prisma, bei dem die beiden parallelen und deckungsgleichen Trapeze $A B F E$ und $D C G H$ senkrecht auf der Grundfläche $A B C D$ stehen.
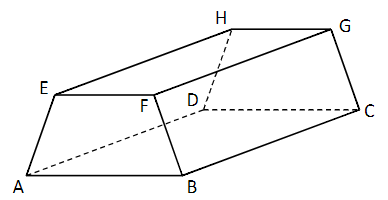
1. Nehmen Sie Stellung zu folgender Aussage:
  „Das Volumen des Prismas berechnet sich mittels der Formel $V = | \vec{A D} \circ (\vec{A E} \times \vec{A B}) |$ ".
2. Begründen Sie anhand des beschriebenen Prismas, wie viele Lösungen die Gleichung $λ_{1} \cdot \vec{A B} + λ_{2} \cdot \vec{A D} + λ_{3} \cdot \vec{H G} = \vec{0}$ mit den Unbekannten $λ_{1}, λ_{2}, λ_{3} \in ℝ$
  besitzt.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?