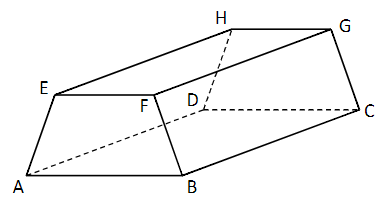
Nehmen Sie Stellung zu folgender Aussage:

„Das Volumen des Prismas berechnet sich mittels der Formel $V=\mid \overrightarrow{AD}\circ (\overrightarrow{AE}\times \overrightarrow{AB})\mid V=\backslash left|\; \backslash overrightarrow\{AD\}\backslash circ\; (\backslash overrightarrow\{AE\}\backslash times\; \backslash overrightarrow\{AB\})\backslash right|$ ".

Begründen Sie anhand des beschriebenen Prismas, wie viele Lösungen die Gleichung ${\lambda }_1\cdot \overrightarrow{AB}+{\lambda }_2\cdot \overrightarrow{AD}+{\lambda }_3\cdot \overrightarrow{HG}=\overrightarrow{0}\backslash lambda\_1\backslash cdot\; \backslash overrightarrow\{AB\}+\backslash lambda\_2\backslash cdot\; \backslash overrightarrow\{AD\}+\backslash lambda\_3\backslash cdot\; \backslash overrightarrow\{HG\}=\backslash overrightarrow0$ mit den Unbekannten ${\lambda }_1,{\lambda }_2,{\lambda }_3\in \mathbb{R}\backslash lambda\_1,\; \backslash lambda\_2,\; \backslash lambda\_3\; \backslash in\; \backslash mathbb\{R\}$

besitzt.